The %MktPPro Macro

Introduction

The %MktPPro autocall macro makes optimal partial-profile designs from block designs and orthogonal arrays.

An incomplete block design is a list of $t$ treatments that appear together in $b$ blocks. Each block contains a subset ( $k < t$ ) of the treatments. An unbalanced block design is an incomplete block design in which every treatment appears with the same frequency, but pairwise frequencies (the number of times each treatment appears with each other treatment in a block) are not constant. When both treatment and pairwise frequencies are constant, the design is a balanced incomplete block design (BIBD). You can make optimal partial-profile designs with BIBDs (the best) and also with unbalanced block designs. Although you can more generally use any incomplete block design, the results are not usually optimal.

%MktPPro Macro Syntax

%MktPPro(IBD=SAS-data-set | X=SAS-data-set <, optional arguments>)

Required Arguments

You must specify either IBD= or X= but not both.

IBD=SAS-data-set: specifies the block design. Ideally, this design is a BIBD, but an unbalanced block design is acceptable. Also, you can use any incomplete block design.
X=SAS-data-set: specifies the incidence matrix for the block design, which is a binary coding of the design.

Optional Arguments

DESIGN=SAS-data-set

specifies the orthogonal array from the %MktEx macro.

OUT=SAS-data-set

specifies the output choice design.

PRINT=print-options

specifies both of the output display options. You can specify one or more of the following:

I: specifies incomplete block design.
F: specifies a crosstabulation of attribute frequencies.
P: specifies a partial-profile design.

By default, PRINT=F.

Help Option

You can specify either of the following to display the option names and simple examples of the macro syntax:

%mktppro(help)
%mktppro(?)

%MktPPro Macro Notes

This macro specifies options nonotes throughout most of its execution. If you want to see all the notes, submit the following statement before running the macro:

%let mktopts = notes;

To see the macro version, submit the following statement before running the macro:

%let mktopts = version;

Example

In a certain class of partial-profile designs, a block design specifies which attributes vary in each choice set, and an orthogonal array specifies how the attributes vary. This example makes an optimal partial-profile choice design that has 16 binary attributes, four of which vary at a time in 80 choice sets. The following statements create and evaluate the partial-profile design:

%mktex(4 2 ** 4, n=8, seed=306)

proc sort data=randomized out=randes(drop=x1);
   by x2 x1;
   run;

proc print noobs data=randes;
run;

%mktbibd(b=20, nattrs=16, setsize=4, seed=104)

%mktppro(design=randes, IBD=bibd, print=f p)

%choiceff(data=chdes,                 /* candidate set of choice sets         */
          init=chdes,                 /* initial design                       */
          initvars=x1-x16,            /* factors in the initial design        */
          model=class(x1-x16 / sta),  /* model with stdz orthogonal coding    */
          nsets=80,                   /* number of choice sets                */
          nalts=2,                    /* number of alternatives               */
          rscale=                     /* relative D-efficiency scale factor   */
          %sysevalf(80 * 4 / 16),     /* 4 of 16 attrs in 80 sets vary        */
          beta=zero)                  /* assumed beta vector, Ho: b=0         */

The results of these steps are shown after some more explanation of the process of making a partial-profile choice design by using this method. Two input designs are input to the %MktPPro macro. The first is an orthogonal array. The orthogonal array must be a $p^ k$ subset of an array $p^ k s^1$ in $p \times s$ runs where $k \le s$ . The following designs are examples of suitable orthogonal arrays:

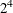$2^4$ in 8 runs, selected from 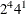$2^4 4^1$ in 8 runs
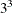$3^3$ in 9 runs, selected from 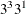$3^3 3^1$ in 9 runs
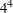$4^4$ in 16 runs, selected from 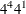$4^4 4^1$ in 16 runs
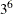$3^6$ in 18 runs, selected from 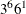$3^6 6^1$ in 18 runs

You can use the %MktOrth or %MktRuns macro to see whether the orthogonal array of interest exists. The following statements list the arrays that work:

%mktorth(options=parent, maxlev=144)

data x(keep=n design);
   set mktdeslev;
   array x[144];
   c = 0;
   one = 0;
   k = 0;
   do i = 1 to 144;
      c + (x[i] > 0);
      if x[i] > 1 then do;
         p = i;
         k = x[i];
      end;
      if x[i] = 1 then do;
         one + 1;
         s = i;
      end;
   end;
   if c = 1 then do;
      c = 2;
      one = 1;
      s = p;
      k = p - 1;
   end;
   if c = 2 and one = 1 and k > 2 and s * p = n;
   design = compbl(left(design));
   run;

proc print;
run;

The rows of the orthogonal array must be sorted into the right order. Each submatrix of $s$ rows in this kind of orthogonal array is called a difference scheme, and submatrices 2 through $p$ are obtained from the preceding submatrix by adding 1 (in the appropriate Galois field). You do not get the right results if you use any other kind of orthogonal array.

There are several ways to create an orthogonal array that is sorted in the right way. The preceding %MktEx macro step requests the $s$ -level factor first, and then sorts the randomized design by the first $p$ -level factor followed by the $s$ -level factor. Finally, it discards the $s$ -level factor. Alternatively, you could first request one of the $p$ -level factors, then request the $s$ -level factor, and then request the remaining $(k-1)$ $p$ -level factors. Then, you could discard the $s$ -level factor x2 from the OUT=Design data set after the array is created. You cannot drop the second factor in the %MktEx macro step by specifying OUT=Design(DROP=x2), because the %MktEx macro will drop the variable and then sort, and your rows will be in the wrong order. The former approach has the advantage of being less likely to produce alternatives that are constant (that is, in one alternative all attributes are absent, and in other alternatives all attributes are present).

The orthogonal array is as follows:

                              x2    x3    x4    x5

                               1     1     2     1
                               1     2     2     2
                               1     1     1     2
                               1     2     1     1
                               2     2     1     2
                               2     1     1     1
                               2     2     2     1
                               2     1     2     2

The second input data set contains the block design. In the preceding example, the BIBD is as follows:

                        Balanced Incomplete Block Design

                              x1    x2    x3    x4

                              15    16     5     6
                               4     1    16    12
                               5    13     4     7
                               9     4     6     8
                              14     8    13    16
                              12    14     5    10
                              13     9    12     3
                               7     8     1    10
                              16     7     3    11
                               8    12    11    15
                              10     3    15     4
                               1     6     3    14
                               2    11     4    14
                              15     7    14     9
                               6     2     7    12
                              11     5     9     1
                              13    15     2     1
                              16    10     9     2
                              11     6    10    13
                               3     2     8     5

This design has B=20 rows, so the final choice design will have 20 blocks of choice sets (in this case 20 blocks of 4 choice sets). The number of attributes is $t=16$ , which is specified by NATTRS=16. The number of attributes in each block is specified by SETSIZE=4. This design specifies that in the first block of $s=4$ choice sets, attributes 15, 16, 5, and 6 will vary; in the second block of 4 choice sets, attributes 4, 1, 16, and 12 will vary; and so on. Alternative $i$ = 1, $\ldots$ , $p$ , in each block of $s$ choice sets is made from a submatrix of $s$ runs in the orthogonal array. For example, alternative 1 of the first $s$ choice sets is made from the first $s$ runs in the orthogonal array, alternative 2 is made from the next $s$ runs in the orthogonal array, and so on. Each attribute should appear the same number of times in the block design. The following t=16 by t=16 attribute frequencies matrix shows how often each attribute appears with every other attribute in our design:

                       Attribute by Attribute Frequencies

                   1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16

                1  5  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
                2     5  1  1  1  1  1  1  1  1  1  1  1  1  1  1
                3        5  1  1  1  1  1  1  1  1  1  1  1  1  1
                4           5  1  1  1  1  1  1  1  1  1  1  1  1
                5              5  1  1  1  1  1  1  1  1  1  1  1
                6                 5  1  1  1  1  1  1  1  1  1  1
                7                    5  1  1  1  1  1  1  1  1  1
                8                       5  1  1  1  1  1  1  1  1
                9                          5  1  1  1  1  1  1  1
               10                             5  1  1  1  1  1  1
               11                                5  1  1  1  1  1
               12                                   5  1  1  1  1
               13                                      5  1  1  1
               14                                         5  1  1
               15                                            5  1
               16                                               5

Each attribute appears five times and is paired with every other attribute exactly once. The fact that values above the diagonal are constant indicates that this block design is a BIBD. The number of choice sets is $s$ times the number of blocks (rows in the design), in this case, $4 \times 20 = 80$ . The number of attributes is the maximum value in the BIBD (NATTRS=t=16). The number of attributes that vary at any one time is SETSIZE= $k \le s$ . All factors have $p$ levels, and all choice sets have $p$ alternatives. The final report from the %ChoicEff macro is as follows:

                                 Final Results

                           Design                  1
                           Choice Sets            80
                           Alternatives            2
                           Parameters             16
                           Maximum Parameters     80
                           D-Efficiency      20.0000
                           Relative D-Eff   100.0000
                           D-Error            0.0500
                           1 / Choice Sets    0.0125



                   Variable                               Standard
              n      Name      Label    Variance    DF      Error

              1      x11       x1 1       0.05       1     0.22361
              2      x21       x2 1       0.05       1     0.22361
              3      x31       x3 1       0.05       1     0.22361
              4      x41       x4 1       0.05       1     0.22361
              5      x51       x5 1       0.05       1     0.22361
              6      x61       x6 1       0.05       1     0.22361
              7      x71       x7 1       0.05       1     0.22361
              8      x81       x8 1       0.05       1     0.22361
              9      x91       x9 1       0.05       1     0.22361
             10      x101      x10 1      0.05       1     0.22361
             11      x111      x11 1      0.05       1     0.22361
             12      x121      x12 1      0.05       1     0.22361
             13      x131      x13 1      0.05       1     0.22361
             14      x141      x14 1      0.05       1     0.22361
             15      x151      x15 1      0.05       1     0.22361
             16      x161      x16 1      0.05       1     0.22361
                                                    ==
                                                    16

The variances are constant, and the relative D-efficiency is 100. D-efficiency is 20, which is 4/16 of the number of choice sets, 80. Because 25% of the attributes vary, D-efficiency is 25% of what you expect in a full-profile generic choice design. RSCALE=20 is specified so that relative D-efficiency can be based on the true maximum. The macro function %SYSEVALF is used to evaluate the expression $80 * 4 / 16$ to get the 20. This function evaluates expressions that contain or produce floating-point numbers and then returns the result. In summary, this design is optimal for partial profiles, and it is 25% efficient relative to an optimal generic design in which all attributes can vary.

The first three choice sets are as follows:

   Set  x1  x2  x3  x4  x5  x6  x7  x8  x9  x10  x11  x12  x13  x14  x15  x16

     1   1   1   1   1   2   1   1   1   1   1    1    1    1    1    1    1
         1   1   1   1   1   2   1   1   1   1    1    1    1    1    2    2

     2   1   1   1   1   2   2   1   1   1   1    1    1    1    1    1    2
         1   1   1   1   1   1   1   1   1   1    1    1    1    1    2    1

     3   1   1   1   1   1   2   1   1   1   1    1    1    1    1    1    1
         1   1   1   1   2   1   1   1   1   1    1    1    1    1    2    2

The choice design is statistically optimal, but it might not be optimal from the standpoint of practical usage. In every choice set, there is a pair of alternatives: one with three attributes present and one with only one attribute present. This might not meet your needs. You always need to inspect your designs to see how well they work for your purposes. Statistical efficiency and optimality are just one part of the picture. With the OA $4^1 2^4$ in eight runs, there is one other kind of OA that you can get by specifying other random number seeds, which always produces a choice set (one in each block of choice sets) where all four attributes are present in one alternative and none are present in the other alternative. This might be worse. This kind of problem is less likely to be an issue when you vary more than four attributes.

You can make an optimal partial-profile choice design by using an unbalanced block design (instead of a BIBD). In an unbalanced block design, the treatment frequencies are constant, but the pairwise frequencies are not constant. The following example makes a design with six 3-level factors in 60 choice sets with three alternatives each:

%mktex(6 3 ** 6, n=18, seed=424)

proc sort data=randomized out=randes(drop=x1);
   by x2 x1;
run;

proc print data=randes noobs;
run;

%mktbsize(nattrs=20, setsize=6, options=ubd)

%mktbibd(b=10, nattrs=20, setsize=6, seed=104)

%mktppro(design=randes, IBD=bibd, print=f p)

%choiceff(data=chdes,                /* candidate set of choice sets         */
          init=chdes,                /* initial design                       */
          initvars=x1-x20,           /* factors in the initial design        */
          model=class(x1-x20 / sta), /* model with stdz orthogonal coding    */
          nsets=60,                  /* number of choice sets                */
          nalts=3,                   /* number of alternatives               */
          rscale=                    /* relative D-efficiency scale factor   */
          %sysevalf(60 * 6 / 20),    /* 6 of 20 attrs in 60 sets vary        */
          beta=zero)                 /* assumed beta vector, Ho: b=0         */

The %MktBSize macro is used to suggest the size of a block design. Each attribute appears three times in the design, and each pair occurs in the range 0 to 2 times (average 0.79). The design is optimal for this specification.

The D-efficiency is 18, which corresponds to the 6/20 of 60 choice sets, and the relative D-efficiency is 100. This shows that the design is optimal for partial profiles and is 30% efficient relative to a full-profile optimal generic design where all attributes can vary.

You could also specify B=20 in the %MktBIBD macro and NSETS=120 in the %ChoicEff macro to make larger designs. Any integer multiple of B=10 will work.

FOCUS AREAS