FOCUS AREAS
Contents | SAS Program | PDF

The %MktMDiff Macro

Introduction

The %MktMDiff autocall macro analyzes MaxDiff (maximum difference or best-worst) data. In a MaxDiff study, subjects are shown sets of messages or product attributes and are asked to choose the best (or most important) from each choice set and also the worst (or least important). The design consists of the following:

  • $t$ attributes

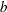  • $b$ choice sets (blocks) of attributes

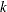  • $k$ attributes in each choice set (block)

These are the parameters of a balanced incomplete block design (BIBD), which you can construct by using the %MktBIBD macro. You can also use designs that do not meet the strict requirements of a BIBD.

To use the macro, you provide two data sets. One data set contains the experimental design. The other data set contains the subjects’ response data. You must specify arguments that identify the number of attributes in the design, the number of choice sets (blocks) in the design, and the number of attributes in each choice set (block). Finally, you must specify an argument that identifies the layout of the subjects’ response data. The %MktMDiff macro reads the experimental design data set and the response data set, and then combines and arranges the two data sets in the proper form for analysis. The data are arrayed so that each original MaxDiff choice set forms two choice sets in the analysis: one positively weighted set for the best choice and one negatively weighted set for the worst choice. The macro then performs the analysis by using PROC PHREG to fit a multinomial logit model. The result of the analysis is a scaling of the attributes on a preference or importance scale.

The Subjects’ Response Data

The subjects’ response data can be in one of the following eight forms:

BW

best then worst (for example, b1–b18 w1–w18), and the data are attribute numbers (ranging from 1 to NATTRS=$t$).

WB

worst then best (for example, w1–w18 b1–b18), and the data are attribute numbers (ranging from 1 to NATTRS=$t$).

BWALT

best then worst and alternating (for example, b1 w1 b2 w2 $\ldots $ b18 w18), and the data are attribute numbers (ranging from 1 to NATTRS=$t$).

WBALT

worst then best and alternating (for example, w1 b1 w2 b2 $\ldots $ w18 b18), and the data are attribute numbers (ranging from 1 to NATTRS=$t$).

BWPOS

best then worst (for example, b1–b18 w1–w18), and the data are positions (ranging from 1 to SETSIZE=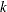$k$).

WBPOS

worst then best (for example, w1–w18 b1–b18), and the data are positions (ranging from 1 to SETSIZE=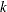$k$).

BWALTPOS

best then worst and alternating (for example, b1 w1 b2 w2 $\ldots $ b18 w18), and the data are positions (ranging from 1 to SETSIZE=$k$).

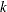WBALTPOS

worst then best and alternating (for example, w1 b1 w2 b2 $\ldots $ w18 b18), and the data are positions (ranging from 1 to SETSIZE=$k$).

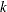Any variable names can be used. For example, the variables could be x1–x36. In the case of BWALT, the odd-numbered variables will correspond to best picks and the even-numbered variables will correspond to worst picks.

%MktMDiff Macro Syntax

%MktMDiff( layout, DESIGN=, NATTRS=, NSETS=, SETSIZE= <, optional arguments>)

Required Arguments

layout

specifies a positional argument that indicates the structure of the choice data. You must specify this argument first. Specify only a value, not LAYOUT=. The value has several components, you can use lowercase or uppercase, and spaces between the components are optional. The values are B, W, ALT, and POS. You must specify both a B and a W. When B comes before W, the best variables come before the worst variables. Otherwise, when W comes before B, the worst variables come before the best variables. You can optionally specify ALT as well, which means that the variables alternate (for example, b1 w1 b2 w2 b3 w3, where the B variables are the best variables and the W variables are the worst variables). Otherwise, it is expected that all of one type appear, then all of the other type. By default, the data are assumed to be the numbers of the attributes that were chosen (for example, 1 to 6 when there are a total of NATTRS=6 attributes). If instead (for example, with SETSIZE=3), the data are 1 to 3, indicating the position of the chosen attribute, then you must specify POS as well.

For example:

BW | B W

indicates best then worst; for example, b1–b6 w1–w6 or even x1–x12 (if $2 \times b = 12$). The order of the values needs to be best then worst. The data are attribute numbers.

WB | W B

indicates worst then best; for example, w1–w6 b1–b6 or even x1–x12 (if $2 \times b = 12$). The order of the values needs to be worst then best. The data are attribute numbers.

BWALT | B W ALT | ALT B W

indicates best then worst and alternating; for example, b1 w1 b2 w2 $\ldots $ or even x1–x12 (if $2 \times b = 12$). The order of the values must alternate: best then worst. The data are attribute numbers.

WBALT |W B ALT | ALT W B

indicates worst then best and alternating; for example, w1 b1 w2 b2 $\ldots $ or even x1–x12 (if $2 \times b = 12$). The order of the values must alternate: worst then best. The data are attribute numbers.

BWPOS | B W ALT | B POS W

indicates best then worst, and the data are positions.

WBPOS | W B POS | W POS B

indicates worst then best, and the data are positions.

BWALTPOS | B W ALT POS | ALT B POS W

indicates best then worst and alternating, and the data are positions.

WBALTPOS | W B ALT POS | ALT W POS B

indicates worst then best and alternating, and the data are positions.

DESIGN=SAS-data-set

specifies the data set along with the design. The design is usually a BIBD in the format that is produced by the OUT= argument of the %MktBIBD macro. All numeric variables are assumed to contain the BIBD, unless there is exactly one extra variable, and the first or last variable is called Group. In that case, the group variable is ignored.

NATTRS=t
T=t

specifies the number of attributes or messages. The "T" in T= stands for treatments and corresponds to typical BIBD notation.

NSETS=b
B=b

specifies the number of sets. The "B" in B= stands for blocks and corresponds to typical BIBD notation.

SETSIZE=k
K=k

specifies the number of attributes or messages that are shown at one time (in a set). The K= argument is named using typical BIBD notation.

Optional Arguments

Data Set Arguments
DATA=SAS-data-set

specifies the input data set. By default, the last data set that is created is used.

OUT=SAS-data-set

specifies the output data set in a form ready for coding. By default, OUT=MaxDiff.

OUTCODED=SAS-data-set

specifies the output data set that has been coded by PROC TRANSREG. By default, OUTCODED=Coded.

OUTPARM=SAS-data-set

specifies the output data set along with the parameter estimates table. By default, OUTPARM=ParmEst. If the RESCALE= argument is specified, the requested results are added to this data set.

Other Arguments
ATTRS=macro-variable

specifies the name of a macro variable that contains a comma-delimited list of the attribute descriptions from the study. For example, in a cell phone choice example, you can store your attributes as a comma-delimited list in a macro variable as follows: 

%let attrlist=Camera,Flip,Hands Free,Games,Internet
,Free Replacement,Battery Life,Large Letters,Applications;

Then you would specify the argument: ATTRS=attrlist. Alternatively, after the name you can specify a single nonblank delimiter character to use instead of a comma (if you need to include commas in the attribute descriptions).

For example, ATTRS=Myattrs - (using a dash as a delimiter). If you do not specify this argument, the default attribute names are "A1", "A2", and so on. The macro variable must have a name that does not match any of the macro parameter names (for example, you cannot specify ATTRS=Attrs). The name also must not match any macro names that the macro uses internally. In the unlikely event that you specify an invalid name, an error message is displayed. Most names, including any name that contains 'Att' that is not 'Attrs' or 'Nattrs', are always going to work.

CLASSOPTS=options-list

specifies options to apply to the classification variable; for example, CLASSOPTS=EFFECTS. The classification variable in the final analysis data set contains the descriptions of the attributes that are specified in the ATTRS= macro variable. By default, CLASSOPTS=ZERO=NONE. A reference cell coding is used, and the reference level is displayed with a parameter estimate of 0. If you specify a null value (CLASSOPTS=), then the default reference cell coding is used and the reference level is not displayed. You can control the reference level by specifying CLASSOPTS=ZERO=reference-level and naming the appropriate reference level. The reference level will exactly match one of the descriptions in the ATTRS= macro variable.

GROUP=g

specifies the number of blocks of choice sets. By default, when this argument is not specified, it is assumed that the design consists of one big group. Otherwise, when you have n subjects in each group and GROUP=g, there are $n \times g$ rows of data, each consisting of $b / g$ best values and $b / g$ worst values. The number of subjects in each group must be the same. It is also assumed that the design is sorted by the group variable. If the design is made by the %MktBIBD macro, this will always be the case. If the DESIGN= data set has $k+1$ variables and either the first variable or the last variable is called Group (case is ignored), then that variable is ignored and not treated as part of the design. Otherwise, the DESIGN= data set is required to have $k$ variables.

OPTIONS=options-list

specifies binary arguments. You can specify one or more of the following values:

NOCODE

creates the OUT= data set but does not code or do the analysis.

NOANALYSIS

creates the OUT= and OUTCODED= data sets but does not do the analysis.

NOSORT

does not sort the parameter estimates table by the parameter estimates.

NODROP

does not drop the variable or parameter column from the parameter estimates table.

RESCALE

ignores the usual restriction that the RESCALE= argument can be used only in the context of the default CLASSOPTS= argument. If you specify this argument, you must ensure that you are using only the ZERO= argument to change the reference level or are otherwise doing something that will not change the coding from reference cell to something else.

By default, none of these arguments are specified.

RESCALE=value

specifies various ways to rescale the parameter estimates. You can specify the following values:

ADJUSTED
ADJ

adjusts parameter estimates by the number of attributes in each set. First, $\hat{\bbeta }$ is centered and then scaled as follows:

\[ \frac{\exp (\hat{\beta }_ i)}{\exp (\hat{\beta }_ i) + k - 1} \]

Finally, the adjusted values are rescaled to sum to 1.

ADJUSTED100
ADJ100

adjusts parameter estimates by the number of attributes in each set. First, $\hat{\bbeta }$ is centered and then scaled as follows:

\[ \frac{\exp (\hat{\beta }_ i)}{\exp (\hat{\beta }_ i) + k - 1} \]

Finally, the adjusted values are rescaled to sum to 100.

ALL

reports the default and all rescaled values.

CENTER

centers parameter estimates.

DEFAULT

produces ordinary parameter estimates.

P

scales parameter estimates to probabilities:

\[ \frac{\exp (\hat{\beta }_ i)}{\sum _{j=1}^{m} \exp (\hat{\beta }_ j)} \]
P100

scales parameter estimates to probabilities and then multiplies them by 100:

\[ \frac{100 \exp (\hat{\beta }_ i)}{\sum _{j=1}^{m} \exp (\hat{\beta }_ j)} \]

Note that RESCALE= and RESCALE=DEFAULT are equivalent. When this argument is specified (or any argument besides RESCALE=DEFAULT is specified), an additional table is displayed that shows the rescaled parameter estimates. You can specify multiple values and get multiple columns in the results table; for example, RESCALE=DEFAULT ADJ100. All specified rescalings are added to the OUTPARM= data set. These rescalings were suggested by Sawtooth Software (2005, 2007).

Do not use both the RESCALE= argument and the CLASSOPTS= argument unless you are only changing details of the reference cell coding. If you use these arguments together, you must ensure that you are using only the ZERO= argument to change the reference level or are otherwise doing something that will not change the coding from reference cell to something else. In that case, you can specify OPTIONS=RESCALE to allow the analysis to proceed.

VARS=variable-list

specifies the variables in the DATA= data set that contain the data. There must be $2 \times b$ variables in this list (from NSETS=$b$). The default is all numeric variables in the data set.

Help Argument

You can specify either of the following to display the option names and simple examples of the macro syntax: 

%mktmdiff(help)
%mktmdiff(?)

%MktMDiff Macro Notes

This macro specifies options nonotes throughout most of its execution. If you want to see all the notes, submit the following statement before running the macro: 

%let mktopts = notes;

To see the macro version, submit the following statement before running the macro: 

%let mktopts = version;

Example

A researcher is interested in preference for cell phones based on the attributes of the phones. The attributes are as follows:

Camera

Flip

Hands Free

Games

Internet

Free Replacement

Battery Life

Large Letters

Applications

Subjects are shown subsets of these nine attributes and asked to pick which is the most important when they choose a cell phone and which is the least important. You can use the %MktBSize autocall macro as follows to get ideas about how many blocks to use and how many to show at one time: 

%mktbsize(nattrs=9, setsize=2 to 9, nsets=1 to 20)

Figure 1 displays the results.

Figure 1: %MktBSize Output


t
Number of
Attributes
k
Set
Size
b
Number
of Sets
r
Attribute
Frequency
Lambda
Pairwise
Frequencies
n
Total
Sample
Size
9 3 12 4 1 36
9 4 18 8 3 72
9 5 18 10 5 90
9 6 12 8 5 72
9 8 9 8 7 72 



 
With nine attributes, there are five sizes that meet the necessary but not sufficient conditions for the existence of a BIBD. Of the candidates (3, 4, 5, 6, and 8), 4 or 5 seem like good choices. (Three seems a bit small and more than 5 seems a bit big, given that you have only 9 attributes.) The following statement creates a BIBD that has T=9 attributes, shown in B=18 sets of size K=5: 
%mktbibd(nattrs=9, setsize=5, nsets=18, seed=377, out=sasuser.bibd)

Figure 2 shows the attribute by attribute frequency matrix of the design. 
  
Figure 2: Attribute by Attribute Frequencies









Attribute by Attribute Frequencies

















 
1
2
3
4
5
6
7
8
9

1
10
5
5
5
5
5
5
5
5

2
.
10
5
5
5
5
5
5
5

3
.
.
10
5
5
5
5
5
5

4
.
.
.
10
5
5
5
5
5

5
.
.
.
.
10
5
5
5
5

6
.
.
.
.
.
10
5
5
5

7
.
.
.
.
.
.
10
5
5

8
.
.
.
.
.
.
.
10
5

9
.
.
.
.
.
.
.
.
10










 
The diagonal elements of the matrix show how often each attribute occurs. Each of the T=9 attributes occurs the same number of times (10 times). Furthermore, each of the T=9 attributes occurs with each of the remaining eight attributes exactly 5 times. These two constant values, one on the diagonal and one off the diagonal, show that the design is a BIBD. 
Figure 3 shows the design. 
  
Figure 3: BIBD Design





Balanced Incomplete Block Design






x1
x2
x3
x4
x5

1
2
4
7
9

6
2
9
8
4

5
8
2
1
7

7
9
1
6
3

9
7
6
5
2

3
1
5
6
8

4
6
3
8
2

6
7
4
1
8

7
5
2
3
4

1
3
8
2
7

3
4
1
5
9

2
9
6
3
1

8
3
9
2
5

9
8
7
4
3

5
4
8
9
1

2
1
5
4
6

8
5
7
9
6

4
6
3
7
5










 
The first choice set consists of attributes 1, 2, 4, 7, and 9, which correspond to the following: 



     



       
 Camera 


     



       
Flip 


     



       
Games 


     



       
Battery Life 


     



       
Applications 


     



Subjects choose the best and worst from this and every other set. 
The following DATA step creates the subjects’ response data set: 
title 'Best Worst Example with Cell Phone Attributes';

data bestworst;
  input Sub $ @4 (b1-b18 w1-w18) (1.);
  datalines;
 1 188661884399349653941955342212935494
 2 765358873891388493922673644336595554
 3 782126282892848564995993447213935655
 4 481363264246399187162125415351281453
 5 787168863811878175225995382352235293
 6 787658867891878667495965442313345453
 7 788171867736888187465395344393344453
 8 788771867711888687445353445353335254
 9 188778887896878687425323443242344454
10 788778887816888687445353444343344454
11 787778877816878667442353343343235453
12 787778387711898667425321443253544594
13 767668285791988687441951364232234194
14 187168877741878687445323445216334453
15 788176487116988675492393314339579457
16 267665615733884677442193342349545564
17 481191867813938266147956244139584594
18 725778814832585185141193643296944467
19 188678863811279263445123344253934596
20 728698612719281483265755285851944597
;

Next, the descriptions of each of the t attributes are listed in comma-delimited form and stored in the macro variable &attrlist.
Note: When the list is split across lines, care is taken to ensure that the next attribute description, "Free Replacement," immediately follows the comma so that it will not begin with a leading blank. 
%let attrlist=Camera,Flip,Hands Free,Games,Internet
,Free Replacement,Battery Life,Large Letters,Applications;

Now you can use the %PHChoice autocall macro to customize the output from PROC PHREG, which the %MktMDiff macro calls, to look like the output from a discrete choice procedure instead of a survival analysis procedure: 
%phchoice( on )

Finally, you invoke the %MktMDiff macro as follows: 
%mktmdiff(bw, nattrs=9, nsets=18, setsize=5, attrs=attrlist,
          data=bestworst, design=sasuser.bibd)

The %MktMDiff macro call begins with a positional parameter that specifies the layout of the data. The BW specification indicates that the data are best then worst, the variables do not alternate, and the data are attribute numbers. The NSETS= argument specifies that there are 18 choice sets. The NATTRS= argument specifies that there are nine attributes. SETSIZE=5 specifies that there are five attributes in each choice set. The ATTRS= argument specifies that the macro variable &attrlist contains a list of the attributes. However, you specify the macro variable name attrlist and not the value of the variable &attrlist. The DATA= argument specifies that the data set BestWorst contains the subjects’ responses. The DESIGN= argument specifies that the data set Sasuser.bibd contains the design. 
The %MktMDiff macro begins by displaying the summary of the input as shown in Figure 4. 
  
Figure 4: %MktMDiff Summary of Input Data





Best Worst Example with Cell Phone Attributes








Var Order:   Best then Worst
Alternating: Variables Do Not Alternate
Data:        Attribute Numbers (Not Positions)
Best Vars:   b1 b2 b3 b4 b5 b6 b7 b8 b9 b10 b11 b12 b13 b14 b15 b16 b17 b18
Worst Vars:  w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 w13 w14 w15 w16 w17 w18
Attributes:  Camera
             Flip
             Hands Free
             Games
             Internet
             Free Replacement
             Battery Life
             Large Letters
             Applications










 
The data consist of the best variables and then the worst variables. The best variables are b1–b18, and the worst variables are w1–w18. The data are attribute numbers (1 to T=9), not positions (1 to K=5). Finally, the descriptions of each of the $t$ attributes are listed. 
The table in Figure 5 is of interest as a check of the integrity of the input data. 
  
Figure 5: Summary of Subjects, Sets, and Chosen and Unchosen Alternatives









Summary of Subjects, Sets, and Chosen and
Unchosen Alternatives		

Pattern
Number of
Choices		
Number of
Alternatives		
Chosen
Alternatives		
Not Chosen

1
36
100
20
80










 
In the aggregate data set, there is one pattern of input, which occurs 36 times (18 best choices per subject plus 18 worst choices). There are 100 alternatives (5 attributes in a set examined by 20 individuals); each of the 20 subjects chose 1 ($20 \times 1 = 20$) and did not choose 4 ($20 \times 4 = 80$). 
Figure 6 shows the multinomial logit parameter estimates. 
  
Figure 6: Parameter Estimates





Best Worst Example with Cell Phone Attributes






Multinomial Logit Parameter Estimates

 
DF
Parameter
Estimate		
Standard
Error		
Chi-Square
Pr > ChiSq

Large Letters
0
0
.
.
.

Battery Life
1
-0.52009
0.17088
9.2635
0.0023

Free Replacement
1
-1.01229
0.17686
32.7598
<.0001

Camera
1
-1.30851
0.18232
51.5096
<.0001

Applications
1
-1.93107
0.18741
106.1680
<.0001

Flip
1
-2.00892
0.18788
114.3334
<.0001

Internet
1
-2.44592
0.18731
170.5156
<.0001

Hands Free
1
-2.47063
0.18781
173.0569
<.0001

Games
1
-2.86329
0.18802
231.9065
<.0001










 
The parameter estimates are arranged from most preferred to least preferred. These results are also available in a SAS data set called ParmEst. 
You could change the reference level by using the CLASSOPTS= argument as follows: 
%mktmdiff(bw, nattrs=9, nsets=18, setsize=5,
     attrs=attrlist, classopts=zero='Internet',
     data=bestworst, design=sasuser.bibd)

Figure 7 shows the new parameter estimates. 
  
Figure 7: Parameter Estimates





Best Worst Example with Cell Phone Attributes






Multinomial Logit Parameter Estimates

 
DF
Parameter
Estimate		
Standard
Error		
Chi-Square
Pr > ChiSq

Large Letters
1
2.44592
0.18731
170.5156
<.0001

Battery Life
1
1.92583
0.18533
107.9789
<.0001

Free Replacement
1
1.43363
0.18658
59.0424
<.0001

Camera
1
1.13741
0.18484
37.8650
<.0001

Applications
1
0.51485
0.18056
8.1305
0.0044

Flip
1
0.43700
0.18045
5.8650
0.0154

Hands Free
1
-0.02471
0.17655
0.0196
0.8887

Games
1
-0.41737
0.17375
5.7702
0.0163










 
The parameter estimates have all changed by a constant amount. You get the new estimates by taking the original estimate for the internet parameter and subtracting it from all the original estimates.