The %MktEx Macro

Introduction

The %MktEx autocall macro creates efficient factorial designs. It can handle simple problems like main-effects designs and more complicated problems, including designs that have interactions and restrictions on which levels can appear together. For most simple problems, you need to specify only the levels of all the factors and the number of runs. For more complicated problems, you might also need to specify the interactions that you want to estimate or any restrictions that you want to impose on the design.

The macro uses a variety of methods and works iteratively as it attempts to optimize the D-efficiency of the design. As D-efficiency increases, the standard errors of the parameter estimates in the linear model decrease. A perfect design is orthogonal and balanced and has 100% D-efficiency. A design is orthogonal when all the parameter estimates are uncorrelated. A design is balanced when all the levels within each of the factors occur equally often. A design is orthogonal and balanced when the variance matrix, which is proportional to ${(\bX ’\bX )}^{-1}$ , is diagonal, where $\bX$ is a suitable orthogonal coding of the design matrix.

By default, the %MktEx macro creates the following output data sets to contain the final design:

OUT=Design, the experimental design, sorted by the factor levels
OUTR=Randomized, the randomized experimental design

The two designs are equivalent and have the same D-efficiency. The OUT=Design data set is sorted and is usually easier to inspect visually; however, the OUTR=Randomized design is usually the better one to use. The randomized design has rows that are sorted in random order and factor levels that are randomly reassigned.

%MktEx Macro Syntax

%MktEx( list, N=n, <, optional arguments>)

Required Arguments

list

specifies a list of the numbers of levels of all the factors. For example, suppose you want a design that has two 2-level factors, two 3-level factors, and two 4-level factors. You can specify a list of the form 2 2 3 3 4 4, where a number is provided for each factor. You can also use the shorthand notation 2**2 3**2 4**2, where the number that precedes the ** indicates the number of levels of a factor and the number that follows the ** indicates the number of factors that have that particular number of levels. The two types of notation can also be combined, as in 2 2 3**2 4 4. The factor list is a positional argument, meaning that when it is specified, it must come first. Unlike all other arguments, it is not specified after a name and an equal sign.

You have to specify a list for most designs, but in some cases you can specify only the N= argument and omit the list, and a default list is implied. For example, N=18 implies a list of 2 3**7. When there are no interactions, restrictions, or duplicate exclusions, and the list is omitted, then by default there are no PROC OPTEX iterations (OPTITER=0).

N=n

specifies the number of runs in the design. You can use the %MktRuns macro to get suggestions for values of N=.

Optional Arguments

Basic Arguments

The following are the most commonly used arguments.

BALANCE=d

specifies the maximum allowable level-frequency range. That is, BALANCE=d specifies that for each factor, a difference between the frequencies of the most and least frequently occurring levels should be no greater than d. Specify a positive integer (usually 1 or 2) that indicates an acceptable degree of imbalance. By default, no balance restrictions are added.

The BALANCE= argument works by adding restrictions to the design. The badness of each column (how far each column is from conforming to the balance restrictions) is evaluated, and the results are stored in a scalar named __bbad. When you specify other restrictions, the value that is stored in __bbad is added to the variable Bad, which is created by your restrictions macro. You can use your restrictions macro to change or differentially weight __bbad before the final addition of the components of design badness takes place.

The %MktEx macro usually produces nearly balanced designs, but if balance is critically important, and your designs are not balanced enough, you can sometimes achieve better balance by specifying the BALANCE= argument. However, this improvement in balance is usually obtained at the cost of less efficiency. Another approach is to instead use the %MktBal macro, which produces designs that are guaranteed to have optimal balance for main-effects designs without restrictions.

When you specify BALANCE= (particularly if you specify BALANCE=0), you should also specify MINTRY=t (perhaps something like MINTRY= $5 * n$ or MINTRY= $10 * n$ , where n is the number of rows in the design). When you specify both BALANCE= and MINTRY=t, the balance restrictions are ignored for the first $t - 3 * n / 2$ passes through the design. During this period, the badness function for the balance restrictions is set to 1 so that the %MktEx macro knows that the design does not conform. After that, all restrictions are considered.

The BALANCE= argument works best when its restrictions are imposed on a reasonably efficient design. You can specify BALANCE=0 without specifying MINTRY=, but this might not be a good idea because the macro needs the flexibility to have imbalance as it refines the design. Often, the design that is actually found has better balance than your BALANCE=d specification requires. Therefore, it is good to start by specifying a value larger than the minimum acceptable value. The larger the value that is specified in the BALANCE= argument, the more freedom the macro has to optimize both balance and efficiency.

EXAMINE= <I> <V> <ALIASING=n <FULL> <MAIN> >

specifies the matrices that you want to examine. EXAMINE=I displays the information matrix $\bX ’\bX$ , EXAMINE=V displays the variance matrix ${(\bX ’\bX )}^{-1}$ , and EXAMINE=I V displays both. These matrices are not displayed by default.

Specify EXAMINE=ALIASING=n to examine the aliasing structure of the design; up to n-factor interactions are displayed. For example, if you specify EXAMINE=ALIASING=2, the %MktEx macro displays the terms in the model and how they are aliased with up to two-factor interactions.

You can also specify FULL (for example, EXAMINE=ALIASING=2 FULL) to see the full aliasing structure that PROC GLM produces directly. You can also specify MAIN to see only the estimable functions that begin with main effects, not the ones that begin with interactions. Interactions are still used with EXAMINE=ALIASING=2 MAIN and larger values of ALIASING=. The MAIN argument just removes some of the output.

Note: The ALIASING=n argument is resource-intensive for larger problems. For some large problems, one of the underlying procedures might detect that the problem is too big, immediately issue an error, and quit. For other large problems, it might simply take a long time to complete or to issue an error message because of insufficient resources. The number of two-way interaction terms is a quadratic function of the number of main effects, so it is not possible to print the aliasing structure even for some reasonably sized main-effects designs.

INTERACT=interaction-list

specifies interactions that must be estimable. By default, no interactions are guaranteed to be estimable.

For example:

interact=x1*x2
interact=x1*x2 x3*x4*x5
interact=x1|x2|x3|x4|x5@2
interact=@2

The interaction syntax is in most ways like that of PROC GLM and many of the other SAS/STAT modeling procedures. It uses "*" for simple interactions (for example, x1*x2 is the interaction between x1 and x2), "|" for main effects and interactions (for example, x1|x2|x3 is the same as x1 x2 x1*x2 x3 x1*x3 x2*x3 x1*x2*x3), and "@" to eliminate higher-order interactions (for example, x1|x2|x3@2 eliminates x1*x2*x3 and is equivalent to x1 x2 x1*x2 x3 x1*x3 x2*x3). The specification "@2" creates main effects and two-way interactions. In contrast with the GLM procedure’s syntax, some shortcuts are permitted. For the factor names, either you can specify the actual variable names (for example, x1*x2 $\ldots$ ) or you can specify the factor number without the "x" (for example, 1*2). You can also specify INTERACT=@2 to indicate all main effects and two-way interactions, omitting the 1|2|.... The following three specifications are equivalent:

%mktex(2 ** 5, interact=@2, n=16)
%mktex(2 ** 5, interact=1|2|3|4|5@2, n=16)
%mktex(2 ** 5, interact=x1|x2|x3|x4|x5@2, n=16)

A resolution V design is requested if you specify INTERACT=@2 and your specification matches a regular fractional-factorial design. However, if you specify the full interaction list (for example, INTERACT=x1 | x2 | x3 | x4 | x5@2), then the less direct approach of requesting a design that has the full list of interaction terms is taken, and in some cases, it might not work as well as directly requesting a resolution V design.

MINTRY=t

specifies the minimum number of rows to process for each design before giving up. You can specify a number or a DATA step expression that involves n (rows) and m (columns). The default number for t is n. For example, to ensure that the macro passes through each row of the design at least five times, you can specify MINTRY=5 * n. This argument can be useful when you have certain restrictions, particularly with the BALANCE= argument. When you specify both BALANCE= and MINTRY=t, the balance restrictions are ignored for the first $t - 3 * n / 2$ passes through the design. During this period, the badness function for the balance restrictions is set to 1, thus informing the %MktEx macro that the design does not conform. After that, all restrictions are considered. The BALANCE= argument works best when its restrictions are imposed on a reasonably efficient design.

The %MktEx macro sometimes displays the following message:

WARNING: It may be impossible to meet all restrictions.

This message is displayed after n rows are passed without any success. Sometimes, it is premature to expect any success during the first pass. When you know this, specifying MINTRY=t, with t $>$ n, prevents the macro from issuing the warning.

OPTIONS=options-list

specifies binary arguments. You can specify one or more of the following values.

ACCEPT

enables the macro to output designs that violate restrictions imposed by the RESTRICTIONS=, BALANCE=, or PARTIAL= argument or have duplicates when OPTIONS=NODUPS. usually, the macro does not output such designs. When OPTIONS=ACCEPT, a design becomes eligible for output when the macro can no longer improve on the restrictions or eliminate duplicates. When you do not specify OPTIONS=ACCEPT, a design is eligible only when all restrictions are met.

CHECK

checks the efficiency of a given design, which you specify in the INIT= argument, and disables the OUT=, OUTR=, and OUTALL= arguments. If you do not specify INIT=, then OPTIONS=CHECK is ignored.

FILE

renders the design to a file that has a computer-generated filename. For example, if the design $2^{11} 3^{12}$ in 36 runs is requested, the generated filename is OA(36,211,312). This argument is ignored unless you also specify OPTIONS=RENDER.

INT

adds an intercept to the design. The intercept variable is named X0.

JUSTINIT

requests that the macro stop processing after the initial design is generated, even if that design would not normally be the final design. The resulting design is usually an orthogonal array or some function of an orthogonal array, but this is not guaranteed. OPTIONS=JUSTINIT implies OPTITER=0 and OUTR=. Specifying OPTIONS=JUSTINIT NOFINAL stops the processing and prevents the final design from being evaluated. When you specify OPTIONS=NOFINAL, you must ensure that the design has a suitable efficiency.

LARGEDESIGN

enables the macro to stop after the number of minutes specified in the MAXTIME= argument has elapsed in the coordinate-exchange algorithm. You usually use this argument together with MAXSTAGES=1 and other arguments that enable the algorithm to run faster. By default, the macro checks the elapsed time when it finishes with a design. Specifying this argument causes the macro to check the elapsed time at the end of each row, after it has completed the first full pass through the design, and after any restrictions have been met; therefore, the macro might stop before D-efficiency has converged. For very large problems and problems that include restrictions, this argument can enable the macro to run faster but at a cost of lower D-efficiency.

LINEAGE

displays the lineage, or "family tree," of the orthogonal array. For example, the lineage of the design $2^1 3^{25}$ in 54 runs is 54**1 : 54**1 > 3**20 6**1 9**1 : 9**1 > 3**4 : 6**1 > 2**1 3**1. This states that the design starts as a single 54-level factor, and then $54^1$ is replaced by $3^{20} 6^1 9^1$ , $9^1$ is replaced by $3^4$ , and $6^1$ is replaced by $2^1 3^1$ to generate the final design.

NODUPS

eliminates duplicate runs.

NOFINAL

omits calling PROC OPTEX to display the efficiency of the final experimental design.

NOHISTORY

suppresses the display of the iteration history.

NOOADUPS

requests that the macro determine whether a design that has duplicate runs is created when performing orthogonal array construction, and if so, that it attempt to avoid duplicates by using other factors from the larger orthogonal array. There is no guarantee that this technique will succeed. If you select a small subset of the columns of an orthogonal array, duplicates might be unavoidable. To ensure no duplicates, even at the expense of nonorthogonality, specify OPTIONS=NODUPS.

NOQC

indicates that you do not have SAS/QC software installed and the %MktEx macro must avoid calling SAS/QC procedures. The macro then attempts to use the coordinate exchange and orthogonal array code, without using PROC FACTEX and PROC OPTEX. This means that the %MktEx macro skips generating a candidate set, searching the candidate set, and displaying the final efficiency values. Specifying this argument is equivalent to specifying OPTITER=0 and OPTIONS=NOFINAL.

OPTIONS=NOQC prevents the macro from checking to see whether the SAS/QC software is available. The SAS/QC procedures are necessary for some problems (for example, some orthogonal arrays in 128 runs) but not for all. For some problems, although the SAS/QC procedures are not necessary, the macro might find better designs if SAS/QC is available (for example, models with interactions and candidate sets on the order of a few thousand observations).

NOSORT

specifies not to sort the design. You might use this argument with orthogonal arrays and Hadamard matrices because some Hadamard matrices are generated using a banded structure that is lost when the design is sorted. Specifying this argument enables you to see the original structure, not just a design.

NOX

suppresses the creation of the internal variables X1, X2, X3, and so on, which by default are available for use in a restrictions macro. If you are not using these variable names in your restrictions macro, this argument enables the macro to run more efficiently.

QUICK

is equivalent to specifying OPTITER=0, MAXDESIGNS=2, UNBALANCED=0, and TABITER=1. This argument provides a quick run that makes at most two designs by using coordinate-exchange iterations. The macro generates the first design by using an initial design that is based on the orthogonal array table (catalog). If necessary, it generates a second design by using random initialization.

QUICKR

is equivalent to specifying OPTITER=0, MAXDESIGNS=1, UNBALANCED=0, and TABITER=0. Specifying OPTIONS=QUICKR provides an even quicker run than specifying OPTIONS=QUICK. It creates only one design by using coordinate exchange and a random initialization. (The "R" in QUICKR stands for random.) You can use this argument when you think that using an initial design from the orthogonal array catalog will not help.

QUICKT

is equivalent to specifying OPTITER=0, MAXDESIGNS=1, UNBALANCED=0, and TABITER=1. This argument provides an even quicker run than OPTIONS=QUICKR. It creates only one design by using coordinate exchange and by using a design from the orthogonal array table (catalog) in the initialization. (The "T" in QUICKT stands for table.)

REFINE

specifies that for an INIT= design data set that has at least one nonpositive entry, each successive design iteration tries to refine the previous best design. By default, the part of the design that is not fixed is randomly reinitialized each time. The default strategy is usually superior.

RENDER

displays the design compactly in the SAS listing. If you specify OPTIONS=RENDER FILE, the design is rendered to a file whose name represents the design specification. For example, if you request the design $2^{11} 3^{12}$ in 36 runs, the generated filename is OA(36,211,312).

RESREP

reports on the progress of the restrictions. You should specify this argument for problems that have nontrivial restrictions. Always specify this argument if the %MktEx macro is unable to create a design that conforms to the restrictions. By default, the iteration history is not displayed while the %MktEx macro attempts to make the design conform to the restrictions.

+-

displays –1 as '–' and 1 as '+' in two-level factors when this argument is specified along with OPTIONS=RENDER. You usually specify this argument when you also specify LEVELS=I for displaying Hadamard matrices.

3

modifies the OPTIONS=+- argument so that it also applies to 3-level factors: –1 as '–', 0 as '0', and 1 as '+'.

512

adds some larger designs in 512 runs with mixes of 16-, 8-, 4-, and 2-level factors to the catalog. This provides added flexibility in 512 runs at a cost of potentially much slower run time. This argument replaces the default $4^{160} 32^1$ parent with $16^{32} 32^1$ and adds more than 60,000 new designs to the catalog. Many of these designs are automatically available when you run PROC FACTEX, so do not use this argument unless you have first tried and failed to find the design without it.

PARTIAL=n

specifies a partial-profile design. The default is an ordinary linear model design. For example, specify PARTIAL=4 if you want only four attributes to vary in each row of the design (except for the first run, in which none vary). The PARTIAL= argument works by adding restrictions to the design (see the RESTRICTIONS= argument) and specifying ORDER=RANDOM and EXCHANGE=2. The badness of each row (how far each row is from conforming to the partial-profile restrictions) is evaluated, and the results are stored in the scalar __pbad. When you specify other restrictions, the value that is stored in __pbad is added to the variable Bad, which is created by your restrictions macro. You can use your restrictions macro to change or differentially weight __pbad before the final addition of the components of design badness takes place. The %MktEx macro’s default behavior in creating partial-profile designs is to use pairwise exchanges when exchanging levels (EXCHANGE=2), so the construction is slow. Therefore, you might consider specifying MAXDESIGNS=1 or other arguments to make the macro run faster. For large problems, you might get faster but less desirable results by specifying ORDER=SEQRAN. Specifying OPTIONS=ACCEPT or BALANCE= along with PARTIAL= is not a good idea.

You can use the following two arguments (RESLIST= and RESMAC=) jointly to set up some constant matrices that the restrictions macro can use for certain complicated restrictions. Because the restrictions macro is called often, anything that you can do only once speeds up the algorithm. You can also use these arguments to access a %MktEx macro matrix in your restrictions macro that you normally could not access. This requires knowledge of the internal workings of the %MktEx macro, so it is not a capability that you usually need.

RESLIST=list: specifies a list of constant matrices. Begin all names with an underscore to ensure that they do not conflict with any names that the %MktEx macro uses. If you specify more than one name, you must separate the names with commas.
RESMAC=macro-name: specifies the name of a macro that creates the matrices that are named in the RESLIST= argument. Begin all names, including all intermediate matrix names, with an underscore to ensure that they do not conflict with any names that the %MktEx macro uses.
RESTRICTIONS=macro-name: specifies the name of a macro that places restrictions on the design. By default, there are no restrictions. For more information about writing an effective restrictions macro, see the section Writing a Restrictions Macro.
SEED=n: specifies the random number seed. By default, SEED=0, and clock time is used to make the random number seed. If you specify a random number seed, results should be reproducible within a SAS release for a particular operating system and for a particular version of the macro. However, because of machine and macro differences, some results might not be exactly reproducible everywhere. For most orthogonal and balanced designs, the results should be reproducible. When computerized searches are done, it is likely that you will not get the same design across different computers, different operating systems, and different SAS and macro releases, although you would expect the efficiency differences to be slight.

Data Set Arguments

The following arguments specify the names of the input and output data sets.

CAT=SAS-data-set

specifies the input design catalog. By default, the %MktEx macro automatically runs the %MktOrth macro to get this catalog. However, many designs can be made in multiple ways, so you can run the %MktOrth macro yourself, select the exact design that you want, and specify the resulting data set in the CAT= argument. You use the %MktOrth macro’s OUTLEV= data set, which by default is called MktDesLev, as the CAT= data set. Be sure to specify OPTIONS=DUPS LINEAGE when you run the %MktOrth macro.

For example, the design $2^{71}$ in 72 runs can be made from either $2^{36} 36^1$ or $2^{68} 4^1$ . The following statements show how to select the $2^{36} 36^1$ parent:

%mktorth(range=n=72, OPTIONS=dups lineage)

proc print data=mktdeslev;
   var lineage;
run;

data lev;
   set mktdeslev(where=(x2 = 71 and index(lineage, '2 ** 36 36 ** 1')));
run;

%mktex(2 ** 71, n=72, CAT=lev, out=b)

INIT=SAS-data-set

specifies the initial experimental design. If all values in the initial design are positive, then a first step evaluates the design, the next step tries to improve it, and subsequent steps try to improve the best design that is found. However, if any values in the initial design are nonpositive (or missing), then a different approach is used. The initial design can have three types of values:

positive integers, which are fixed and constant and do not change throughout the course of the iterations
zero and missing values, which are replaced by random values at the start of each new design search and can change throughout the course of the iterations
negative values, which are replaced by their absolute value at the start of each new design attempt and can change throughout the course of the iterations

When absolute orthogonality and balance are required in a few factors, you can fix those factors in advance. The following statements illustrate how:

* Get first four factors;
%mktex(8 6 2 2, n=48)

* Flag the first four as fixed and set up to solve for the next six;
data init;
   set design;
   retain x5-x10 .;
run;

* Get the last factors, holding the first four fixed;
%mktex(8 6 2 2 4**6,          /* append 4**6 to 8 6 2 2  */
       n=48,                  /* 48 runs                 */
       init=init,             /* initial design          */
       maxiter=100)           /* 100 iterations          */

%mkteval(data=design)

Alternatively, you can use the HOLDOUTS= or FIXED= argument to fix just certain rows.

OUT=SAS-data-set

names the output data set that contains the final experimental design. By default, OUT=Design. By default, this design is sorted unless you specify OPTIONS=NOSORT. You can use this output data to evaluate the design. Specify a null value for the OUT= argument if you do not want the %MktEx macro to create this data set. The OUTR= argument creates a randomized version of the same design, which is usually more suitable for actual use.

OUTALL=SAS-data-set

names the output data set that contains all the designs found. By default, this data set is not created. This data set contains the design number, the efficiency, and the design. When you use this argument, you can break while the macro is running and still recover the best design that has been found so far. However, the designs are saved in this data set only when the macro is finished processing them. For example, design 1 is saved once at the end of processing, not every time an improvement is found along the way.

OUTEFF=SAS-data-set

names the output data set that contains the final efficiencies, the method that is used to find the design, and the initial random number seed. This data set is not created by default.

OUTR=SAS-data-set

names the output data set that contains the randomized version of the final experimental design. By default, the data set is named Randomized. In this version of the design, levels are randomly reassigned within factors and the runs are sorted into random order. Neither of these operations affects efficiency. When you specify the RESTRICTIONS= or PARTIAL= argument, only the random sort is performed. Specify a null value for the OUTR= argument if you do not want a randomized design to be created.

Iteration Arguments

The following group of arguments control some of the details of the %MktEx macro’s iterations. The macro can perform three sets of iterations: the algorithm search, the design search, and the design refinements.

The algorithm search iterations look for efficient designs by using three different approaches. The macro then determines which approach appears to be working best and uses that approach exclusively in the design search iterations. The design refinement iterations try to refine the best design that has been found by using level exchanges together with random mutations and simulated annealing. Some of these iteration arguments accept up to three parameters, one for each set of iterations.

ANNEAL=n1 <n2 <n3>>

specifies the starting probability for simulated annealing in the coordinate-exchange algorithm. By default, ANNEAL=.05 .05 .01. You can specify a zero or null value to request no annealing. You can specify more than one value if you want to use different values for the algorithm search, design search, and design refinement iterations. When you specify a value greater than 0 and less than 1 (for example, 0.1), the design is permitted to get worse with decreasing probability as the number of iterations increases. This often helps the algorithm overcome local efficiency maxima. Permitting efficiency to decrease can help get past local maxima in the efficiency function.

For example, ANNEAL= or ANNEAL=0 specifies no annealing. ANNEAL=0.1 specifies an annealing probability of 0.1 during all three sets of iterations. ANNEAL=0 0.1 0.05 specifies no annealing during the initial iterations, an annealing probability of 0.1 during the search iterations, and an annealing probability of 0.05 during the refinement iterations.

ANNITER=n1 <n2 <n3>>

specifies the first iteration during which the macro is to consider using annealing on the design. By default, ANNITER=. . ., which means that the macro chooses the values to use. The default is the first iteration that uses a fully random initial design in each of the three sets of iterations. By default, no random annealing occurs in any part of the initial design when part of the initial design comes from an orthogonal design.

CANDITER=n1 < n2 >

specifies the number of coordinate-exchange iterations to use during the algorithm search and the design search in order to improve a candidate set-based initial design that is generated by PROC OPTEX. By default, CANDITER=1 1. You should not change these values unless you are using annealing or mutation in the CANDITER= iterations or unless you are specifying OPTIONS=NODUPS.

MAXDESIGNS=n

requests that the macro stop after n designs have been created.

MAXITER=n1 <n2 <n3>> ITER=n1 <n2 <n3>>

specifies the maximum number of iterations or designs to generate. By default, MAXITER=21 25 10. Larger values tend to produce better designs at a cost of slower run times. You can specify more than one value if you want to use different values for the algorithm search, design search, and design refinement iterations. The second value is used only if the second set of iterations consists of coordinate-exchange iterations. Otherwise, the number of iterations for the second set is specified using the TABITER= argument or the CANDITER= and OPTITER= arguments. If you want more iterations, you must also specify the MAXTIME= argument, because the iteration process stops when the maximum number of iterations is reached or the maximum amount of time has elapsed, whichever comes first.

For examples, MAXITER=10 specifies 10 iterations for the initial, search, and refinement iterations. MAXITER=10 10 5 specifies 10 initial iterations, 10 search iterations, and then 5 refinement iterations.

MAXSTAGES=n

requests that the macro stop after n algorithm stages have been completed. This argument is useful for big designs and when the macro runs slowly because of restrictions. If you specify MAXSTAGES=1, the macro stops after the algorithm search stage; if you specify MAXSTAGES=2, the macro stops after the design search stage. By default, MAXSTAGES=3, which means that the macro stops after the design refinement stage.

MAXTIME=n1 <n2 <n3>>

specifies the approximate maximum number of minutes to run each phase. By default, MAXTIME=10 20 5. When an iteration completes (a design is completed), the macro quits iterating in that phase if the elapsed time exceeds the specified number of minutes. The run time is usually no more than 10% or 20% greater than the specified values. However, the macro checks time only after a design finishes, so the run time can be quite a bit longer than the specified value for large problems, problems with restrictions, and problems with EXCHANGE= argument values other than 1.

You can specify more than one value if you want to use different values for the algorithm search, design search, and design refinement iterations. During the algorithm search iterations, if one-half of the first time value has been exceeded and the macro is not finished using orthogonal initializations, and it has passed, the macro switches to using a random initial design. The second value is ignored for PROC OPTEX iterations because PROC OPTEX does not have any timing arguments.

You can specify MAXTIME=0 to get a quick run that performs no more than one iteration in each phase. However, even when MAXTIME=0, run time can be several minutes or more for large problems. For other ways to drastically cut run time for large problems, see the MAXDESIGNS= and MAXSTAGES= arguments. If you specify very large time values (anything more than hours), you should also specify the OPTITER= argument, because its default values depend on the MAXTIME= value.

MUTATE=n1 <n2 <n3>>

specifies the probability at which each value in an initial design can mutate or be assigned a different random value before the coordinate-exchange iterations begin. By default, MUTATE=.05 .05 .01. Specify a zero or null value to request no mutation. You can specify more than one value if you want to use different values for the algorithm search, design search, and design refinement iterations.

MUTITER=n1 <n2 <n3>>

specifies the first iteration during which the macro is to consider mutating the design. By default, MUTITER=. . ., which means that the macro chooses the values to use. The default is the first iteration that uses a fully random initial design in each of the three sets of iterations. By default, no random mutations occur in any part of the initial design when part of the initial design comes from an orthogonal design.

OPTITER=n1 <n2 >

specifies the number of iterations to use in the candidate-set based searches that are performed by PROC OPTEX in the algorithm and design search iterations. By default, OPTITER= $\ldots$ , which means that the macro chooses the values to use. When the first value is "." (missing), the macro chooses a value that is usually no less than 20 for larger problems and usually no greater than 200 for smaller problems. However, MAXTIME= argument values other than the default values can cause the macro to choose values that are outside this range. When the second value is missing, the macro chooses a value that is based on how long the first PROC OPTEX run takes and the value of the MAXTIME= argument, but that is no greater than 5,000. However, when a missing value is specified for the first OPTITER= argument value, the default, the macro can choose not to perform any PROC OPTEX iterations to save time if it determines that it can find a perfect design without them.

REPEAT=n1 n2 n3

specifies the maximum number of times to work on a row to eliminate restriction violations. By default, REPEAT=25 . ., which specifies to work on a row up to 25 times to eliminate violations. The second value is the place in the design refinement where this processing starts. This is based on a zero-based total number of rows processed so far. This is like a zero-based row index, but it never resets within a design. The third value is the place where this extra repeated processing stops. Let m be the MINTRY=m value, which by default is n, the number of rows. By default, when the second value is missing, the process starts after m rows have been processed (the second complete pass through the design). By default, the process stops after $n2 + 10 * n$ rows have been processed, where n2 is the second (specified or derived) REPEAT= value.

TABITER=n1 < n2 >

specifies the number of times to try to improve an orthogonal or fractional-factorial initial design. By default, TABITER=10 200, which specifies 10 iterations in the algorithm search and 200 iterations in the design search.

UNBALANCED=n1 < n2 >

specifies the proportion of the TABITER= argument iterations for which the macro considers using unbalanced factors in the initial design. By default, UNBALANCED=.2 .1. One way that unbalanced factors occur is through coding down. Coding down, for example, creates a 3-level factor from a 4-level factor, $(1 \; 2 \; 3 \; 4) \Rightarrow (1 \; 2 \; 3 \; 3)$ , or a 2-level factor from a 3-level factor, $(1 \; 2 \; 3) \Rightarrow (1 \; 2 \; 2)$ . For any particular problem, this strategy will probably work either really well or not well at all. The UNBALANCED= argument tries to create 2-level through 5-level factors from 3-level through 6-level factors.

Miscellaneous Arguments

The following are miscellaneous arguments that you might occasionally find useful.

BIG=n <CHOOSE>

specifies the size of a full-factorial-design that is considered to be big. By default, BIG=5185 CHOOSE. When the full-factorial design is smaller than the BIG= value, the %MktEx macro searches a full-factorial candidate set. Otherwise, it searches a fractional-factorial candidate set. When CHOOSE (the default) is also specified, the macro can choose to use a fractional-factorial even when the full-factorial design is not too big, if it appears that the final design can be created from the fractional-factorial design.

EXCHANGE=n

specifies the number of factors to consider at a time when levels are exchanged. You can specify EXCHANGE=2 to do pairwise exchanges. Pairwise exchanges are much slower, but they might produce better designs. For this reason, you might want to specify MAXTIME=0 or MAXDESIGNS=1 or other iteration arguments to make fewer designs and make the macro run faster. The EXCHANGE= argument interacts with the ORDER= argument. ORDER=SEQRAN is faster with EXCHANGE=2 than ORDER=SEQUENTIAL or ORDER=RANDOM. By default, EXCHANGE=2 when the PARTIAL= argument is specified. When ORDER=MATRIX, the EXCHANGE= argument value is the number of matrix columns. Otherwise, the default is EXCHANGE=1.

It is important to do pairwise exchanges with partial-profile designs and certain other highly restricted designs. For example, consider the following design row in which PARTIAL=4:

1 1 2 3 1 1 1 2 1 1 1 3

The %MktEx macro cannot consider changing a 1 to a 2 or 3 unless it can also consider changing one of the current 2’s or 3’s to 1 to maintain the partial-profile restriction of exactly four values not equal to 1. Specifying EXCHANGE=2 gives the %MktEx macro that flexibility.

FIXED=variable

specifies an INIT= data set variable that indicates which runs are fixed (cannot be changed) and which ones can be changed. By default, no runs are fixed.

The values of the specified variable are interpreted as follows:

1 (or any nonmissing value) means that this run must never change.
0 means that this run is used in the initial design, but it can be swapped out.
. means that this run should be randomly initialized, and it can be swapped out.

You can use this argument to add holdout runs to a conjoint design (but see the HOLDOUTS= argument for an easier way). To fix parts of the design in a much more general way, see the INIT= argument.

HOLDOUTS=n

adds holdout observations to the INIT= data set. This argument augments an initial design. Specifying HOLDOUTS=n optimally adds n runs to the INIT= design. HOLDOUTS=n works by adding a FIXED= argument variable and extra runs to the INIT= data set. Do not specify both the FIXED= and HOLDOUTS= arguments. The number of rows in the INIT= design plus the value that you specify in the HOLDOUTS= argument must equal the N= argument value.

LEVELS=values

specifies the method of assigning the final factor levels. This recoding occurs after the design is created, so all restrictions must be expressed in terms of one-based factors, regardless of what is specified in the LEVELS= argument.

The valid values and their interpetations are as follows:

1 – default, one-based, the levels are 1, 2, $\ldots$
0 – zero-based, the levels are 0, 1, $\ldots$
c – centered, possibly resulting in nonintegers, 1 2 $\rightarrow$ –0.5 0.5, 1 2 3 $\rightarrow$ –1 0 1
i – centered and scaled to integers, 1 2 $\rightarrow$ –1 1, 1 2 3 $\rightarrow$ –1 0 1

You can also specify separate values for 2- and 3-level factors by preceding a value with "2" or "3". For example, LEVELS=2 i 3 0 c means 2-level factors are coded –1, 1 and 3-level factors are coded 0, 1, 2. The remaining factors are centered. The centering is based on centering the level values, not on centering the (potentially unbalanced) factor. For example, the centered levels for a 2-level factor in five runs (1 2 1 2 1) are (–0.5 0.5 –0.5 0.5 –0.5), not (–0.4 0.6 –0.4 0.6 –0.4). If you want the latter form of centering, specify M=0 in PROC STANDARD. For more general level setting, see the %MktLab macro.

You can also specify the following three values:

FIRST – requests that the first row of the design consist entirely of the first level
LAST – requests that the first row of the design consist entirely of the last level, which is useful for Hadamard matrices
INT – adds an intercept column to the design

specifies the order in which the columns are processed by the coordinate exchange algorithm. You can specify the following values:

: COL=n processes n random columns in each row.
: MATRIX=SAS-data-set reads the order from a data set.
: RANDOM specifies random order.
: RANDOM=n specifies random order with partial-profile exchanges.
: RANSEQ specifies sequential order from a random first column.
: SEQRAN is an alias for RANSEQ.
: SEQUENTIAL specifies 1, 2, 3, $\ldots$

By default, ORDER=RANDOM when there are partial-profile restrictions, ORDER=RANSEQ when there are other restrictions, and ORDER=SEQUENTIAL otherwise.

For ORDER=COL=n, specify an integer for n, such as ORDER=COL=2. You should use this specification only for very large problems where you do not care whether you hit every column. This argument is usually used in conjunction with OPTIONS=LARGEDESIGN QUICKR. You can use it when you have a large problem and you do not have enough time for one complete pass through the design, when you just want to iterate for approximately the MAXTIME= amount of time and then stop. You should not use ORDER=COL= with restrictions.

ORDER=RANDOM=n is similar to ORDER=RANDOM, but with an adaptation that is particularly useful for partial-profile choice designs. Use this specification with EXCHANGE=2. For example, suppose you are making a partial-profile design that has 10 attributes and three alternatives. Attribute 1 is made from X1, X11, and X21; attribute 2 is made from X2, X12, and X22; and so on. Specifying ORDER=RANDOM=10 means that the columns, as shown by column index J1, are traversed in random order. A second loop (indexed by variable J2) traverses all the factors in the current attribute. For example, when J1 is 13, J2 = 3, 13, 23. This performs pairwise exchanges within choice attributes.

The ORDER= argument interacts with the EXCHANGE= argument. With random order and EXCHANGE=2, the variable J1 loops over the columns of the design in random order, and for each J1, J2 loops over the columns greater than J1 in random order. With a sequential order and EXCHANGE=2, the variable J1 loops over the columns in 1, 2, 3 order, and for each J1, J2 loops over the columns greater than J1 in a J1+1, J1+2, J1+3 order. ORDER=RANSEQ is different. When EXCHANGE=2, the variable J1 loops over the columns in an order $r$ , $r+1$ , $r+2$ , $\ldots$ , m, 1, 2, $\ldots$ , $r-1$ (for random $r$ ), and for each J1 there is a single random J2. Hence, ORDER=RANSEQ is the fastest specification, because it considers just one pair rather than all pairs. ORDER=RANSEQ provides the only situation where you might try EXCHANGE=3.

ORDER=MATRIX=SAS-data-set enables you to specify exactly which columns are worked on, in what order, and in what groups. The SAS data set provides one row for every column grouping. For example, suppose you want to use this argument to work on columns in pairs. (You could just use EXCHANGE=2). The data set will have two variables. The first variable contains the number of a design column, and the second variable contains the number of a second column that is to be exchanged with the first. The names of the variables are arbitrary. The following steps create and display an example data set for five factors:

%let m = 5;
data ex;
   do i = 1 to &m;
      do j = i + 1 to &m;
         output;
      end;
   end;
run;

proc print noobs;
run;

The results are shown in Figure 1.

Figure 1: ORDER=MATRIX Data Set

i	j
1	2
1	3
1	4
1	5
2	3
2	4
2	5
3	4
3	5
4	5

The specified EXCHANGE= argument value is ignored, and the actual EXCHANGE= value is set to 2 because the data set has two columns. The values must be integers between 1 and m, where m is the number of factors. The values can also be missing, except in the first column. Missing values are replaced by a random column (potentially a different random column each time).

In a model that contains interactions, you can use this argument to ensure that the terms that enter into interactions together are processed together. This is illustrated in the following statements:

data mat;
  input x1-x3;
  datalines;
1 1 1
2 3 .
2 4 .
3 4 .
2 3 4
5 5 .
6 7 .
8 . .
;

%mktex(4 4 2 2 3 3 2 3, n=36, order=matrix=mat,
       interact=x2*x3 x2*x4 x3*x4 x6*x7,  seed=472)

The data set Mat contains eight rows, so eight column groupings are processed. The data set contains three columns, so up to 3-way exchanges are considered. The first row mentions column 1 three times. Any repeats of a column number are ignored, so the first group of columns simply consists of column 1. The second column consists of 2, 3, and ., so the second group consists of columns 2, 3, and some random column. The random column could be any of the columns that include 2 and 3, so sometimes this will be a 2-way exchange and sometimes a 3-way exchange. This group is specified because x2*x3 is one of the interaction terms. Similarly, other groups consist of the other 2-way interaction terms and a random factor: 2 and 4, 3 and 4, and 6 and 7. In addition, there is one 3-way term to help with the three 2-way interactions that involve x2, x3, and x4. Each time, the exchange algorithm considers $4 \times 2 \times 2$ exchanges, the product of the three numbers of levels. In principle, there is no limit on the number of columns, but in practice, this number can easily get too big to be useful for more than a few exchanges at a time. The row 5 5 . requests an exchange between column 5 and a random factor. The row 8 . . requests an exchange between column 8 and two random factors.

STOPEARLY=n

specifies that the macro can stop early when it finds the same maximum D-efficiency repeatedly in different designs. By default, STOPEARLY=5. By default, during the design search iterations and refinement iterations, the macro stops early if it finds a D-efficiency equal to but not greater than the maximum 5 times. This might mean that the macro has found the optimal design, or it might mean that the macro keeps finding a very attractive local optimum. Either way, it is unlikely to improve. When the macro stops for this reason, the macro displays the following message:

NOTE: Stopping since it appears that no improvement is possible.

You can specify either 0 or a very large value to turn off the stop-early checking.

TABSIZE=n

provides you with some control over which design (orthogonal array, PROC FACTEX, or Hadamard) from the orthogonal array table (catalog) is to be used for the partial initialization when an exact match is not found. Specify the number of runs in the orthogonal array. By default, the macro chooses an orthogonal design that best matches the specified design. For more detailed control, see the CAT= argument.

TARGET=n

specifies the target efficiency criterion. By default, TARGET=100. The macro stops when it finds an efficiency value greater than or equal to this number. If you know what the maximum efficiency criterion is, or if you know how big is big enough, you can enable the macro to run faster by letting it stop when it reaches the specified efficiency. You can also use this argument if you just want to see the initial design that the %MktEx macro is using: TARGET=1, OPTITER=0. If you specify TARGET=1, the macro stops after the initialization, provided that the initial efficiency is greater than 1.

Esoteric Arguments

The following are all the other miscellaneous arguments. You will rarely specify arguments from this list.

ANNEALFUN=function: specifies the function that controls how the simulated annealing probability changes with each pass through the design. By default, ANNEALFUN=ANNEAL * 0.85. Note: The IML operator # performs ordinary (scalar) multiplication. Most users will never need this argument.
DETFUZZ=n: specifies the value to use to evaluate whether determinants are changing. By default, DETFUZZ=1e-8. If NEWDETER > OLDDETER * (1 + DETFUZZ), then the new determinant is larger. If NEWDETER > OLDDETER * (1 - DETFUZZ), then the new determinant is the same. Otherwise, the new determinant is smaller. Most users will never need this argument.
IMLOPTS=options: specifies PROC IML statement options. For example, for very large problems, you can use this argument to specify the IML SYMSIZE= or WORKSIZE= option: IMLOPTS=SYMSIZE=n WORKSIZE=m, substituting numeric values for n and m. The defaults for these PROC IML options are host-dependent. Most users will never need this argument.
RIDGE=n: specifies a value to add to the diagonal of $\bX ’\bX$ to make it nonsingular. By default, RIDGE=1e-7. For normal problems, you usually do not need to change this value. If you want the macro to create designs that have more parameters than runs, you must specify some other value (usually something like 0.01). By default, the macro quits when there are more parameters than runs. Specifying a RIDGE= argument value other than the default (even if you just change the "e" in 1e–7 to "E") enables the macro to create a design that has more parameters than runs. You sometimes need this argument for advanced design problems.

Help Argument

You can specify either of the following to display the argument names and simple examples of the macro syntax:

%mktex(help)
%mktex(?)

%MktEx Macro Notes

The %MktEx macro displays notes in the SAS log to show you what it is doing while it is running. Most of the notes that would usually come out of the macro’s procedure and DATA steps are suppressed by default by an options nonotes statement. This macro specifies options nonotes throughout most of its execution. If you want to see all the notes, submit the statement %let mktopts = notes; before running the macro. To see the macro version, submit the statement %let mktopts = version; before running the macro. This section describes the notes that are usually not suppressed.

The macro usually starts by displaying one of the following notes (filling in a value after N=):

NOTE: Generating the Hadamard design, n=.
NOTE: Generating the full-factorial design, n=.
NOTE: Generating the fractional-factorial design, n=.
NOTE: Generating the orthogonal array design, n=.

These messages tell you which type of orthogonal design the macro is constructing. The design might be the final design, or it might provide an initialization for the coordinate exchange algorithm. In some cases, it might not have the same number of runs, n, as the final design. This step is usually fast, but constructing some fractional-factorial designs can be time-consuming.

The macro displays the following note when it is going to use PROC OPTEX to search a candidate set:

NOTE: Generating the candidate set.

This step is usually fast. Next, when a candidate set is searched, the macro displays the following note, substituting values for the ellipses:

NOTE: Performing ... searches of ... candidates.

This step can take some time, depending on the size of the candidate set and the size of the design. When there are a lot of restrictions and a fractional-factorial candidate set is being used, the candidate set might be so restricted that it does not contain enough information to make the design. In that case, you will get the following message:

NOTE: The candidate-set initialization failed,
      but the MKTEX macro is continuing.

Even though part of the macro’s algorithm failed, it is not a problem. The macro just goes on to the coordinate-exchange algorithm, which will almost certainly work better than searching any severely restricted candidate set.

For large designs, you will usually want to skip the PROC OPTEX iterations. The macro might display the following note:

NOTE: With a design this large, you may get faster results with OPTITER=0.

Sometimes you will get the following note:

NOTE: Stopping since it appears that no improvement is possible.

When the macro repeatedly finds the same maximum D-efficiency in different designs, it might stop early. This might mean that the macro has found the optimal design, or it might mean that the macro keeps finding a very attractive local optimum. Either way, it is unlikely to improve. You can control this action by using the STOPEARLY= argument.

The macro has arguments that control the amount of time that it spends trying different techniques. When time expires, the macro might switch to other techniques before it completes the usual maximum number of iterations. When this happens, the macro displays the following notes:

NOTE: Switching to a random initialization after ... minutes and
   ... designs.
NOTE: Quitting the algorithm search after ... minutes and ... designs.
NOTE: Quitting the design search after ... minutes and ... designs.
NOTE: Quitting the refinement step after ... minutes and ... designs.

When there are restrictions, or when you specify that you do not want duplicate runs, you can also specify OPTIONS=ACCEPT. This means that you are willing to accept designs that violate the restrictions. When you specify OPTIONS=ACCEPT, the macro displays the following notes to tell you if the restrictions are not met:

NOTE: The restrictions were not met.
NOTE: The design has duplicate runs.

The %MktEx macro optimizes a ridged efficiency criterion; that is, a small number is added to the diagonal of ${(\bX ’\bX )}^{-1}$ . Usually, the ridged criterion is virtually the same as the unridged criterion. When the %MktEx macro detects that this is not true, it displays the following notes:

NOTE: The final  ridged D-efficiency criterion is ....
NOTE: The final unridged D-efficiency criterion is ....

The macro ends with one of the following two messages:

NOTE: The MKTEX macro used ... seconds.
NOTE: The MKTEX macro used ... minutes.

Writing a Restrictions Macro

To impose restrictions on the design, you write a macro that creates a variable called Bad that contains a numerical summary of how bad the row of the design is. When everything is fine, you set Bad to 0. Otherwise, you set Bad to a larger value that is a function of the number of restriction violations. The Bad variable must not be binary (0 – OK, 1 – bad) unless there is only one simple restriction. You must set Bad so that the %MktEx macro knows whether the changes that it is considering are moving the design in the right direction. The macro must consist of PROC IML statements and possibly some SAS macro language statements.

When you have restrictions, you can specify OPTIONS=RESREP to get a report on the restriction violations in the iteration history. This can be a great help when you debug your restrictions macro. Also, be sure to check the log when you specify the RESTRICTIONS= argument. The %MktEx macro cannot always ensure that your statements are free of syntax errors and stop if they are not. There are a number of macro arguments that you can use to impose restrictions, including RESTRICTIONS=, OPTIONS=NODUPS, BALANCE=, PARTIAL=, and INIT=. If you specify more than one of these arguments, be sure that the combination makes sense and that it is possible to simultaneously satisfy all the restrictions.

The %MktEx macro makes a number of scalars, a row vector, and a matrix available that you can use in your restictions macro to quantify badness. You refer to these quantities in your restrictions macro by using the following names:

I – a scalar that contains the number of the row that is currently being changed or evaluated. If you are writing restrictions that use the variable I, you should almost certainly specify OPTIONS=NOSORT.
Try – a scalar similar to I, which contains the number of the row that is currently being changed. However, Try starts at 0 and is incremented for each row; it is set back to 0 when a new design starts, not when the %MktEx macro reaches the last row. Use I as a matrix index and Try to evaluate how far the %MktEx macro is into the process of constructing the design.
X – a row vector of factor levels for row I that always contains integer values that begin with 1 and continue on to the number of levels for each factor. These values are always one-based, even if the LEVELS= argument is specified.
X1 – the same as X[1]; X2 is the same as X[2]; and so on.
J1 – a scalar that contains the number of the column that is currently being changed. In the steps where the restrictions macro is called once per row, J1 = 1.
J2 – a scalar that contains the number of the other column that is currently being changed (along with J1) when EXCHANGE=2. Both J1 and J2 are defined when the EXCHANGE= argument value is greater than or equal to 2. This scalar does not exist when EXCHANGE=1. In the steps where the restrictions macro is called once per row, J1 = J21 = 1.
J3 – a scalar that contains the number of the third column that is currently being changed (along with J1 and J2) when the EXCHANGE= argument value is greater than or equal to 3. This scalar does not exist when EXCHANGE=1 and EXCHANGE=2. There will be a J4, J5, and so on, if and only if the EXCHANGE= argument value is greater than 3. In the steps where the restrictions macro is called once per row, J1 = J2 = J3 = 1.
Xmat – the entire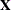 $\bX$ matrix. The ith row of 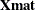$\mb{Xmat}$ is often different from 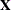$\bX$ because 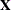$\bX$ contains information about the exchanges being considered, whereas 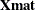$\mb{Xmat}$ contains the current design.
Bad – the variable that contains the number of violations of restrictions. You can make the value of this variable large or small, and you can use integers or real numbers. However, the values should always be nonnegative. When there are multiple sources of design badness, it is good to put the different sources on different scales so that they do not trade off against each other. For example, for the first source, you might multiply the number of violations by 1,000, by 100 for another source, by 10 for another source, by 1 for another source, and even sometimes by 0.1 or 0.01 for other sources. The final badness is the sum of Bad, __pbad (when it exists), and __bbad (when it exists).
__pbad – the badness from the PARTIAL= argument. This scalar does not exist when the PARTIAL= argument is not specified. You can weight this value in your restrictions macro (usually by multiplying it by a constant) to differentially weight the contributors to badness; for example: __pbad = __pbad * 10.
__bbad – the badness from the BALANCE= argument. This scalar does not exist when the BALANCE= argument is not specified. You can weight this value in your restrictions macro (usually by multiplying it by a constant) to differentially weight the contributors to badness; for example: __bbad = __bbad * 100.

You cannot use these names (other than Bad) for intermediate values! Otherwise, you can create intermediate variables without worrying about conflicts with the names in the macro. The levels of the factors for one row of the experimental design are stored in a vector X; the first level is always 1, the second level is always 2, and so on. All restrictions must be defined in terms of X[j] (or alternatively, X1, X2, $\ldots$ , and perhaps the other matrices). For example, suppose there are five 3-level factors. If you want to define badness to mean that the level of a factor equals the level of the following factor, you can write the following macro, named RESTRICT, and specify RESTRICTIONS=RESTRICT when you invoke the %MktEx macro:

%macro restrict;
   bad = (x1 = x2) +
   (x2 = x3) +
   (x3 = x4) +
   (x4 = x5);
%mend;

When you specify the RESTRICTIONS= argument, you specify just the macro name with no percent sign.

When you write a restrictions macro, there are a few facts about PROC IML that you should keep in mind. PROC IML does not have the same full set of Boolean operators that the DATA step and other parts of SAS have. For example, the following operators are not available in PROC IML: OR, AND, NOT, GT, LT, GE, LE, EQ, and NE. Also, although the expression a <= b <= c is perfectly valid in PROC IML, its meaning is different from and less reasonable than its meaning in a DATA step. The DATA step expression checks to see whether b is in the range of a to c. In contrast, the PROC IML expression a <= b <= c is exactly the same as (a <= b) <= c, which evaluates (a <= b) and sets the result to 0 (false) or 1 (true). PROC IML then compares the resulting 0 or 1 to see whether it is less than or equal to c.

The operators that you can use, along with their meanings, are as follows:

		Do Not
Specify	For	Specify
$=$	Equal	EQ
$\wedge =$ or $\neg =$	Not equal	NE
$<$	Less than	LT
$<=$	Less than or equal to	LE
$>$	Greater than	GT
$>=$	Greater than or equal to	GE
$\&$	And	AND
$\|$	Or	OR
$\wedge$ or $\neg$	Not	NOT
`a <= b` & `b <= c`	Range check	`a <= b <= c`

When you impose restrictions, the Current D-Efficiency column of the iteration history table can contain values that are larger than those in the Best D-Efficiency column. This is because the design that corresponds to the current D-efficiency might have restriction violations. Values are reported in the best D-efficiency column only after all the restriction violations have been removed. You can specify OPTIONS=ACCEPT together with the RESTRICTIONS= argument when it is acceptable if the restrictions are not met.

Advanced Restrictions

It is extremely important when imposing restrictions that you appropriately quantify the badness of the run. When the %MktEx macro considers an exchange, it has to know whether it is doing one of the following:

eliminating restriction violations, thus making the design better
causing more restriction violations, thus making the design worse
making a change that neither increases nor decreases the number of violations

Your restrictions macro must inform the %MktEx macro when it is making progress in the right direction. If it does not provide this information, the %MktEx macro will probably not find an acceptable design.

Complicated Restrictions

Consider designing a choice experiment with two alternatives, each composed of 25 attributes, the first 22 of which have restrictions on them. Attribute 1 in the choice design is made from X1 and X23, attribute 2 in the choice design is made from X2 and X24, and so on. The attributes greater than 22 are made from X45 – X50. Each of the 25 choice-design attributes is made from the following pairs of factors:

…

x10

…

x21

x22

x45

x46

x47

x23

x24

x25

x26

x27

x28

x29

x30

x31

x32

…

x43

x44

x48

x49

x50

The restrictions are as follows: each choice attribute must contain two 1’s between five and nine times, each choice attribute must contain one 1 between five and nine times, and each choice attribute must contain two 2’s between five and nine times. When there are multicomponent restrictions such as these, it is easy to make mistakes when you are writing the restrictions macro. Even when your macro correctly differentiates rows that conform to the restrictions and rows that do not conform, the restrictions macro might not give the %MktEx macro enough guidance. Common mistakes include not quantifying the degree of badness in a row of the design. This section illustrates this and other problems that you might encounter when writing restrictions macros, and then shows one possible solution.

The following steps show an example of how not to program the restrictions:

%macro sumres;
   allone = 0; oneone = 0; alltwo = 0;
   do k = 1 to 22;
      if      (x[k] = 1 & x[k+22] = 1) then allone = allone + 1;
      else if (x[k] = 1 & x[k+22] = 2) |
              (x[k] = 2 & x[k+22] = 1) then oneone = oneone + 1;
      else if (x[k] = 2 & x[k+22] = 2) then alltwo = alltwo + 1;
   end;

* Bad example.  Need to quantify badness.;
bad = (^((5 <= allone & allone <= 9) &
         (5 <= oneone & oneone <= 9) &
         (5 <= alltwo & alltwo <= 9)));
%mend;

%mktex(3 ** 50,                     /* 50 three-level factors               */
       n=135,                       /* 135 runs                             */
       restrictions=sumres,         /* name of restrictions macro           */
       seed=289,                    /* random number seed                   */
       options=resrep               /* restrictions report                  */
               quickr               /* very quick run with random init      */
               nox)                 /* suppresses x1, x2, x3 ... creation   */

The macro begins by initializing three counts to 0. The scalar Allone is the count of the number of choice-design attributes that are all 1’s, Onelone is the count of the number of choice-design attributes that have one 1 and one 2, and Alltwo is the count of the number of choice-design attributes that have two 2’s. The DO loop runs through the 22 attributes and increments each of the three counts every time one of the desired patterns is found. Everything in and above the DO loop is fine. The problem occurs next. The assignment statement after the DO loop creates the scalar Bad and sets it to 1 when the counts are not in the required range and 0 otherwise. This assignment statement stores the results of a Boolean expression. When the scalars Allone, Onelone, and Alltwo are all in the right range, each of the inner expressions is true (1), as is the result of the three expressions and the two AND operations. The caret (NOT operator) converts true to false and false to true so that the scalar bad is set to 0 when nothing bad happened and 1 when something bad happened.

In the %MktEx macro, you specify OPTIONS=RESREP to produce a report in the iteration history on the process of meeting the restrictions. When you run the %MktEx macro and it is having trouble making a design that conforms to restrictions, this report can be extremely helpful. Some of the results of this step are as follows:

                            Algorithm Search History

                                   Current          Best
           Design    Row,Col  D-Efficiency  D-Efficiency  Notes
           ----------------------------------------------------------
                1      Start       59.7632                Ran,Mut,Ann
                1      1           60.4198                1 Violations
                1      2           61.0591                1 Violations
                1      3           61.6890                1 Violations
                1      4           62.4063                1 Violations
                1      5           62.8670                1 Violations
                1      6           63.6578                1 Violations
                1      7           64.1437                1 Violations
                1      8           64.4543                1 Violations
                1      9           64.8995                1 Violations
                1     10           65.6750                1 Violations
                .
                .
                .
                .
                1    131           86.4159                1 Violations
                1    132           86.4921                1 Violations
                1    133           86.4709                1 Violations
                1    134           86.5461                1 Violations
                1    135           86.5328                1 Violations
                1      1           86.5825                1 Violations
WARNING: It might be impossible to meet all restrictions.
                .
                .
                .
                1    133           89.4985                0 Violations
                .
                .
                .

The macro succeeds in eliminating restriction violations only in occasional rows. The problem with the preceding approach is that there are complicated restrictions but badness is binary. If all the counts are in the right range, badness is 0; otherwise it is 1. You need to write a macro that lets the %MktEx macro know when it is going in the right direction or it will probably never find a suitable design. You need to let it know, in an attribute with a 2 and a 1, that if it turns a 2 into a 1, it has taken a step toward increasing the Allone count and toward decreasing the Oneone count, and then appropriately update the badness criterion. This does not happen when badness is binary.

One thing that is correct about the preceding code is the compound Boolean range expressions like (5 <= allone & allone <= 9). Abbreviated expressions like (5 <= allone <= 9) that work correctly in the DATA step work incorrectly and without warning in PROC IML. Another thing that is correct is the way the %SumRes macro creates new variables, K, Allone, Oneone, and Alltwo. Care was taken to avoid using names like I and X that conflict with the matrices that you can examine in quantifying badness. The full list of names that you must avoid are I, Try, X, X1, X2 through Xn for n factors, J1, J2, J3, and Xmat. The following steps show a slightly better but still misguided example of the macro:

%macro sumres;
   allone = 0; oneone = 0; alltwo = 0;
   do k = 1 to 22;
      if      (x[k] = 1 & x[k+22] = 1) then allone = allone + 1;
      else if (x[k] = 1 & x[k+22] = 2) |
              (x[k] = 2 & x[k+22] = 1) then oneone = oneone + 1;
      else if (x[k] = 2 & x[k+22] = 2) then alltwo = alltwo + 1;
   end;

   * Better, badness is quantified, and almost correctly too!;
   bad = (^((5 <= allone & allone <= 9) &
            (5 <= oneone & oneone <= 9) &
            (5 <= alltwo & alltwo <= 9))) #
         (abs(allone - 7) + abs(oneone - 7) + abs(alltwo - 7));
%mend;

%mktex(3 ** 50,                     /* 50 three-level factors               */
       n=135,                       /* 135 runs                             */
       restrictions=sumres,         /* name of restrictions macro           */
       seed=289,                    /* random number seed                   */
       options=resrep               /* restrictions report                  */
               quickr               /* very quick run with random init      */
               nox)                 /* suppresses x1, x2, x3 ... creation   */

At first glance, this restrictions macro seems to do everything right—it quantifies badness—but a closer examination is warranted. The variables Allone, Oneone, and Alltwo count the number of times that choice attributes are all one, have exactly one 1, or are all 2, respectively. Everything is fine when the all-one count is in the range 5 to 9: (5 <= allone & allone <= 9); and the exactly-one-1 count is in the range 5 to 9: (5 <= oneone & oneone <= 9); and the all-two count is in the range 5 to 9: (5 <= alltwo & alltwo <= 9). It is bad when this is not true: (((5 <= allone & allone <= 9) & (5 <= oneone & oneone <= 9) & (5 <= alltwo & alltwo <= 9))); the Boolean NOT operator "" performs the logical negation. This Boolean expression is 1 for bad and 0 for OK. It is multiplied by a sum of how far these counts are outside the correct range: (abs(allone - 7) + abs(oneone - 7) + abs(alltwo - 7)). When the row meets all the restrictions, this sum of absolute differences is multiplied by 0. Otherwise badness gets larger as the counts get further away from the middle of the 5-to-9 interval.

Some of the output from running the preceding macros follows:

                            Algorithm Search History

                                   Current          Best
           Design    Row,Col  D-Efficiency  D-Efficiency  Notes
           ----------------------------------------------------------
                1      Start       59.7632                Ran,Mut,Ann
                1      1           60.3423                6 Violations
                1      2           60.7620                0 Violations
                1      3           61.1314                4 Violations
                1      4           61.6805                5 Violations
                1      5           62.1363                0 Violations
                1      6           62.5948                0 Violations
                1      7           62.9039                4 Violations
                1      8           63.1492                0 Violations
                1      9           63.4927                4 Violations
                1     10           63.8624                0 Violations
                1     11           64.3188                5 Violations
                .
                .
                .
                .
                1     12           64.7603                5 Violations
                1    133           64.7106                3 Violations
                1    134           64.3932                5 Violations
                1    135           64.2997                0 Violations

These results are from the first pass through the design. When OPTIONS=RESREP, the %MktEx macro displays one line per row along with the number of violations when it is finished with the row. The macro is succeeding in eliminating violations in some but not all rows. This is the first thing that you should look for. If the macro is not succeeding in any rows, you might have written a set of restrictions that is impossible to satisfy. Some of the output from the second pass through the design is as follows:

                1      1           64.3119                0 Violations
                1      2           64.3272                0 Violations
                1      3           64.4162                0 Violations
                1      4           64.6035                0 Violations
                1      5           64.6395                0 Violations
                1      6           64.7770                0 Violations
                1      7           64.9521                0 Violations
                .
                .
                .
                1     28           66.8037                4 Violations
                1     28           66.6859                0 Violations
                .
                .
                .
                1     69           68.7250                5 Violations
                1     69           68.6878                5 Violations
                1     69           68.7250                5 Violations
                1     69           68.6789                5 Violations
                1     69           68.7250                5 Violations
                .
                .
                .
                1     69           68.7114                5 Violations
                1     69           68.7114                5 Violations
                .
                .
                .
                1    133           71.9063                0 Violations
                1    134           71.9149                0 Violations
                1    135           71.9333                0 Violations

In the second pass, the %MktEx macro tries extra hard to impose restrictions in situations where it had some reasonable success in the first pass. You can see that it is trying over and over again without success to impose the restrictions in the 69th row. You can also see that it has no trouble removing all violations in the 28th row that were still there after the first pass. The %MktEx macro produces volumes of output like this. For several iterations, it will devote extra attention to rows that have some violations, but in this case without complete success. When you see this pattern—some success but also some stubborn rows that the %MktEx macro cannot fix—there might be something wrong with your restrictions macro. Are you really telling the %MktEx macro when it is doing a better job? The preceding steps illustrate some of the things that can go wrong with restrictions macros. It is important to carefully evaluate the results—look at the design, look at the iteration history, specify OPTIONS=RESREP, and so on—to ensure that your restrictions are doing what you want. In this example, the problem is the quantification of badness in the following statement:

bad = (^((5 <= allone & allone <= 9) &
         (5 <= oneone & oneone <= 9) &
         (5 <= alltwo & alltwo <= 9))) #
      (abs(allone - 7) + abs(oneone - 7) + abs(alltwo - 7));

There are three nonindependent contributors to the badness function: the three counts (Allone, Oneone, and Alltwo). As a factor level changes, one count can increase while another decreases. There is a larger problem too. Suppose that Allone and Oneone are in the correct range but Alltwo is not. Then the function fragments abs(Allone - 7) and abs(Oneone - 7) incorrectly contribute to the badness function. The solution is to clearly differentiate the three sources of badness and to weight the pieces so that one part never trades off against the others. For example, consider the following modified restrictions macro:

%macro sumres;
   allone = 0; oneone = 0; alltwo = 0;
   do k = 1 to 22;
      if      (x[k] = 1 & x[k+22] = 1) then allone = allone + 1;
      else if (x[k] = 1 & x[k+22] = 2) |
              (x[k] = 2 & x[k+22] = 1) then oneone = oneone + 1;
      else if (x[k] = 2 & x[k+22] = 2) then alltwo = alltwo + 1;
   end;

   bad = 100 # (^(5 <= allone & allone <= 9)) # abs(allone - 7) +
          10 # (^(5 <= oneone & oneone <= 9)) # abs(oneone - 7) +
               (^(5 <= alltwo & alltwo <= 9)) # abs(alltwo - 7);
%mend;

%mktex(3 ** 50,                     /* 50 three-level factors               */
       n=135,                       /* 135 runs                             */
       restrictions=sumres,         /* name of restrictions macro           */
       seed=289,                    /* random number seed                   */
       options=resrep               /* restrictions report                  */
               quickr               /* very quick run with random init      */
               nox)                 /* suppresses x1, x2, x3 ... creation   */

In this version of the restrictions macro, a component of badness contributes to the function only when it is really part of the problem. The first part has a weight of 100, and the second part has a weight of 10. Now the restrictions macro will never change Oneone or Alltwo if that causes a problem for Allone, and it will never change Alltwo if that causes a problem for Oneone. Previously, the %MktEx macro was getting stuck in some rows because it could never figure out how to fix one component of badness without making another component worse. For some problems, figuring out how to differentially weight the components of badness so that they never trade off against each other is the key to writing a successful restrictions macro. It often does not matter which component gets the most weight. What is important is that each component gets a different weight so that the %MktEx macro does not get caught cycling back and forth, making A better and B worse and then making B better and A worse. The following is some of the output from the first pass through the design while using the modified restrictions macro:

                            Algorithm Search History

                                   Current          Best
           Design    Row,Col  D-Efficiency  D-Efficiency  Notes
           ----------------------------------------------------------
                1      Start       59.7632                Ran,Mut,Ann
                1      1           60.2334                4 Violations
                1      2           60.7867                3 Violations
                1      3           61.1763                0 Violations
                1      4           61.4382                0 Violations
                1      5           61.6494                0 Violations
                1      6           62.2171                0 Violations
                1      7           62.1774                0 Violations
                1      8           62.6273                0 Violations
                1      9           63.1095                3 Violations
                1     10           63.4078                0 Violations
                .
                .
                .
                1    131           67.4221                0 Violations
                1    132           66.9651                6 Violations
                1    133           66.7982                0 Violations
                1    134           66.4926                0 Violations
                1    135           66.4555                0 Violations

In the first pass, the %MktEx macro is imposing all restrictions for most, but not all, of the rows. Some of the output from the second pass through the design is as follows:

                1      1           66.5957                3 Violations
                1      1           66.5711                0 Violations
                1      2           66.6860                0 Violations
                1      3           66.7663                0 Violations
                1      4           66.8973                0 Violations
                1      5           67.0152                0 Violations
                1      6           67.0788                0 Violations
                1      7           67.2155                0 Violations
                1      8           67.2721                0 Violations
                1      9           67.4274                0 Violations
                1     10           67.5745                0 Violations
                .
                .
                .
                1     65           71.3709                3 Violations
                1     65           71.3636                3 Violations
                1     65           71.3709                3 Violations
                1     65           71.3709                3 Violations
                1     65           71.3236                0 Violations
                .
                .
                .
                1    131           72.9631                0 Violations
                1    132           72.8559                4 Violations
                1    132           72.8463                3 Violations
                1    132           72.7370                0 Violations
                1    133           72.7681                0 Violations
                1    134           72.7280                0 Violations
                1    135           72.7453                0 Violations

In the second pass, the %MktEx macro imposes all the restrictions in all rows that still had violations after the first pass. The third pass ends with the following output:

                1    130           74.6889                0 Violations
                1    131           74.7175                0 Violations
                1    132           74.7384                0 Violations
                1    133   1       74.7384       74.7384  Conforms
                1    133  44       74.7571       74.7571

The %MktEx macro completes a full pass through row 132, the place of the last violation. It does not find any new violations, so in row 133 it states that the design conforms to the restrictions, and the iteration history proceeds in the normal fashion from then on. The note Conforms is displayed at the place where the %MktEx macro decides that the design conforms. The design continues to conform throughout more iterations, even though the note Conforms is not displayed on every line. The final efficiency of the design is as follows:

                                                                   Average
                                                                  Prediction
    Design                                                         Standard
    Number     D-Efficiency     A-Efficiency     G-Efficiency       Error
    ------------------------------------------------------------------------
         1        80.2237          61.0557          93.7160          0.8650

The following statements create the choice design and display a subset of the design:

%mktkey(x1-x50)

data key;
   input (x1-x25) ($);
   datalines;
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13
x14 x15 x16 x17 x18 x19 x20 x21 x22                  x45 x46 x47
x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34
x35 x36 x37 x38 x39 x40 x41 x42 x43 x44              x48 x49 x50
;

%mktroll(design=design, key=key, out=chdes)

proc print data=chdes;
   by set;
   id set;
   where set le 2 or set ge 134;
run;

Notice the slightly unusual arrangement of the Key data set: the first 22 attributes are made from the first 44 factors of the linear arrangement, and the last 3 attributes are made from the last 6 factors of the linear arrangement.

A sample of four choice sets is shown in Figure 2.

Figure 2: First Two and Last Two Choice Sets

Set	_Alt_	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	x15	x16	x17	x18	x19	x20	x21	x22	x23	x24	x25
1	1	1	1	1	1	1	3	1	2	2	2	3	2	2	1	3	1	1	2	2	1	2	3	3	3	1
1	2	3	2	1	2	3	1	2	2	1	2	1	2	1	1	1	1	1	2	3	1	2	1	1	1	3

Set	_Alt_	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	x15	x16	x17	x18	x19	x20	x21	x22	x23	x24	x25
2	1	1	1	1	1	2	1	1	3	1	2	1	2	2	1	3	3	2	2	2	3	2	3	3	1	2
2	2	1	1	1	1	3	2	2	2	2	3	1	2	2	2	2	2	1	2	2	2	2	2	1	3	1

Set	_Alt_	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	x15	x16	x17	x18	x19	x20	x21	x22	x23	x24	x25
134	1	3	3	3	1	2	1	2	2	1	2	2	1	1	2	1	2	3	1	1	2	1	3	1	2	1
134	2	3	2	2	1	2	3	2	2	1	2	2	1	1	1	2	3	2	2	1	1	2	1	2	1	2

Set	_Alt_	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	x15	x16	x17	x18	x19	x20	x21	x22	x23	x24	x25
135	1	3	3	3	2	2	1	3	2	1	2	1	1	1	3	1	2	1	2	2	2	1	2	3	3	1
135	2	2	1	3	2	2	2	2	3	1	2	1	1	1	2	2	2	1	1	1	2	2	3	1	3	1

Where the Restrictions Macro Gets Called

The restrictions macro is defined and called in four distinct places by the %MktEx macro. First, the %MktEx macro calls the restrictions macro in a preliminary PROC IML step to check for errors in the syntax. Next, it is called in between calling PROC PLAN or PROC FACTEX and calling PROC OPTEX. Here, the restrictions macro is used to impose restrictions on the candidate set. Next, the restrictions macro is used during design creation and by the coordinate-exchange algorithm. Finally, when you specify OPTIONS=ACCEPT, which means that restriction violations are acceptable, the restrictions macro is called after all the iterations have completed and after the %MktEx macro reports any restrictions violations in the final design. For some advanced restrictions, you might not want exactly the same code to run in all four places. When the restrictions are written purely in terms of restrictions on X, which is the ith row of the design matrix, there is no problem. The same restrictions macro works fine for all uses. However, when $\mb{Xmat}$ (the full $\mb{X}$ matrix), I, or J1 (the row or column number) is used, the same code often cannot be used for all applications. The following are notes for each of the four phases.

Syntax Check

In this phase, the macro is defined and called just to check for syntax errors. This step enables the %MktEx macro to end more gracefully when there are errors and to provide you with better information about the nature of the error than it would otherwise. Your restrictions macro can detect when it is in this phase, because the macro variable &main is set to 0 and the macro variable &pass is set to null. The &pass variable is null before the iterations begin, 1 for the algorithm search phase, 2 for the design search phase, 3 for the design refinement stage, and 4 after the iterations end. You can conditionally execute code in this step by using the following macro statements:

%if      &main eq 0 and &pass eq  %then %do;  /* execute in syntax check     */
%if not (&main eq 0 and &pass eq) %then %do;  /* not execute in syntax check */

You usually do not need to worry about this step. The %MktEx macro just calls the restrictions macro once and ignores the results to check for syntax errors. For this step, $\mb{Xmat}$ is a matrix of ones, $\mb{X}$ is a vector of ones (because the design does not exist yet), and J1 = J2 = J3 = I = 1. If you have complicated restrictions that involve the row or column exchange indices (I, J1, J2, or J3), you might need to worry about this step. You might need to either not execute your restrictions in this step or conditionally execute some assignment statements (just for this step) that set up J1, J2, and J3 more appropriately. Sometimes you can set things up appropriately by using the RESMAC= argument. However, be aware that this step checks I, Try, J1, J2, J3, $\mb{X}$ , and $\mb{Xmat}$ after your restrictions macro is called to ensure that you are not changing them; this is usually a sign of an error. If you get the following warning, make sure you are not incorrectly changing one of the matrices that you should not change:

WARNING: Restrictions macro is changing i, try, j1, j2, j3, x, or xmat.
         This might be a serious problem.  Check your macro.

If the %MktEx macro detects a syntax error during this step, it will try to tell you where it is and what the problem is. If you have syntax errors in your restrictions macro and you cannot figure out what they are, sometimes the best option is to directly submit the statements in your restrictions macro to PROC IML to see the syntax errors. But first you need to submit the following statements:

%let n = 27; /* substitute number of runs    */
%let m = 10; /* substitute number of factors */
proc iml;
   xmat = j(&n, &m, 1);
   i = 1;
   j1 = 1;
   j2 = 1;
   j3 = 1;
   bad = 0;
   x = xmat[i,];

Candidate Check

In this phase, the restrictions macro is used to impose restrictions on the candidate set that is created by PROC PLAN or PROC FACTEX, but before it is searched by PROC OPTEX. The restrictions macro is called once for each row for which the column index J1 is set to 1. For some problems, such as most partial-profile problems, the restrictions are so severe that virtually none of the candidates can conform. Also, restrictions that are based on row number and column number do not make sense in the context of a candidate design. Your restrictions macro can detect when it is in this phase because the macro variable &main is set to 0 and the macro variable &pass is set to 1 or 2. You can conditionally execute code in this step by using the following macro statements:

%if      &main eq 0 and &pass ge 1 and &pass le 2
         %then %do;                             /* execute on candidates     */
%if not (&main eq 0 and &pass ge 1 and &pass le 2)
         %then %do;                             /* not execute on candidates */

For simple restrictions that do not involve the column exchange indices (J1, J2, J3), you probably do not need to worry about this step. If you use J1, J2, or J3, you need to either not execute your restrictions in this step or conditionally execute some assignment statements that set up J1, J2, and J3 appropriately. Usually for this step, $\mb{Xmat}$ contains the candidate design, $\mb{X}$ contains the ith row, J1 = 0, J2 = 0, J3 = 0, Try = 1, and I is set to the candidate row number.

Main Coordinate-Exchange Algorithm

In this phase, the restrictions macro is used to impose restrictions on the design as it is being built by the coordinate-exchange algorithm. Your restrictions macro can detect when it is in this phase because the macro variable &main is set to 1 and the macro variable &pass is set to 1, 2, or 3. You can conditionally execute code in this step by using the following macro statements:

%if      &main eq 1 and &pass ge 1 and &pass le 3
         %then %do;                    /* execute on coordinate exchange     */
%if not (&main eq 1 and &pass ge 1 and &pass le 3)
         %then %do;                    /* not execute on coordinate exchange */

For this step, $\mb{Xmat}$ contains the candidate design; $\mb{X}$ contains the ith row; J1, J2, and J3 usually contain the column indices; I is the row number; and Try is the zero-based cumulative row number. When you specify EXCHANGE=1, J1 exists; when you specify EXCHANGE=2, J1 and J2 exist; and so on. Sometimes in this phase, the restrictions macro is called once per row, with the J* indices all set to 1. If you use the J* indices in your restrictions, you might need to allow for this. For example, if you are checking the current J1 column for balance, and you used an INIT= data set with column one fixed and unbalanced, you do not want to perform the check when J1 = 1. For some designs that are partially initialized with an orthogonal array and for some uses of INIT=, not all columns or cells in the design are evaluated.

Restrictions Violations Check

In this phase, the restrictions macro is used to check the design when there are restrictions and OPTIONS=ACCEPT. The restrictions macro is called once for each row of the design. Your restrictions macro can detect when it is in this phase because the macro variable &main is set to 1 and the macro variable &pass is greater than 3. You can conditionally execute code in this step by using the following macro statements:

%if      &main eq 1 and &pass gt 3  %then %do; /* execute on final check     */
%if not (&main eq 1 and &pass gt 3) %then %do; /* not execute on final check */

For this step, $\mb{Xmat}$ contains the candidate design, $\mb{X}$ contains the ith row; J1 = 1, J2 = 1, J3 = 1, Try = 1, and I is the row number.

Example 1: Orthogonal and Balanced Factors—the Linear Arrangement Approach

This example shows how to use the %MktEx macro to find a linear arrangement of a choice design. You can use this approach when you want all the attributes of all the alternatives to be balanced and orthogonal or at least nearly so.

The product is breakfast bars, and there are three brands: Branolicious, Brantopia, and Brantasia. The choice sets consist of the three brands and a constant (no purchase) alternative. Each brand has two attributes: a 4-level attribute for price and a 2-level attribute for the number of bars per box. The prices are $2.89, $2.99, $3.09, and $3.19, and the sizes are six-count and eight-count. You can make a choice design by starting with a design that is optimal for a hypothetical linear model that has factors for all the attributes of all the alternatives. The linear arrangement consists of the six factors, which the following tables show organized by brand and by attribute.

Factors Organized by Brand
Linear			Choice
Factor			Design
Name	Levels	Brand	Attribute
x1	4 levels	Branolicious	Price
x2	2 levels	Branolicious	Count
x3	4 levels	Brantopia	Price
x4	2 levels	Brantopia	Count
x5	4 levels	Brantasia	Price
x6	2 levels	Brantasia	Count

Factors Organized by Attribute
Linear			Choice
Factor			Design
Name	Levels	Brand	Attribute
x1	4 levels	Branolicious	Price
x3	4 levels	Brantopia	Price
x5	4 levels	Brantasia	Price
x2	2 levels	Branolicious	Count
x4	2 levels	Brantopia	Count
x6	2 levels	Brantasia	Count

You need a factorial design that has six factors: Branolicious Price, Branolicious Count, Brantopia Price, Brantopia Count, Brantasia Price, and Brantasia Count. From this design, you make a choice design that has three attributes: brand, count, and price. You can use the %MktRuns macro as follows to suggest the number of choice sets:

%mktruns(4 2  4 2  4 2)

The input to the %MktRuns macro is the number of levels of all the factors (that is, all the attributes of all the alternatives). Figure 3 shows the output of the %MktRuns macro.

Figure 3: %MktRuns Output

                                Design Summary

                            Number of
                            Levels       Frequency

                                 2           3
                                 4           3

               Saturated      = 13
               Full Factorial = 512

               Some Reasonable                      Cannot Be
                  Design Sizes       Violations     Divided By

                            16 *              0
                            32 *              0
                            24                3     16
                            20               12      8 16
                            28               12      8 16
                            14               18      4  8 16
                            18               18      4  8 16
                            22               18      4  8 16
                            26               18      4  8 16
                            30               18      4  8 16
                            13 S             21      2  4  8 16

          * - 100% Efficient design can be made with the MktEx macro.
          S - Saturated Design - The smallest design that can be made.
              Note that the saturated design is not one of the
              recommended designs for this problem.  It is shown
              to provide some context for the recommended sizes.

n	Design	Reference
16	2 6 4 3	Fractional-Factorial
16	2 3 4 4	Fractional-Factorial
32	2 22 4 3	Fractional-Factorial
32	2 19 4 4	Fractional-Factorial
32	2 16 4 5	Fractional-Factorial
32	2 15 4 3 8 ** 1	Fractional-Factorial
32	2 13 4 6	Fractional-Factorial
32	2 12 4 4 8 ** 1	Fractional-Factorial
32	2 10 4 7	Fractional-Factorial
32	2 9 4 5 8 ** 1	Fractional-Factorial
32	2 7 4 8	Fractional-Factorial
32	2 6 4 6 8 ** 1	Fractional-Factorial
32	2 4 4 9	Fractional-Factorial
32	2 3 4 7 8 ** 1	Fractional-Factorial

There are three 2-level factors and three 4-level factors. The saturated design has 13 runs or rows, so you need at least 13 choice sets for this approach. The full-factorial design has 512 runs, so there are a maximum of 512 possible choice sets. The %MktRuns macro suggests 16 as its first choice, because 16 meets the necessary but not sufficient conditions for the existence of an orthogonal array. The number 16 can be divided by 2 (you have 2-level factors), 4 (you have 4-level factors), $2 \times 2$ (you have more than one 2-level factor), $4 \times 4$ (you have more than one 4-level factor), and $2 \times 4$ (you have both 2-level factors and 4-level factors). The number of choice sets must be divisible by all of these if the design is going to be orthogonal and balanced. The number 32 also meets these conditions. However, 16 is a more reasonable number of judgments for people to make, and all the other suggestions (24, 20, 28, 14, 18, 22, 26, 30) cannot be divided by at least one of the relevant numbers. For this example, the macro considers only sizes up to 32. By default, the %MktRuns macro stops considering larger sizes when it finds a perfect size (in this case 32) that is twice as big as another perfect size (16). Sixteen choice sets are ideal for this example. The necessary conditions are sufficient in this case, and there is an orthogonal array that you can use. The last part of the output lists the orthogonal arrays that the %MktEx macro knows how to make that also work for this specification.

The following statement invokes the %MktEx macro to find the factorial design:

%mktex(4 2  4 2  4 2, n=16, seed=17)

The %MktEx macro accepts a factor-level list like the %MktRuns macro list along with the number of runs or choice sets. You can specify a random number seed so that you always get the same design if you rerun the %MktEx macro.

Figure 4 shows the results.

Figure 4: %MktEx Output

Algorithm Search History

                                   Current          Best
           Design    Row,Col  D-Efficiency  D-Efficiency  Notes
           ----------------------------------------------------------
                1      Start      100.0000      100.0000  Tab
                1        End      100.0000

                              The OPTEX Procedure

                            Class Level Information

                             Class  Levels  Values

                             x1       4     1 2 3 4
                             x2       2     1 2
                             x3       4     1 2 3 4
                             x4       2     1 2
                             x5       4     1 2 3 4
                             x6       2     1 2

Design Number	D-Efficiency	A-Efficiency	G-Efficiency	Average Prediction Standard Error
1	100.0000	100.0000	100.0000	0.9014

The %MktEx macro found a 100% efficient, orthogonal, balanced design that has three 2-level factors and three 4-level factors. The levels are all positive integers, starting with 1 and continuing up to the number of levels.

The following statements display the design shown in Figure 5 by using PROC PRINT.

proc print data=Design;
run;

Figure 5: %MktEx Output

Obs	x1	x2	x3	x4	x5	x6
1	1	1	1	1	1	1
2	1	1	3	2	4	2
3	1	2	2	1	3	2
4	1	2	4	2	2	1
5	2	1	2	1	2	1
6	2	1	4	2	3	2
7	2	2	1	1	4	2
8	2	2	3	2	1	1
9	3	1	1	2	2	2
10	3	1	3	1	3	1
11	3	2	2	2	4	1
12	3	2	4	1	1	2
13	4	1	2	2	1	2
14	4	1	4	1	4	1
15	4	2	1	2	3	1
16	4	2	3	1	2	2

Example 2: The Linear Arrangement Approach with Restrictions

This example creates a design for the same study as in the previous example but restricts the design to avoid choice sets where attributes are constant. That is, you want to select just the choice sets where neither price nor count is constant within a choice set.

Restrictions are written by using PROC IML statements that are embedded in a macro. You then provide the name of the restrictions macro to the %MktEx macro by using the RESTRICTIONS= argument. In the restrictions macro, you compute an IML scalar called Bad that quantifies the badness of the design. The %MktEx macro automatically initializes the scalar Bad to 0. In this case, because the restrictions are entirely within each choice set, you can just quantify the badness of one choice set at a time by evaluating the values in the scalars X1–X6, which correspond to the six attributes. If it is easier to use indexing to write the restrictions, you can use the vector $\mb{x}$ , where $\mb{x[1]}$ = x1, $\ldots$ , $\mb{x6}$ = x6 instead. In the restrictions macro %Res that follows, Bad is set to 1 if the Price variable (which is made from x1, x3, and x5) is constant. The scalar Bad is incremented by 1 if the Count variable (which is made from x2, x4, and x6) is constant.

%macro res;
   if x1 = x3 & x1 = x5 then bad = 1;
   if x2 = x4 & x2 = x6 then bad = bad + 1;
%mend;

You now use the %MktEx macro as follows to get a restricted factorial design for this problem:

%mktex(4 2  4 2  4 2, n=16, restrictions=res, seed=17)

Figure 6, Figure 7, Figure 8, and Figure 9 show the %MktEx macro’s output.

Figure 6: %MktEx Algorithm Search History

                                   Current          Best
           Design    Row,Col  D-Efficiency  D-Efficiency  Notes
           ----------------------------------------------------------
                1      Start       91.5504                Can
                1      2   1       91.5504       91.5504  Conforms
                1        End       91.5504

                2      Start      100.0000                Tab
                2     14   1       87.8163                Conforms
                2        End       89.5326

                3      Start      100.0000                Tab
                3     14   1       85.2744                Conforms
                3        End       86.9271

                4      Start      100.0000                Tab
                4     14   1       84.9718                Conforms
                4        End       85.6568

                5      Start      100.0000                Tab
                5     14   1       84.7284                Conforms
                5        End       87.3099

                6      Start      100.0000                Tab
                6     14   1       85.5377                Conforms
                6        End       86.9731

                7      Start      100.0000                Tab
                7     14   1       82.8801                Conforms
                7        End       88.0734

                8      Start      100.0000                Tab
                8     14   1       84.0164                Conforms
                8        End       89.2343

                9      Start      100.0000                Tab
                9     14   1       82.9864                Conforms
                9        End       87.2147

               10      Start      100.0000                Tab
               10     14   1       86.8052                Conforms
               10        End       87.5513

               11      Start      100.0000                Tab
               11     14   1       85.0061                Conforms
               11        End       88.7427

               12      Start       61.3114                Ran,Mut,Ann
               12     16   1       79.4843                Conforms
               12        End       89.1152

               13      Start       59.3474                Ran,Mut,Ann
               13      9   1       88.1603                Conforms
               13        End       90.8211

               14      Start        5.9399                Ran,Mut,Ann
               14     16   1       77.8656                Conforms
               14        End       91.5287

               15      Start       59.5266                Ran,Mut,Ann
               15     13   1       85.6026                Conforms
               15        End       87.1962

               16      Start       60.1559                Ran,Mut,Ann
               16     11   1       83.9377                Conforms
               16        End       88.2425

               17      Start       67.1759                Ran,Mut,Ann
               17     15   1       85.3701                Conforms
               17        End       90.6546

               18      Start       62.9917                Ran,Mut,Ann
               18      1   1       81.9340                Conforms
               18        End       89.6519

               19      Start       59.6925                Ran,Mut,Ann
               19     15   1       85.4777                Conforms
               19        End       90.9198

               20      Start       60.8733                Ran,Mut,Ann
               20     16   1       81.5568                Conforms
               20        End       89.9440

               21      Start       53.6255                Ran,Mut,Ann
               21     16   1       81.3052                Conforms
               21        End       89.5758

Figure 7: %MktEx Design Search History

                                   Current          Best
           Design    Row,Col  D-Efficiency  D-Efficiency  Notes
           ----------------------------------------------------------
                0    Initial       91.5504       91.5504  Ini

                1      Start       91.5504                Can
                1      2   1       91.5504       91.5504  Conforms
                1        End       91.5504

Figure 8: %MktEx Design Refinement History

                                   Current          Best
           Design    Row,Col  D-Efficiency  D-Efficiency  Notes
           ----------------------------------------------------------
                0    Initial       91.5504       91.5504  Ini

                1      Start       85.9351                Pre,Mut,Ann
                1      2   1       89.2144                Conforms
                1     11   1       91.5504       91.5504
                1     15   3       91.5504       91.5504
                1     11   5       91.5504       91.5504
                1     16   1       91.5504       91.5504
                1      2   1       91.5504       91.5504
                1        End       91.5504

                2      Start       88.9014                Pre,Mut,Ann
                2      2   1       85.7076                Conforms
                2        End       90.7905

                3      Start       89.2953                Pre,Mut,Ann
                3      2   1       88.6625                Conforms
                3        End       89.7394

                4      Start       91.5504                Pre,Mut,Ann
                4      2   1       91.5504       91.5504  Conforms
                4        End       90.8114

                5      Start       87.5177                Pre,Mut,Ann
                5     13   1       83.8041                Conforms
                5        End       88.9568

                6      Start       88.5059                Pre,Mut,Ann
                6      2   1       91.5504       91.5504  Conforms
                6      7   3       91.5504       91.5504
                6        End       91.5504

                7      Start       91.5504                Pre,Mut,Ann
                7      2   1       90.0520                Conforms
                7     11   1       91.5504       91.5504
                7        End       91.5287

                8      Start       92.1768                Pre,Mut,Ann
                8      7   1       88.0433                Conforms
                8        End       88.8908

                9      Start       91.5504                Pre,Mut,Ann
                9      2   1       91.5504       91.5504  Conforms
                9        End       87.4793

Figure 9: %MktEx Output

                              The OPTEX Procedure

                            Class Level Information

                             Class  Levels  Values

                             x1       4     1 2 3 4
                             x2       2     1 2
                             x3       4     1 2 3 4
                             x4       2     1 2
                             x5       4     1 2 3 4
                             x6       2     1 2

Design Number	D-Efficiency	A-Efficiency	G-Efficiency	Average Prediction Standard Error
1	91.5504	80.7068	93.8194	0.9014

The %MktEx macro succeeds in making the design conform to all restrictions. In all cases, it reports zero violations of the restrictions. In some cases, a design that has 100% D-efficiency is replaced by a design that has a lower D-efficiency as the restrictions are imposed. The final D-efficiency is 91.5504. Designs that have this same D-efficiency are repeatedly found, often indicating that the final design is an optimal design.

The following statements display the design shown in Figure 10 by using PROC PRINT.

proc print data=Design;
run;

Figure 10: %MktEx Output

Obs	x1	x2	x3	x4	x5	x6
1	1	1	2	2	4	1
2	1	1	3	2	3	2
3	1	2	1	1	2	2
4	1	2	4	1	1	1
5	2	1	1	2	1	1
6	2	1	4	1	4	2
7	2	2	2	2	3	1
8	2	2	3	1	4	2
9	3	1	1	1	3	2
10	3	1	4	2	2	2
11	3	2	2	1	1	2
12	3	2	3	1	2	1
13	4	1	2	1	2	2
14	4	1	3	2	1	2
15	4	2	1	2	4	1
16	4	2	4	1	3	1

Obs	x1	x2	x3	x4	x5	x6
1	1	1	1	1	1	1
2	1	1	3	2	4	2
3	1	2	2	1	3	2
4	1	2	4	2	2	1
5	2	1	2	1	2	1
6	2	1	4	2	3	2
7	2	2	1	1	4	2
8	2	2	3	2	1	1
9	3	1	1	2	2	2
10	3	1	3	1	3	1
11	3	2	2	2	4	1
12	3	2	4	1	1	2
13	4	1	2	2	1	2
14	4	1	4	1	4	1
15	4	2	1	2	3	1
16	4	2	3	1	2	2

Obs	x1	x2	x3	x4	x5	x6
1	1	1	2	2	4	1
2	1	1	3	2	3	2
3	1	2	1	1	2	2
4	1	2	4	1	1	1
5	2	1	1	2	1	1
6	2	1	4	1	4	2
7	2	2	2	2	3	1
8	2	2	3	1	4	2
9	3	1	1	1	3	2
10	3	1	4	2	2	2
11	3	2	2	1	1	2
12	3	2	3	1	2	1
13	4	1	2	1	2	2
14	4	1	3	2	1	2
15	4	2	1	2	4	1
16	4	2	4	1	3	1

Obs	x1	x2	x3	x4	x5	x6
1	1	1	1	1	1	1
2	1	1	3	2	4	2
3	1	2	2	1	3	2
4	1	2	4	2	2	1
5	2	1	2	1	2	1
6	2	1	4	2	3	2
7	2	2	1	1	4	2
8	2	2	3	2	1	1
9	3	1	1	2	2	2
10	3	1	3	1	3	1
11	3	2	2	2	4	1
12	3	2	4	1	1	2
13	4	1	2	2	1	2
14	4	1	4	1	4	1
15	4	2	1	2	3	1
16	4	2	3	1	2	2

Obs	x1	x2	x3	x4	x5	x6
1	1	1	2	2	4	1
2	1	1	3	2	3	2
3	1	2	1	1	2	2
4	1	2	4	1	1	1
5	2	1	1	2	1	1
6	2	1	4	1	4	2
7	2	2	2	2	3	1
8	2	2	3	1	4	2
9	3	1	1	1	3	2
10	3	1	4	2	2	2
11	3	2	2	1	1	2
12	3	2	3	1	2	1
13	4	1	2	1	2	2
14	4	1	3	2	1	2
15	4	2	1	2	4	1
16	4	2	4	1	3	1

FOCUS AREAS