The %MktDes Macro

specifies the factors and the number of levels for each factor. The following simple example creates a design that has ten 2-level factors:

%mktdes(factors=x1-x10=2)

First, a factor list, which is a valid SAS variable list, is specified. The factor list must be followed by an equal sign and an integer, which gives the number of levels. Multiple lists can be specified. For example, to create five 2-level factors, five 3-level factors, and five 5-level factors, specify

%mktdes(factors=x1-x5=2 x6-x10=3 x11-x15=5)

By default, this macro creates each factor in a fractional-factorial candidate set from a minimum number of pseudo-factors. Pseudo-factors are not output; they are used to create the factors of interest and then discarded. For example, when NLEV=2, a three-level factor X1 is created from two 2-level pseudo-factors (_1 and _2) and their interaction by coding down:

(_1=1, _2=1) -> x1=1
(_1=1, _2=2) -> x1=2
(_1=2, _2=1) -> x1=3
(_1=2, _2=2) -> x1=1

This creates imbalance—the 1 level appears twice as often as the 2 and 3 levels. You can obtain somewhat better balance by instead using three pseudo-factors. You can specify the number of pseudo-factors in parentheses after the number of levels, for example, as follows:

%mktdes(factors=x1-x5=2 x6-x10=3(3))

The levels 1 to 8 are coded down to 1 2 3 1 2 3 1 3, which is better balanced. The cost is that candidate-set size might increase and efficiency might actually decrease. Some researchers are willing to sacrifice a little bit of efficiency in order to achieve better balance.

specifies the size at which the candidate set is considered to be big. By default, BIG=2188. If the size of the full-factorial design is less than or equal to this size, and if PROC PLAN is in the RUN= argument list, the macro uses PROC PLAN instead of PROC FACTEX to create the candidate set. The default of 2,188 is 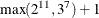. Specifying values as large as BIG=6000 or even slightly larger is often reasonable. However, run time is slower as the size of the candidate set increases. The %MktEx macro coordinate-exchange algorithm usually works better than a candidate-set search when the full-factorial design has more than several thousand runs.

specifies the output data set that contains the candidate design (from PROC FACTEX or PROC PLAN). The default name is Cand, followed by the step number—for example, Cand1 for step 1, Cand2 for step 2, and so on. You should use this option only when you are reading an external candidate set. When you specify STEP= argument values greater than 1, the macro assumes that the default candidate set names, Cand1, Cand2, and so on, were used in previous steps. Specify only a data set name and no data set options.

specifies CLASS statement options in PROC OPTEX. By default, CLASSOPTS=PARAM=ORTHREF. You should probably never change this option.

specifies the CODING= option in PROC OPTEX.

specifies the matrices that you want to examine. EXAMINE=I displays the information matrix, 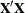; EXAMINE=V displays the variance matrix, 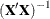; and EXAMINE=I V displays both. These matrices are not displayed by default.

specifies statement options in PROC FACTEX.

specifies the GENERATE statement options in PROC OPTEX. By default, additional options are not added to the GENERATE statement.

specifies interactions that must be estimable. By default, no interactions are guaranteed to be estimable. Examples include the following:

interact=x1*x2
interact=x1*x2 x3*x4*x5
interact=x1|x2|x3|x4|x5@2
interact=@2}

The interaction syntax is similar to that of PROC GLM and many other SAS/STAT procedures. It uses "*" for simple interactions (x1*x2 is the interaction between x1 and x2), "|" for main effects and interactions (x1|x2|x3 is the same as x1 x2 x1*x2 x3 x1*x3 x2*x3 x1*x2*x3), and "@" to eliminate higher-order interactions (x1|x2|x3@2 eliminates x1*x2*x3 and is the same as x1 x2 x1*x2 x3 x1*x3 x2*x3). The specification "@2" creates main effects and two-way interactions. Only "@" values of 2 or 3 are permitted. If you specify "@2" by itself, a resolution V design is requested when PROC FACTEX is run.

specifies the ITER= option in PROC OPTEX, which creates n designs. By default, ITER=10.

specifies the KEEP= option in PROC OPTEX, which keeps the n best designs. By default, KEEP=5.

specifies the number of levels from which factors are constructed through pseudo-factors and coding down. The value must be a prime or a power of a prime: 2, 3, 4, 5, 7, 8, 9, 11, and so on. This argument is used with PROC FACTEX as follows:

factors factors / nlev=&nlev;

By default, the macro uses the minimum prime or power of a prime from the FACTORS= argument list, or 2 if no suitable value is found.

specifies the METHOD= search method option in PROC OPTEX. By default, METHOD=M_FEDOROV (modified Fedorov).

specifies the N= option in PROC OPTEX, which is the number of runs in the final design. The default is the PROC OPTEX default and depends on the problem. You usually do not want to use the default. Instead, you should pick a value by using as guidance the information produced by the %MktRuns macro. N=SATURATED creates a design that has the minimum number of runs.

specifies binary options. You can specify one or more of the following values:

By default, none of these binary options are specified.

specifies other terms to mention in the FACTORS statement in PROC FACTEX. These terms are not guaranteed to be estimable. By default, there are no other factors.

specifies interaction terms that will be specified using PROC OPTEX only for multistep macro invocations. By default, no interactions are guaranteed to be estimable. Normally, interactions that are specified via the INTERACT= option affect the MODEL statements in both PROC FACTEX and PROC OPTEX. In multistep problems, part of an interaction might not be in a particular PROC FACTEX step. In that case, the interaction term must appear only in the PROC OPTEX step. For example, if X1 is created in one step and X4 is created in another, and if the X1*X4 interaction must be estimable, specify OTHERINT=X1*X4 in the final step, which runs PROC OPTEX. The following steps create the design:

%mktdes(step=1, factors=x1-x3=2, n=30, run=factex)

%mktdes(step=2, factors=x4-x6=3, n=30, run=factex)

%mktdes(step=3, factors=x7-x9=5, n=30, run=factex optex,
        otherint=x1*x4)

specifies the output experimental design (from PROC OPTEX). By default, OUT=Design.

specifies PROC OPTEX statement options. By default, no options are added to the PROC OPTEX statement.

specifies the list of procedures that the macro can run. Usually, the macro runs either PROC FACTEX or PROC PLAN and then PROC OPTEX. By default, RUN=PLAN FACTEX OPTEX. You can skip steps by omitting procedure names from this list. When both PROC PLAN and PROC FACTEX are in the list, the macro chooses between them based on the size of the full-factorial design and the value of the BIG= argument. When PROC PLAN is not in the list, the macro generates code for PROC FACTEX.

specifies the random number seed. By default, SEED=0, and clock time is used to make the random number seed.

specifies the size of the candidate set. This argument is used together with PROC FACTEX as follows:

size design=&size;

By default, SIZE=MIN.

specifies the step number. By default, there is only one step. However, sometimes, a better design can be found by using a multistep approach. Do not specify the CAND= argument in any step of a multistep run. Consider the problem of making a design that has three 2-level factors, three 3-level factors, and three 5-level factors. The simplest approach is to do something like creating a design from 2-level factors by using pseudo-factors and coding down:

%mktdes(factors=x1-x3=2 x4-x6=3 x7-x9=5, n=30)

However, for small problems like this, the following three-step approach is usually better:

%mktdes(step=1, factors=x1-x3=2, n=30, run=factex)
%mktdes(step=2, factors=x4-x6=3, n=30, run=factex)
%mktdes(step=3, factors=x7-x9=5, n=30, run=factex optex)

Note, however, that the following %MktEx macro step is usually better still:

%mktex(2 2 2 3 3 3 5 5 5, n=30)

The first %MktDes macro step uses PROC FACTEX to create a fractional-factorial design for the 2-level factors. The second step uses PROC FACTEX to create a fractional-factorial design for the 3-level factors and cross it with the 2-level factors. The third step uses PROC FACTEX to create a fractional-factorial design for the 5-level factors and cross it with the design for the 2- and 3-level factors and then run PROC OPTEX.

Each step globally stores two macro variables (&class1 and &inter1 for the first step, &class2 and &inter2 for the second step, and so on) that are used to construct the CLASS and MODEL statements in PROC OPTEX. When the value of the STEP= argument is greater than 1, variables from the previous steps are used in the CLASS and MODEL statements. In this example, the following PROC OPTEX code is created by the third step:

proc optex data=Cand3;
   class x1-x3 x4-x6 x7-x9 / param=orthref;
   model x1-x3 x4-x6 x7-x9;
   generate n=30 iter=10 keep=5 method=m_fedorov;
   output out=Design;
   run; quit;

This step uses the previously stored macro variables &class1=x1-x3 and &class2=x4-x6.

specifies a SAS WHERE clause for the candidate design, which is used to restrict the candidates. By default, the candidate design is not restricted.