The VARIOGRAM Procedure
Theoretical and Computational Details of the Semivariogram
Let 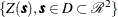 be a spatial random field (SRF) with n measured values
be a spatial random field (SRF) with n measured values 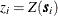 at respective locations
at respective locations 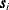 ,
, 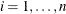 . You use the VARIOGRAM procedure because you want to gain insight into the spatial continuity and structure of
. You use the VARIOGRAM procedure because you want to gain insight into the spatial continuity and structure of 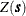 .
A good measure of the spatial continuity of
.
A good measure of the spatial continuity of 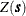 is defined by means of the variance of the difference
is defined by means of the variance of the difference 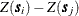 , where
, where 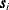 and
and 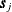 are locations in D. Specifically, if you consider
are locations in D. Specifically, if you consider 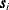 and
and 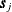 to be spatial increments such that
to be spatial increments such that 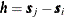 , then the variance function based on the increments
, then the variance function based on the increments 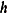 is independent of the actual locations
is independent of the actual locations 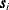 ,
, 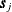 . Most commonly, the continuity measure used in practice is one half of this variance, better known as the semivariance function,
. Most commonly, the continuity measure used in practice is one half of this variance, better known as the semivariance function,
![\[ \gamma _ z(\bm {h}) = \frac{1}{2}{\mr{Var}}[Z(\bm {s}+\bm {h})-Z(\bm {s})] \]](images/statug_variogram0106.png)
or, equivalently,
![\[ \gamma _ z(\bm {h}) = \frac{1}{2} \left( \mr{E}\{ [Z(\bm {s}+\bm {h})-Z(\bm {s})]^2\} - \{ \mr{E}[Z(\bm {s}+\bm {h})]-\mr{E}[Z(\bm {s})]\} ^2 \right) \]](images/statug_variogram0107.png)
The plot of semivariance as a function of 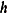 is the semivariogram. You might also commonly see the term semivariogram used instead of the term semivariance.
is the semivariogram. You might also commonly see the term semivariogram used instead of the term semivariance.
Assume that the SRF 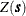 is free of nonrandom (or systematic) surface trends. Then, the expected value
is free of nonrandom (or systematic) surface trends. Then, the expected value ![$\mr{E}[Z(\bm {s})]$](images/statug_variogram0108.png) of
of 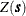 is a constant for all
is a constant for all 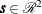 , and the semivariance expression is simplified to the following:
, and the semivariance expression is simplified to the following:
![\[ \gamma _ z(\bm {h}) = \frac{1}{2} \mr{E}\{ [Z(\bm {s}+\bm {h})-Z(\bm {s})]^2\} \]](images/statug_variogram0110.png)
Given the preceding assumption, you can compute an estimate 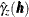 of the semivariance
of the semivariance 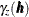 from a finite set of points in a practical way by using the formula
from a finite set of points in a practical way by using the formula
![\[ \hat{\gamma }_ z(\bm {h}) = \frac{1}{2 \mid N(\bm {h}) \mid }\sum _{N(\bm {h})}[Z(\bm {s}_ i)-Z(\bm {s}_ j)]^2 \]](images/statug_variogram0112.png)
where the sets 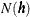 contain all the neighboring pairs at distance
contain all the neighboring pairs at distance 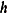 ,
,
![\[ N(\bm {h}) = \{ i,j: \bm {s}_ i-\bm {s}_ j = \bm {h}\} \]](images/statug_variogram0114.png)
and 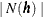 is the number of such pairs
is the number of such pairs 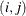 .
.
The expression for 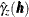 is called the empirical semivariance (Matheron 1963). This is the quantity that PROC VARIOGRAM computes, and its corresponding plot is the empirical semivariogram.
is called the empirical semivariance (Matheron 1963). This is the quantity that PROC VARIOGRAM computes, and its corresponding plot is the empirical semivariogram.
The empirical semivariance 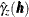 is also referred to as classical.
This name is used so that it can be distinguished from the robust semivariance estimate
is also referred to as classical.
This name is used so that it can be distinguished from the robust semivariance estimate 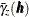 and the corresponding robust semivariogram.
The robust semivariance was introduced by Cressie and Hawkins (1980) to weaken the effect that outliers in the observations might have on the semivariance. It is described by Cressie (1993, p. 75) as
and the corresponding robust semivariogram.
The robust semivariance was introduced by Cressie and Hawkins (1980) to weaken the effect that outliers in the observations might have on the semivariance. It is described by Cressie (1993, p. 75) as
![\[ \bar{\gamma }_ z(\bm {h}) = \frac{\Psi ^4(\bm {h})}{2 [0.457 + 0.494/N(\bm {h})]} \]](images/statug_variogram0118.png)
In the preceding expression the parameter 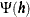 is defined as
is defined as
![\[ \Psi (\bm {h}) = \frac{1}{N(\bm {h})} \sum _{P_ iP_ j \in N(\bm {h})}[Z(\bm {s}_ i)-Z(\bm {s}_ j)]^{\frac{1}{2}} \]](images/statug_variogram0120.png)
According to Cressie (1985), the estimate 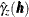 has approximate variance
has approximate variance
![\[ {\mr{Var}}[\hat{\gamma }_ z(\bm {h})] \simeq \frac{2[\gamma _ z(\bm {h})]^2}{N(\bm {h})} \]](images/statug_variogram0121.png)
This approximation is possible by assuming 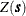 to be a Gaussian SRF, and by further assuming the squared differences in empirical semivariances to be uncorrelated for different
distances
to be a Gaussian SRF, and by further assuming the squared differences in empirical semivariances to be uncorrelated for different
distances 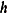 . Typically, semivariance estimates are correlated because of the underlying spatial correlation among the observations, and
also because the same observation pairs might be used for the estimation of more than one semivariogram point, as described
in the following subsections. Despite these restrictive assumptions, the approximate variance provides an idea about the semivariance
estimate variance and enables fitting of a theoretical model to the empirical semivariance; see the section Theoretical Semivariogram Model Fitting for more details about the fitting process.
. Typically, semivariance estimates are correlated because of the underlying spatial correlation among the observations, and
also because the same observation pairs might be used for the estimation of more than one semivariogram point, as described
in the following subsections. Despite these restrictive assumptions, the approximate variance provides an idea about the semivariance
estimate variance and enables fitting of a theoretical model to the empirical semivariance; see the section Theoretical Semivariogram Model Fitting for more details about the fitting process.
Note: If your data include a surface trend, then the empirical semivariance 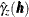 is not an estimate of the theoretical semivariance function
is not an estimate of the theoretical semivariance function 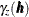 . Instead, rather than the spatial increments variance, it represents a different quantity known as pseudo-semivariance, and its corresponding plot is a pseudo-semivariogram.
In principle, pseudo-semivariograms do not provide measures of the spatial continuity. They can thus lead to misinterpretations
of the
. Instead, rather than the spatial increments variance, it represents a different quantity known as pseudo-semivariance, and its corresponding plot is a pseudo-semivariogram.
In principle, pseudo-semivariograms do not provide measures of the spatial continuity. They can thus lead to misinterpretations
of the 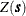 spatial structure, and are consequently unsuitable for the purpose of spatial prediction. For further information, see the
detailed discussion in the section Empirical Semivariograms and Surface Trends. Under certain conditions you might be able to gain some insight about the spatial continuity with a pseudo-semivariogram.
This case is presented in Analysis without Surface Trend Removal.
spatial structure, and are consequently unsuitable for the purpose of spatial prediction. For further information, see the
detailed discussion in the section Empirical Semivariograms and Surface Trends. Under certain conditions you might be able to gain some insight about the spatial continuity with a pseudo-semivariogram.
This case is presented in Analysis without Surface Trend Removal.
