The VARIOGRAM Procedure

Nested Models

When you try to represent an empirical semivariogram by fitting a theoretical model, you might find that using a combination of theoretical models results in a more accurate fit onto the empirical semivariance than using a single model. This is known as model nesting. The semivariance models that result as the sum of two or more semivariance structures are called nested models.

In general, a linear combination of permissible semivariance models produces a new permissible semivariance model. Nested models are based on this premise. You can include in a sum any combination of the models presented in Table 122.4. For example, a nested semivariance 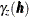$\gamma _{z}(\bm {h})$ that contains two structures, one exponential $\gamma _{z,\mr{EXP}}(\bm {h})$ and one spherical $\gamma _{z,\mr{SPH}}(\bm {h})$ , can be expressed as

$\gamma _{z}(\bm {h}) = \gamma _{z,\mr{EXP}}(\bm {h}) + \gamma _{z,\mr{SPH}}(\bm {h})$

If you have a nested model and a nugget effect, then the nugget effect 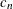$c_ n$ is a single parameter that is considered jointly for all the nested structures.

Nested models, anisotropic models, and the nugget effect increase the scope of theoretical models available. You can find additional discussion about these concepts in the section Theoretical Semivariogram Models in Chapter 67: The KRIGE2D Procedure.