The VARIOGRAM Procedure

Angle Classification

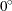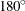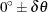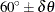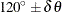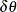Suppose you specify NDIRECTIONS=3 in the COMPUTE statement in PROC VARIOGRAM. This results in three angle classes defined by midpoint angles between $0^{\circ }$ and $180^{\circ }$ : $0^{\circ } \pm \delta \theta$ , $60^{\circ } \pm \delta \theta$ , and $120^{\circ } \pm \delta \theta$ , where $\delta \theta$ is the angle tolerance. If you do not specify an angle tolerance by using the ANGLETOLERANCE= option in the COMPUTE statement, the following default value is used:

$\delta \theta = \frac{180^{\circ }}{2 \times {\mr{NDIR}}}$

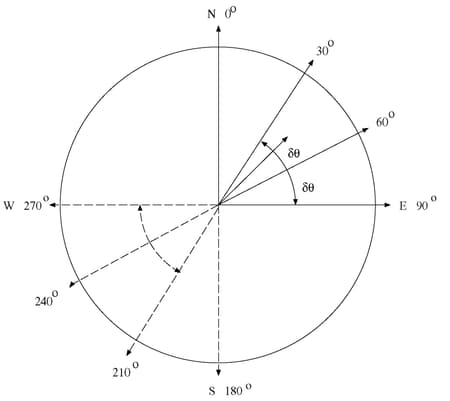
For example, if NDIRECTIONS=3, the default angle tolerance is 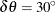$\delta \theta = 30^{\circ }$ . When the directed line segment 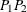$P_1P_2$ in Figure 122.19 is superimposed on the coordinate system that shows the angle classes, its angle is approximately 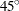$45^{\circ }$ , measured clockwise from north. In particular, it falls within 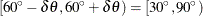$[60^{\circ } - \delta \theta , 60^{\circ } + \delta \theta )= [30^{\circ },90^{\circ })$ , the second angle class (Figure 122.20).

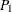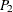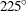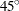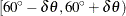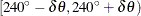Note: If the designated points $P_1$ and $P_2$ are labeled in the opposite order, the orientation is in the opposite direction—that is, approximately $225^{\circ }$ instead of approximately $45^{\circ }$ . This does not affect angle class selection; the angle classes $[60^{\circ } - \delta \theta , 60^{\circ } + \delta \theta )$ and $[240^{\circ } - \delta \theta , 240^{\circ } + \delta \theta )$ are the same.

Figure 122.20: Selected Pair 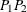$P_1P_2$ Falls within the Second Angle Class

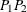If you specify an angle tolerance less than the default, such as ATOL=15 $^{\circ }$ , some point pairs might be excluded. For example, the selected point pair $P_1P_2$ in Figure 122.20, while closest to the 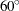$60^{\circ }$ axis, might lie outside 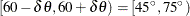$[60-\delta \theta ,60+\delta \theta )= [45^{\circ },75^{\circ })$ . In this case, the point pair 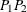$P_1P_2$ would be excluded from the semivariance computation. This setting can be desirable if you want to reduce interference between neighboring angles. An angle tolerance that is too small might result in too few point pairs in some distance classes for the empirical semivariance estimation (see also the discussion in the section Choosing the Size of Classes).

On the other hand, you can specify an angle tolerance greater than the default. This can result in a point pair being counted in more than one angle classes. This has a smoothing effect on the variogram and is useful when only a small amount of data is present or the available data are sparsely located. However, in cases of anisotropy the smoothing effect might have the side effect of amplifying weaker anisotropy in some direction and weakening stronger anisotropy in another (Deutsch and Journel 1992, p. 59).

Changes in the values of the BANDWIDTH= option have a similar effect. See the section Bandwidth Restriction for an explanation of how BANDWIDTH= functions.

An alternative way to specify angle classes and angle tolerances is with the DIRECTIONS statement. The DIRECTIONS statement is useful when angle classes are not equally spaced. When you use the DIRECTIONS statement, consider specifying the angle tolerance too. The default value of the angle tolerance is 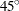$45^{\circ }$ when a DIRECTIONS statement is used instead of the NDIRECTIONS= option in the COMPUTE statement. This might not be appropriate for a particular set of angle classes. See the section DIRECTIONS Statement for more details.