The VARIOGRAM Procedure
Stationarity
In the combined presence of the previous two assumptions—that is, when ![$\mr{E}[Z(\bm {s})]$](images/statug_variogram0108.png) is constant and spatial increments define
is constant and spatial increments define 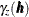 —the SRF
—the SRF 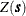 is characterized as intrinsically stationary (Cressie 1993, p. 40).
is characterized as intrinsically stationary (Cressie 1993, p. 40).
The expected value ![$\mr{E}[Z(\bm {s})]$](images/statug_variogram0108.png) is the first statistical moment of the SRF
is the first statistical moment of the SRF 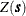 . The second statistical moment of the SRF
. The second statistical moment of the SRF 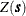 is the covariance
function between two points
is the covariance
function between two points 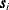 and
and 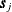 in
in 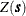 , and it is defined as
, and it is defined as
![\[ C_ z(\bm {s}_ i,\bm {s}_ j) = \mr{E} \left( \left[ Z(\bm {s}_ i)-\mr{E}[Z(\bm {s}_ i)] \right] \left[ Z(\bm {s}_ j)-\mr{E}[Z(\bm {s}_ j)] \right] \right) \]](images/statug_variogram0122.png)
When 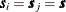 , the covariance expression provides the variance at
, the covariance expression provides the variance at  .
.
The assumption of a constant ![$\mr{E}[Z(\bm {s})]=m$](images/statug_variogram0124.png) means that the expected value is invariant with respect to translations of the spatial location
means that the expected value is invariant with respect to translations of the spatial location  . The covariance is considered invariant to such translations when it depends only on the distance
. The covariance is considered invariant to such translations when it depends only on the distance 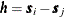 between any two points
between any two points 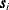 and
and 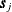 . If both of these conditions are true, then the preceding expression becomes
. If both of these conditions are true, then the preceding expression becomes
![\[ C_ z(\bm {s}_ i,\bm {s}_ j) = C_ z(\bm {s}_ i-\bm {s}_ j) = C_ z(\bm {h}) = \mr{E} \left( [Z(\bm {s})-m][Z(\bm {s}+\bm {h})-m] \right) \]](images/statug_variogram0125.png)
When both ![$\mr{E}[Z(\bm {s})]$](images/statug_variogram0108.png) and
and 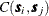 are invariant to spatial translations, the SRF
are invariant to spatial translations, the SRF 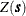 is characterized as second-order stationary (Cressie 1993, p. 53).
is characterized as second-order stationary (Cressie 1993, p. 53).
In a second-order stationary SRF the quantity 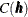 is the same for any two points that are separated by distance
is the same for any two points that are separated by distance 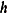 . Based on the preceding formula, for
. Based on the preceding formula, for 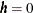 you can see that the variance is constant throughout a second-order stationary SRF. Hence, second-order stationarity is a
stricter condition than intrinsic stationarity.
you can see that the variance is constant throughout a second-order stationary SRF. Hence, second-order stationarity is a
stricter condition than intrinsic stationarity.
Under the assumption of second-order stationarity, the semivariance definition at the beginning of this section leads to the conclusion that
![\[ \gamma _ z(\bm {h}) = C(\bm {0}) - C(\bm {h}) \]](images/statug_variogram0128.png)
which relates the theoretical semivariance and covariance. Keep in mind that the empirical estimates of these quantities are not related in exactly the same way, as indicated in Schabenberger and Gotway (2005, section 4.2.1).
