The TRANSREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics
Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
MODEL Statement
- Families of Transformations
- Variable Expansions
- Nonoptimal Transformations
- Nonlinear Fit Transformations
- Optimal Transformations
- Other Transformations
- Transformation Options (t-options)
- Nonoptimal Transformation t-options
- Parameter t-options
- Spline t-options
- Penalized B-Spline t-options
- Class Variable t-options
- Box-Cox t-options
- Other t-options
- Algorithm Options (a-options)
The MODEL statement specifies the dependent and independent variables (dependents and independents, respectively) and specifies the transformation (transform) to apply to each variable. Only one MODEL statement can appear in PROC TRANSREG. The t-options are transformation options, and the a-options are algorithm options. The t-options provide details for the transformation; these depend on the transform chosen. The t-options are listed after a slash in the parentheses that enclose the variable list (either dependents or independents). The a-options control the algorithm used, details of iteration, details of how the intercept and coded variables are generated, and displayed output details. The a-options are listed after the entire model specification (the dependents, independents, transformations, and t-options) and after a slash. You can also specify the algorithm options in the PROC TRANSREG statement. When you specify the DESIGN o-option, dependents and an equal sign are not required. The operators *, |, and @ from the GLM procedure are available for interactions with the CLASS expansion and the IDENTITY transformation. They are used as follows:
Class(a * b ...
c | d ...
e | f ... @ n)
Identity(a * b ...
c | d ...
e | f ... @ n)
In addition, transformations and spline expansions can be crossed with classification variables as follows:
transform(var) * class(group) transform(var) | class(group)
See the section Types of Effects in Chapter 46: The GLM Procedure, for a description of the @, *, and | operators and see the section Model Statement Usage for information about how to use these operators in PROC TRANSREG. Note that nesting is not implemented in PROC TRANSREG.
The next three sections discuss the transformations available (transforms) (see the section Families of Transformations), the transformation options (t-options) (see the section Transformation Options (t-options)), and the algorithm options (a-options) (see the section Algorithm Options (a-options)).
Families of Transformations
In the MODEL statement, transform specifies a transformation in one of the following five families:
- Variable expansions
-
preprocess the specified variables, replacing them with more variables.
- Nonoptimal transformations
-
preprocess the specified variables, replacing each one with a single new nonoptimal, nonlinear transformation.
- Nonlinear fit transformations
-
preprocess the specified variable, replacing it with a smooth transformation, fitting one or more nonlinear functions through a scatter plot.
- Optimal transformations
-
replace the specified variables with new, iteratively derived optimal transformation variables that fit the specified model better than the original variable (except for contrived cases where the transformation fits the model exactly as well as the original variable).
- Other transformations
-
are the IDENTITY and SSPLINE transformations. These do not fit into the preceding categories.
The transformations and expansions listed in Table 117.2 are available in the MODEL statement.
Table 117.2: Transformation Families
|
Transformation |
Description |
|---|---|
|
Variable Expansions |
|
|
B-spline basis |
|
|
set of coded variables |
|
|
elliptical response surface |
|
|
circular response surface & PREFMAP |
|
|
piecewise polynomial basis |
|
|
quadratic response surface |
|
|
Nonoptimal Transformations |
|
|
inverse trigonometric sine |
|
|
exponential |
|
|
logarithm |
|
|
logit |
|
|
raises variables to specified power |
|
|
transforms to ranks |
|
|
Nonlinear Fit Transformations |
|
|
Box-Cox |
|
|
penalized B-splines |
|
|
noniterative smoothing spline |
|
|
Optimal Transformations |
|
|
linear |
|
|
monotonic, ties preserved |
|
|
monotonic B-spline |
|
|
optimal scoring |
|
|
B-spline |
|
|
monotonic, ties not preserved |
|
|
Other Transformations |
|
|
identity, no transformation |
|
|
iterative smoothing spline |
|
You can use any transformation with either dependent or independent variables (except the SMOOTH and PBSPLINE transformations, which can be used only with independent variables, and BOXCOX , which can be used only with dependent variables). However, the variable expansions are usually more appropriate for independent variables.
The transform is followed by a variable (or list of variables) enclosed in parentheses. Here is an example:
model log(y) = class(x);
This example finds a LOG
transformation of y and performs a CLASS
expansion of x. Optionally, depending on the transform, the parentheses can also contain t-options, which follow the variables and a slash. Here is an example:
model identity(y) = spline(x1 x2 / nknots=3);
The preceding statement finds SPLINE
transformations of x1 and x2. The NKNOTS=
t-option used with the SPLINE transformation specifies three knots. The identity(y) transformation specifies that y is not to be transformed.
The rest of this section provides syntax details for members of the five families of transformations listed at the beginning of this section. The t-options are discussed in the section Transformation Options (t-options).
Variable Expansions
PROC TRANSREG performs variable expansions before iteration begins. Variable expansions expand the original variables into
a typically larger set of new variables. The original variables are those that are listed in parentheses after transform, and they are sometimes referred to by the name of the transform. For example, in CLASS
(x1 x2), x1 and x2 are sometimes referred to as CLASS expansion variables or simply CLASS variables, and the expanded variables are referred
to as coded or sometimes "dummy" variables. Similarly, in POINT
(Dim1 Dim2), Dim1 and Dim2 are sometimes referred to as POINT variables.
The resulting variables are not transformed by the iterative algorithms after the initial preprocessing. Observations with missing values for these types of variables are excluded from the analysis.
The POINT , EPOINT , and QPOINT variable expansions are used in preference mapping analyses (also called PREFMAP, external unfolding, ideal point regression) (Carroll 1972) and for response surface regressions. These three expansions create circular, elliptical, and quadratic response or preference surfaces (see the section Point Models and Example 117.6). The CLASS variable expansion is used for main-effects ANOVA.
The following list provides syntax and details for the variable expansion transforms.
Nonoptimal Transformations
The nonoptimal transformations, like the variable expansions, are computed before the iterative algorithm begins. Nonoptimal transformations create a single new transformed variable that replaces the original variable. The new variable is not transformed by the subsequent iterative algorithms (except for a possible linear transformation with missing value estimation). The following list provides syntax and details for nonoptimal variable transformations.
Nonlinear Fit Transformations
Nonlinear fit transformations, like nonoptimal transformations, are computed before the iterative algorithm begins. Nonlinear fit transformations create a single new transformed variable that replaces the original variable and provides one or more smooth functions through a scatter plot. The new variable is not transformed by the subsequent iterative algorithms. The nonlinear fit transformations, unlike the nonoptimal transformations, use information in the other variables in the model to find the transformations. The nonlinear fit transformations, unlike the optimal transformations, do not minimize a squared-error criterion. The following list provides syntax and details for nonoptimal variable transformations.
Optimal Transformations
Optimal transformations are iteratively derived. Missing values for these types of variables can be optimally estimated (see the section Missing Values). The following list provides syntax and details for optimal transformations.
Other Transformations
Transformation Options (t-options)
If you use a nonoptimal, nonlinear fit, optimal, or other transformation, you can use t-options, which specify additional details of the transformation. The t-options are specified within the parentheses that enclose variables and are listed after a slash. You can use t-options with both the dependent and the independent variables. Here is an example of using just one t-option:
proc transreg; model identity(y)=spline(x / nknots=3); output; run;
The preceding statements find an optimal variable transformation (SPLINE ) of the independent variable, and they use a t-option to specify the number of knots (NKNOTS= ). The following is a more complex example:
proc transreg; model mspline(y / nknots=3)=class(x1 x2 / effects); output; run;
These statements find a monotone spline transformation (MSPLINE with three knots) of the dependent variable and perform a CLASS expansion with effects coding of the independents.
Table 117.3 summarizes the t-options available in the MODEL statement.
Table 117.3: Transformation Options
|
Option |
Description |
|---|---|
|
Nonoptimal Transformation |
|
|
Uses original mean and variance |
|
|
Parameter Specification |
|
|
Specifies miscellaneous parameters |
|
|
Specifies smoothing parameter |
|
|
Penalized B-Spline |
|
|
Uses Akaike’s information criterion |
|
|
Uses corrected AIC |
|
|
Uses cross validation criterion |
|
|
Uses generalized cross validation criterion |
|
|
Specifies smoothing parameter list or range |
|
|
Specifies a LAMBDA= range, not a list |
|
|
Uses Schwarz’s Bayesian criterion |
|
|
Spline |
|
|
Specifies the degree of the spline |
|
|
Spaces the knots evenly |
|
|
Specifies exterior knots |
|
|
Specifies the interior knots or break points |
|
|
Creates n knots |
|
|
CLASS Variable |
|
|
Specifies CLASS coded variable name prefix |
|
|
Specifies a deviations-from-means coding |
|
|
Specifies a deviations-from-means coding |
|
|
Specifies CLASS coded variable label prefix |
|
|
Specifies order of CLASS variable levels |
|
|
Specifies an orthogonal-contrast coding |
|
|
Specifies CLASS coded variable label separators |
|
|
Specifies a standardized-orthogonal coding |
|
|
Controls reference levels |
|
|
Box-Cox |
|
|
Specifies confidence interval alpha |
|
|
Specifies convenient lambda list |
|
|
Uses a convenient lambda |
|
|
Scales transformation using geometric mean |
|
|
Specifies power parameter list |
|
|
Other t-options |
|
|
Specifies operations occur after the expansion |
|
|
Specifies center before the analysis begins |
|
|
Renames variables |
|
|
Reflects the variable around the mean |
|
|
Specifies transformation standardization |
|
|
Standardizes before the analysis begins |
|
The following sections discuss the t-options available for nonoptimal, nonlinear fit, optimal, and other transformations.
Nonoptimal Transformation t-options
Parameter t-options
Spline t-options
The following t-options are available with the SPLINE , MSPLINE and PBSPLINE transformations and with the PSPLINE and BSPLINE expansions.
Penalized B-Spline t-options
The following t-options are available with the PBSPLINE transformation.
Class Variable t-options
Box-Cox t-options
The following t-options are available only with the BOXCOX transformation of the dependent variable (see the section Box-Cox Transformations and Example 117.2).
Other t-options
Algorithm Options (a-options)
This section discusses the options that can appear in the PROC TRANSREG or MODEL statement as a-options. They are listed after the entire model specification and after a slash. Here is an example:
proc transreg;
model spline(y / nknots=3)=log(x1 x2 / parameter=2)
/ nomiss maxiter=50;
output;
run;
In the preceding statements, NOMISS
and MAXITER=
are a-options. (SPLINE
and LOG
are transforms, and NKNOTS=
and PARAMETER=
are t-options.) The statements find a spline transformation with 3 knots on y and a base 2 logarithmic transformation on x1 and x2. The NOMISS
a-option excludes all observations with missing values, and the MAXITER=
a-option specifies the maximum number of iterations.
Table 117.4 summarizes the a-options available in the PROC TRANSREG or MODEL statement.
Table 117.4: Options Available in the PROC TRANSREG or MODEL Statement
|
Option |
Description |
|---|---|
|
Input Control |
|
|
Restarts iterations |
|
|
Specifies input observation type |
|
|
Method and Iterations |
|
|
Specifies minimum criterion change |
|
|
Specifies minimum data change |
|
|
Specifies maximum number of iterations |
|
|
Specifies iterative algorithm |
|
|
Specifies number of canonical variables |
|
|
Specifies no restrictions on smoothing models |
|
|
Specifies singularity criterion |
|
|
Attempts direct solution instead of iteration |
|
|
Missing Data Handling |
|
|
Fits each model individually (METHOD=MORALS) |
|
|
Includes monotone special missing values |
|
|
Excludes observations with missing values |
|
|
Unties special missing values |
|
|
Intercept and CLASS Variables |
|
|
Specifies CLASS coded variable name prefix |
|
|
Specifies CLASS coded variable label prefix |
|
|
Specifies no intercept or centering |
|
|
Specifies order of CLASS variable levels |
|
|
Controls output of reference levels |
|
|
Specifies CLASS coded variable label separators |
|
|
Control Displayed Output |
|
|
Specifies confidence limits alpha |
|
|
Displays parameter estimate confidence limits |
|
|
Displays model specification details |
|
|
Displays iteration histories |
|
|
Suppresses displayed output |
|
|
Prints the Box-Cox log likelihood table |
|
|
Displays the R square |
|
|
Suppresses the iteration histories |
|
|
Displays regression results |
|
|
Displays ANOVA table |
|
|
Shortens transformed variable labels |
|
|
Displays conjoint part-worth utilities |
|
|
Standardization |
|
|
Fits additive model |
|
|
Does not zero constant variables |
|
|
Specifies transformation standardization |
|
The following list provides details about these a-options. The a-options are available in the PROC TRANSREG or MODEL statement.
[41] This is a new feature in SAS/STAT 14.1. If you want other values from the CLL= list to be considered as in previous releases, you must specify those values in the LAMBDA= t-option.
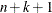
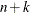






![\[ \mbox{minimum} + i((\mbox{maximum} - \mbox{minimum}) / (k + 1)) \]](images/statug_transreg0012.png)




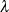









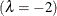


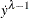
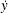
![\[ y = -(y-\bar{y}) + \bar{y} \]](images/statug_transreg0032.png)