The TRANSREG Procedure

MODEL <transform(dependents </ t-options >)><transform(dependents </ t-options >)…=> transform(independents </ t-options >)<transform(independents </ t-options >)…> </ a-options >;

Here are some examples of model statements:

linear regression
```
model identity(y) = identity(x);
```
a linear model with a nonlinear regression function
```
model identity(y) = spline(x / nknots=5);
```
multiple regression
```
model identity(y) = identity(x1-x5);
```

multiple regression with nonlinear transformations

model spline(y / nknots=3) = spline(x1-x5 / nknots=3);

multiple regression with nonlinear but monotone transformations
```
model mspline(y / nknots=3) = mspline(x1-x5 / nknots=3);
```

multivariate multiple regression

model identity(y1-y4) = identity(x1-x5);

canonical correlation

model identity(y1-y4) = identity(x1-x5) / method=canals;

redundancy analysis

model identity(y1-y4) = identity(x1-x5) / method=redundancy;

preference mapping, vector model (Carroll 1972)

model identity(Attrib1-Attrib3) = identity(Dim1-Dim2);

preference mapping, ideal point model (Carroll 1972)

model identity(Attrib1-Attrib3) = point(Dim1-Dim2);

preference mapping, ideal point model, elliptical (Carroll 1972)
```
model identity(Attrib1-Attrib3) = epoint(Dim1-Dim2);
```
preference mapping, ideal point model, quadratic (Carroll 1972)
```
model identity(Attrib1-Attrib3) = qpoint(Dim1-Dim2);
```

metric conjoint analysis

model identity(Subj1-Subj50) = class(a b c d e f / zero=sum);

nonmetric conjoint analysis

model monotone(Subj1-Subj50) = class(a b c d e f / zero=sum);

main effects, two-way interaction
```
model identity(y) = class(a|b);
```
less-than-full-rank model—main effects and two-way interaction are constrained to sum to zero
```
model identity(y) = class(a|b / zero=sum);
```
main effects and all two-way interactions
```
model identity(y) = class(a|b|c@2);
```
main effects and all two- and three-way interactions
```
model identity(y) = class(a|b|c);
```
main effects and only the b*c two-way interaction
```
model identity(y) = class(a b c b*c);
```

seven main effects, three two-way interactions

model identity(y) = class(a b c d e f g a*b a*c a*d);

deviations-from-means (effects or 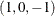$(1, 0, -1)$ ) coding, with an a reference level of ’1’ and a b reference level of ’2’
```
model identity(y) = class(a|b / deviations zero='1' '2');
```

cell-means coding (implicit intercept)

model identity(y) = class(a*b / zero=none);

reference cell model

model identity(y) = class(a|b / zero='1' '1');

reference line with change in line parameters

model identity(y) = class(a) | identity(x);

reference curve with change in curve parameters
```
model identity(y) = class(a) | spline(x);
```

separate curves and intercepts

model identity(y) = class(a / zero=none) | spline(x);

quantitative effects with interaction
```
model identity(y) = identity(x1 | x2);
```

separate quantitative effects with interaction within each cell

model identity(y) = class(a * b / zero=none) | identity(x1 | x2);