The TRANSREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics
Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Hypothesis Tests for Simple Univariate Models
If the dependent variable has one parameter (IDENTITY , LINEAR with no missing values, and so on) and if there are no monotonicity constraints, PROC TRANSREG fits univariate models, which can also be fit with a DATA step and PROC REG. This is illustrated with the following artificial data set:
data htex;
do i = 0.5 to 10 by 0.5;
x1 = log(i);
x2 = sqrt(i) + sin(i);
x3 = 0.05 * i * i + cos(i);
y = x1 - x2 + x3 + 3 * normal(7);
x1 = x1 + normal(7);
x2 = x2 + normal(7);
x3 = x3 + normal(7);
output;
end;
run;
Both PROC TRANSREG and PROC REG are run to fit the same polynomial regression model as follows:
proc transreg data=htex ss2 short; title 'Fit a Polynomial Regression Model with PROC TRANSREG'; model identity(y) = spline(x1); run; data htex2; set htex; x1_1 = x1; x1_2 = x1 * x1; x1_3 = x1 * x1 * x1; run; proc reg; title 'Fit a Polynomial Regression Model with PROC REG'; model y = x1_1 - x1_3; run; quit;
The ANOVA and regression tables from PROC TRANSREG are displayed in Figure 117.68. The ANOVA and regression tables from PROC REG are displayed in Figure 117.69. The SHORT a-option is specified with PROC TRANSREG to suppress the iteration history.
Figure 117.68: ANOVA and Regression Output from PROC TRANSREG
Figure 117.69: ANOVA and Regression Output from PROC REG
The PROC TRANSREG regression table differs in several important ways from the parameter estimate table produced by PROC REG.
The REG procedure displays standard errors and t statistics. PROC TRANSREG displays Type II sums of squares, mean squares, and F statistics. The difference is because the numerator degrees of freedom are not always 1, so t tests are not uniformly appropriate. When the degrees of freedom for variable 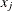 is 1, the following relationships hold between the standard errors
is 1, the following relationships hold between the standard errors 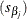 and the Type II sums of squares (
and the Type II sums of squares (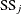 ):
):
![\[ s_{\beta _ j} = (\hat{\beta }^2_ j / F_ j)^{1/2} \]](images/statug_transreg0142.png)
and
![\[ \mr{SS}_ j = \hat{\beta }^2_ j \times \mr{MSE} / s^2_{\beta _ j} \]](images/statug_transreg0143.png)
PROC TRANSREG does not provide tests of the individual terms that go into the transformation. (However, it could if BSPLINE
or PSPLINE
had been specified instead of SPLINE
.) The test of spline(x1) is the same as the test of the overall model. The intercepts are different due to the different numbers of variables and
their standardizations.
In the next example, both x1 and x2 are transformed in the first PROC TRANSREG step, and PROC TRANSREG is used instead of a DATA step to create the polynomials
for PROC REG. Both PROC TRANSREG and PROC REG fit the same polynomial regression model. The following statements run PROC
TRANSREG and PROC REG and produce Figure 117.70 and Figure 117.71:
title 'Two-Variable Polynomial Regression'; proc transreg data=htex ss2 solve; model identity(y) = spline(x1 x2); run; proc transreg noprint data=htex maxiter=0; /* Use PROC TRANSREG to prepare input to PROC REG */ model identity(y) = pspline(x1 x2); output out=htex2; run; proc reg data=htex2; model y = x1_1-x1_3 x2_1-x2_3; test x1_1, x1_2, x1_3; test x2_1, x2_2, x2_3; run; quit;
Figure 117.70: Two-Variable Polynomial Regression Output from PROC TRANSREG
There are three iteration histories: one for the overall model and two for the two independent variables. The first PROC TRANSREG iteration history shows the R square of 0.17287 for the fit of the overall model. The second is for the following model:
model identity(y) = spline(x2);
This model excludes spline
(x1). The third iteration history is for the following model:
model identity(y) = spline(x1);
This model excludes spline(x2). The difference between the first and second R square times the total sum of squares is the model sum of squares for spline(x1):
![\[ (0.17287 - 0.15249) \times 224.143800 = 4.568165 \]](images/statug_transreg0144.png)
The difference between the first and third R square times the total sum of squares is the model sum of squares for spline(x2):
![\[ (0.17287 - 0.02604) \times 224.143800 = 32.911247 \]](images/statug_transreg0145.png)
Figure 117.71 displays the PROC REG results. The TEST statement in PROC REG tests the null hypothesis that the vector of parameters for
x1_1 x1_2 x1_3 is zero. This is the same test as the spline(x1) test used by PROC TRANSREG. Similarly, the PROC REG test that the vector of parameters for x2_1 x2_2 x2_3 is zero is the same as the PROC TRANSREG SPLINE
(x2) test. So for models with no monotonicity constraints and no dependent variable transformations, PROC TRANSREG provides little
more than a different packaging of standard least squares methodology.
Figure 117.71: Two-Variable Polynomial Regression Output from PROC REG
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Variable | Label | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | Intercept | 1 | 10.77824 | 7.55244 | 1.43 | 0.1771 |
| x1_1 | x1 1 | 1 | 0.40112 | 1.81024 | 0.22 | 0.8281 |
| x1_2 | x1 2 | 1 | 0.25652 | 1.66023 | 0.15 | 0.8796 |
| x1_3 | x1 3 | 1 | -0.11639 | 0.36775 | -0.32 | 0.7567 |
| x2_1 | x2 1 | 1 | -14.07054 | 12.50521 | -1.13 | 0.2809 |
| x2_2 | x2 2 | 1 | 5.95610 | 5.97952 | 1.00 | 0.3374 |
| x2_3 | x2 3 | 1 | -0.80608 | 0.87291 | -0.92 | 0.3726 |