The TRANSREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics
Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Point Models
The expanded set of independent variables generated from the POINT
, EPOINT
, and QPOINT
expansions can be used to perform ideal point regressions (Carroll 1972) and compute ideal point coordinates for plotting in a biplot (Gabriel 1981). The three types of ideal point coordinates can all be described as transformed coefficients. Assume that m independent variables are specified in one of the three point expansions. Let 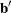 be a
be a 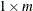 row vector of coefficients for these variables and one of the dependent variables. Let
row vector of coefficients for these variables and one of the dependent variables. Let 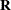 be a matrix created from the coefficients of the extra variables. When coordinates are requested with the MPC
, MEC
, or MQC
o-option,
be a matrix created from the coefficients of the extra variables. When coordinates are requested with the MPC
, MEC
, or MQC
o-option, 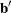 and
and 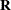 are created from multiple regression coefficients. When coordinates are requested with the CPC
, CEC
, or CQC
o-option,
are created from multiple regression coefficients. When coordinates are requested with the CPC
, CEC
, or CQC
o-option, 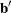 and
and 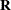 are created from canonical coefficients.
are created from canonical coefficients.
If you specify the POINT
expansion in the MODEL statement, 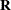 is an
is an  identity matrix times the coefficient for the sums of squares (_ISSQ_) variable. If you specify the EPOINT
expansion,
identity matrix times the coefficient for the sums of squares (_ISSQ_) variable. If you specify the EPOINT
expansion, 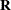 is an
is an  diagonal matrix of coefficients from the squared variables. If you specify the QPOINT
expansion,
diagonal matrix of coefficients from the squared variables. If you specify the QPOINT
expansion, 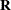 is an
is an  symmetric matrix of coefficients from the squared variables on the diagonal and crossproduct variables off the diagonal.
The MPC
, MEC
, MQC
, CPC
, CEC
, and CQC
ideal point coordinates are defined as
symmetric matrix of coefficients from the squared variables on the diagonal and crossproduct variables off the diagonal.
The MPC
, MEC
, MQC
, CPC
, CEC
, and CQC
ideal point coordinates are defined as 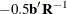 . When
. When 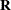 is singular, the ideal point coordinates are infinitely far away and are set to missing, so you should try a simpler version
of the model. The version that is simpler than the POINT
model is the vector model, where no extra variables are created. In the vector model, designate all independent variables
as IDENTITY
. Then draw vectors from the origin to the COEFFICIENTS
points.
is singular, the ideal point coordinates are infinitely far away and are set to missing, so you should try a simpler version
of the model. The version that is simpler than the POINT
model is the vector model, where no extra variables are created. In the vector model, designate all independent variables
as IDENTITY
. Then draw vectors from the origin to the COEFFICIENTS
points.
Typically, when you request ideal point coordinates, the MODEL statement should consist of a single transformation for the dependent variables (usually IDENTITY , MONOTONE , or MSPLINE ) and a single expansion for the independent variables (one of POINT , EPOINT , or QPOINT ).