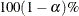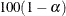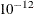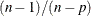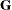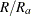The SURVEYPHREG Procedure

MODEL Statement

MODEL response <*censor (list)> = effects </ options>;

The MODEL statement identifies the variable to be used as the failure time variable, the optional censoring variable, and the explanatory effects, including covariates, main effects, and interactions; see the section Specification of Effects in Chapter 46: The GLM Procedure, for more information. A note of caution: specifying the effect T*A in the MODEL statement, where T is the time variable and A is a CLASS variable, does not make the effect time-dependent. You must specify exactly one MODEL statement.

The MODEL statement allows one response variable. In the MODEL statement, the failure time variable precedes the equal sign. This can optionally be followed by an asterisk, the name of the censoring variable, and a list of censoring values (separated by blanks or commas if there is more than one) enclosed in parentheses. If the censoring variable takes on one of these values, the corresponding failure time is considered to be censored. The variables following the equal sign are the explanatory variables (sometimes called independent variables or covariates) for the model.

The censoring variable must be numeric. The failure time variable must contain nonnegative values. Any observation with a negative failure time is excluded from the analysis, as is any observation with a missing value for any of the variables listed in the MODEL statement. See Missing Values for details.

Table 113.6 summarizes the options available in the MODEL statement, which can be specified after a slash (/).

Table 113.6: MODEL Statement Options

Option	Description
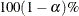ALPHA=	Specifies $\alpha$ for the $100(1-\alpha )\%$ confidence limits
CLPARM	Computes confidence limits for regression parameters
COVB	Displays covariance matrix
DF=	Specifies the denominator degrees of freedom
HESS	Displays the Hessian matrix
INVHESS	Displays the inverse of the Hessian matrix
RISKLIMITS	Computes confidence limits for the exponentials of the regression parameters
SERATIO=	Computes the ratio of two standard errors for the regression coefficients
SINGULAR=	Specifies tolerance for testing singularity
TIES=	Specifies the method of handling ties in failure times
VADJUST=	Specifies a variance adjustment factor
VARRATIO=	Computes the ratio of two variances for the regression coefficients

ALPHA= $\alpha$

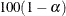sets the level of the confidence limits for the estimated regression parameters and the hazard ratios. The value of alpha must be between 0 and 1, and the default is 0.05. A confidence level of $\alpha$ produces $100(1-\alpha )$ % confidence limits. The default of ALPHA=0.05 produces 95% confidence limits.

The ALPHA= option has no effect unless you also specify the CLPARM or RISKLIMITS option.

CLPARM

produces confidence limits for regression parameters of Cox proportional hazards models. You can specify the confidence coefficient by using the ALPHA= option. Classification main effects that use parameterizations other than REF, EFFECT, or GLM are ignored. For more information, see the section Confidence Intervals.

COVB

displays the estimated covariance matrix of the parameter estimates.

DF=value | keyword <(value)>

specifies the denominator degrees of freedom for hypothesis tests, specifies the degrees of freedom for confidence limits, and requests adjustments to the Wald test statistics. If you specify a value, it must be a nonnegative number.

In the description that follows, d denotes the usual degrees of freedom computed from the survey data by using the number of strata, clusters, or replicate weights. For more information, see the section Degrees of Freedom.

By default, DF=PARMADJ when you use the Taylor series linearized variance estimator, and DF=DESIGN when you use the replication variance estimator. Alternatively, you can specify a nonnegative value for the degrees of freedom, or you can specify one of the following keywords:

ALLREPS: computes the denominator degrees of freedom for replication methods by using the total number of replicate samples. By default, PROC SURVEYPHREG computes the denominator degrees of freedom based on the number of replicate samples that are used. Some replicate samples might not be usable, in the sense that they cannot be used for variance estimation because of factors such as inestimability or nonconvergence. These replicate samples are not accounted for in the denominator degrees of freedom unless you specify DF=ALLREPS. For more information, see the section Degrees of Freedom.
DESIGN: computes the denominator degrees of freedom as d. When you specify DF=DESIGN, the corresponding Wald F statistics do not account for the number of parameters in the model. This option is useful if you do not want to apply the adjustment described in Korn and Graubard (1999, p. 93). For more information, see the section Testing the Global Null Hypothesis.
DESIGN (value): computes the denominator degrees of freedom as value. When you specify DF=DESIGN (value), the corresponding Wald F statistics do not account for the number of parameters in the model. This option is useful if you do not want to apply the adjustment described in Korn and Graubard (1999, p. 93) and you want to specify the denominator degrees of freedom. You might want to specify a denominator degrees of freedom other than d for reasons such as missing values or domain estimation for relatively small domains. For more information, see the section Testing the Global Null Hypothesis.
DESIGNADJ: computes the denominator degrees of freedom as d. When you specify DF=DESIGNADJ, the corresponding Wald F statistics account for the number of parameters in the model. This option is useful if you are fitting a model that has many parameters relative to d but you want to use d as the denominator degrees of freedom. For more information, see the section Testing the Global Null Hypothesis.
NONE: specifies the denominator degrees of freedom to be infinite. This option is useful if you want to compute chi-square tests and normal confidence intervals. For more information, see the section Testing the Global Null Hypothesis.
PARMADJ: computes the denominator degrees of freedom as d minus the number of nonsingular parameters plus 1. When you specify DF=PARMADJ, the corresponding Wald F statistics account for the number of parameters in the model. This option is useful if you are fitting a model that has many parameters relative to d. For more information, see the section Testing the Global Null Hypothesis.
PARMADJ (value): computes the denominator degrees of freedom as value. When you specify DF=PARMADJ (value), the corresponding Wald F statistics account for the number of parameters in the model. This option is useful if you are fitting a model with that has parameters relative to d and you want to specify the denominator degrees of freedom. You might want to specify the denominator degrees of freedom for reasons such as missing values or domain estimation for relatively small domains. For more information, see the section Testing the Global Null Hypothesis.

HESS

displays the last evaluation of the Hessian matrix.

INVHESS

displays the inverse of the Hessian matrix that is evaluated at the estimated regression parameters.

RISKLIMITS RL

produces confidence limits for hazard ratios and related quantities. For more information, see the section Hazard Ratios. You can specify the confidence coefficient by using the ALPHA= option. You must take great care with any interpretation of the estimates and their confidence limits if interaction effects are involved in the model or if parameterizations other than REF, EFFECT, or GLM are used.

SERATIO=ALL | MODEL | IND

computes the ratio of two standard errors for the regression parameters. The standard error in the numerator uses the complete design information that you specify. You can specify the following options to compute different standard errors for the denominator:

ALL: requests both MODEL and IND standard error ratios.
MODEL: computes the standard errors in the denominator as the square root of the diagonals of the inverse Hessian matrix evaluated at the estimated regression parameters. For more information, see the section Variance Ratios and Standard Error Ratios.
IND: computes the standard errors in the denominator by ignoring stratification and clustering. For more information, see the section Variance Ratios and Standard Error Ratios.

SINGULAR=value

specifies the singularity criterion for determining linear dependencies in the set of explanatory variables. The default value is 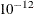$10^{-12}$ .

TIES=method

specifies how to handle ties in the failure time. You can specify the following methods:

BRESLOW: uses the approximate partial likelihood of Breslow (1974).
EFRON: uses the approximate partial likelihood of Efron (1977).

If there are no ties, both methods result in the same likelihood and yield identical estimates. By default, TIES=BRESLOW, which is the most efficient method when there are no ties.

VADJUST=DF | PARMADJ | NONE | AVGREPSS

specifies variance adjustment factors. You can specify the following keywords:

DF PARMADJ: requests the degrees-of-freedom adjustment $(n-1)/(n-p)$ in the computation of the matrix $\mb{G}$ for the Taylor series linearization variance estimation .
NONE: excludes the degrees-of-freedom adjustment $(n-1)/(n-p)$ from the computation of the matrix $\mb{G}$ for the Taylor series linearization variance estimation . By default, VADJUST=NONE.
AVGREPSS: use the average sum of squares from all the usable replicate samples for the unusable replicates. This option is applicable only for the jackknife replication method. VADJUST=AVGREPSS multiplies the default jackknife variance estimator by the factor $R/R_ a$ , where $R_ a$ is the number of usable replicates and R is the total number of replicates. For more information, see the section Variance Adjustment Factors.

VARRATIO=ALL | MODEL | IND

computes the ratio of two variances for the regression parameters. The variance in the numerator uses the complete design information. You can specify the following options to compute different variances for the denominator:

ALL: requests both MODEL and IND variance ratios.
MODEL: computes the variances in the denominator as the diagonals of the inverse Hessian matrix evaluated at the estimated regression parameters. For more information, see the section Variance Ratios and Standard Error Ratios.
IND: computes the variances in the denominator by ignoring stratification and clustering. For more information, see the section Variance Ratios and Standard Error Ratios.