The SURVEYPHREG Procedure

Testing the Global Null Hypothesis

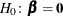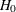The following statistics are available to test the global null hypothesis $H_{0}\colon {\bbeta }=\Strong{0}$. Let d be the usual degrees of freedom computed from the survey data by using the number of strata, clusters, or replicate weights; and let p be the number of estimable parameters in the null hypothesis $H_0$. For more information about computing d, see the section Degrees of Freedom.

The likelihood ratio test is expressed as

\[ \chi ^{2}_{\mr{LR}}=2 \left[ \log \left\{ \text {L} (\hat{\bbeta }) \right\} - \log \left\{ \text {L} (\mb{0}) \right\} \right] \]

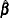where L($\cdot $) denotes the partial pseudo-likelihood described in the section Partial Likelihood Function for the Cox Model and $\hat{\bbeta }$ denotes the estimated regression parameters. The p-value is computed by using a chi-square distribution with p degrees of freedom. The likelihood ratio statistic is sensitive to the scaling of the weights. The usual assumptions that are required for a likelihood ratio test do not hold for the pseudo-likelihood that is used by PROC SURVEYPHREG (Rao, Scott, and Skinner 1998), leading to other methods of testing the global null hypothesis, such as the Wald test discussed in the following paragraph.

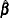The Wald test uses the variance estimator that accounts for complex sampling such as stratification, clustering, and unequal weighting. Let $Q=\hat{\bbeta }’ \left[\widehat{\mb{V}}(\hat{\bbeta }) \right]^{-1} \hat{\bbeta }$, where $\hat{\bbeta }$ is the estimated regression parameters and 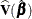$\widehat{\mb{V}}(\hat{\bbeta })$ is the estimated covariance matrix for 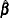$\hat{\bbeta }$. You can request the Wald tests that are described in the following table by using the DF= option in the MODEL statement.

     

Numerator

Denominator

Value of DF=

Test Request

Test Statistic

Degrees of Freedom

Degrees of Freedom

NONE

Chi-square

Q

p

$\infty $

v

Customized F

vQ/pd

p

v

DESIGN

Unadjusted F

Q/p

p

d

DESIGN (v)

Unadjusted F

Q/p

p

v

PARMADJ

Adjusted F

(d–p+1)Q/pd

p

d–p+1

PARMADJ (v)

Adjusted F

(v-p+1)Q/pv

p

v-p+1

DESIGNADJ

Adjusted F

(d–p+1)Q/pd

p

d