The SURVEYPHREG Procedure
- Overview
- Getting Started
-
Syntax
PROC SURVEYPHREG StatementBY StatementCLASS StatementCLUSTER StatementDOMAIN StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementProgramming StatementsREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement -
DetailsNotation and EstimationFailure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelSpecifying the Sample DesignMissing ValuesVariance EstimationDomain AnalysisHypothesis Tests, Confidence Intervals, and ResidualsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
-
Examples
- References
Failure Time Distribution
Let T be a nonnegative random variable that represents the failure time of an individual from a homogeneous superpopulation. The survival distribution function (also known as the survivor function) of T is written as
![\[ S(t)=\mr{Pr}(T \geq t) \]](images/statug_surveyphreg0057.png)
A mathematically equivalent way of specifying the distribution of T is through its hazard function. The hazard function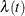 
specifies the instantaneous failure rate at t. If T is a continuous random variable, 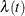is expressed as
![\[ \lambda (t)= \lim _{\Delta t \rightarrow 0^{+} } \frac{ \mr{Pr}(t \leq T < t + \Delta t\ |\ T \geq t) }{ \Delta t } = \frac{f(t)}{S(t)} \]](images/statug_surveyphreg0059.png)
where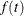 
is the probability density function of T.