The SURVEYPHREG Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYPHREG StatementBY StatementCLASS StatementCLUSTER StatementDOMAIN StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementProgramming StatementsREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement
PROC SURVEYPHREG StatementBY StatementCLASS StatementCLUSTER StatementDOMAIN StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementProgramming StatementsREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement -
Details
 Notation and EstimationFailure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelSpecifying the Sample DesignMissing ValuesVariance EstimationDomain AnalysisHypothesis Tests, Confidence Intervals, and ResidualsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Notation and EstimationFailure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelSpecifying the Sample DesignMissing ValuesVariance EstimationDomain AnalysisHypothesis Tests, Confidence Intervals, and ResidualsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Notation and Estimation
Let 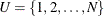 be the set of indices and let
be the set of indices and let 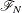 be the set of values for a finite population of size N. The survival time of each member of the finite population is assumed
to follow its own hazard function,
be the set of values for a finite population of size N. The survival time of each member of the finite population is assumed
to follow its own hazard function, 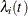 , expressed as
, expressed as
![\[ \lambda _{i}(t)=\lambda (t;{\bZ }_{i}(t)) = {\lambda _0}(t) \ \exp ({\bZ }’_{i}(t)\bbeta ) \]](images/statug_surveyphreg0002.png)
where 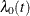 is an arbitrary and unspecified baseline hazard function,
is an arbitrary and unspecified baseline hazard function, 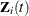 is the vector of explanatory variables for the ith unit at time t, and
is the vector of explanatory variables for the ith unit at time t, and 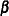 is the vector of unknown regression parameters that are associated with the explanatory variables. The vector
is the vector of unknown regression parameters that are associated with the explanatory variables. The vector 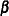 is assumed to be the same for all individuals.
is assumed to be the same for all individuals.
The partial likelihood function introduced by Cox (1972, 1975) eliminates the unknown baseline hazard 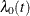 and accounts for censored survival times. If the entire population is observed, then this partial likelihood can be used
to estimate
and accounts for censored survival times. If the entire population is observed, then this partial likelihood can be used
to estimate 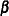 . Let
. Let 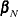 be the desired estimator.
Assuming a working model with uncorrelated responses,
be the desired estimator.
Assuming a working model with uncorrelated responses, 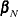 is obtained by maximizing the partial log likelihood,
is obtained by maximizing the partial log likelihood,
![\[ l(\bbeta ) = \sum _{i \in U} \log \biggl \{ \text {L}(\bbeta ; {\bZ }_ i(t), t_ i) \biggr \} \]](images/statug_surveyphreg0036.png)
with respect to 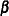 , where L
, where L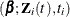 is Cox’s partial likelihood function.
is Cox’s partial likelihood function.
Assume that probability sample A is selected from the finite population U and 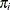 is the selection probability for unit i. Further assume that covariates
is the selection probability for unit i. Further assume that covariates 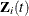 and survival time
and survival time 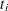 are available for every unit in the sample A. An estimator of the finite population log likelihood is
are available for every unit in the sample A. An estimator of the finite population log likelihood is
![\[ l_\pi (\bbeta ) = \sum _{i \in A} \pi _ i^{-1} \log \biggl \{ \text {L}(\bbeta ; {\bZ }_ i(t), t_ i) \biggr \} \]](images/statug_surveyphreg0040.png)
See Partial Likelihood Function for the Cox Model for more details.
A sample-based estimator 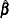 for the finite population quantity
for the finite population quantity 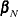 can be obtained by maximizing the partial pseudo-log-likelihood
can be obtained by maximizing the partial pseudo-log-likelihood 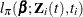 with respect to
with respect to 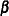 . The design-based variance for
. The design-based variance for 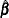 is obtained by assuming the set of finite population values
is obtained by assuming the set of finite population values 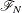 as fixed. For more information about maximum pseudo-likelihood estimators and other inferential approaches for survey data,
see Kish and Frankel (1974); Godambe and Thompson (1986); Pfeffermann (1993), Korn and Graubard (1999, chapter 3), Chambers and Skinner (2003, chapter 2), and Fuller (2009, section 6.5). Maximum pseudo-likelihood estimators and their properties for Cox’s proportional hazards model for survey
data are discussed in Binder (1990, 1992); Lin and Wei (1989); Lin (2000); Boudreau and Lawless (2006).
as fixed. For more information about maximum pseudo-likelihood estimators and other inferential approaches for survey data,
see Kish and Frankel (1974); Godambe and Thompson (1986); Pfeffermann (1993), Korn and Graubard (1999, chapter 3), Chambers and Skinner (2003, chapter 2), and Fuller (2009, section 6.5). Maximum pseudo-likelihood estimators and their properties for Cox’s proportional hazards model for survey
data are discussed in Binder (1990, 1992); Lin and Wei (1989); Lin (2000); Boudreau and Lawless (2006).
Without loss of generality, the rest of this section uses indices for stratified clustered designs. For a stratified clustered sample design, observations are represented by a matrix
![\[ (\mb{w, t,} \bDelta \mb{, Z}) = (w_{hij}, t_{hij}, \Delta _{hij}, \mb{z}_{hij}) \]](images/statug_surveyphreg0042.png)
where
-
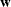 denotes the vector of sampling weights
denotes the vector of sampling weights
-
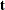 denotes the event time variable
denotes the event time variable
-
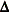 denotes the event indicator
denotes the event indicator
-
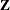 denotes the
denotes the 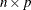 matrix of auxiliary information
matrix of auxiliary information
-
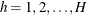 is the stratum index
is the stratum index
-
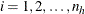 is the cluster index within stratum h
is the cluster index within stratum h
-
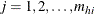 is the unit index within cluster i of stratum h
is the unit index within cluster i of stratum h
-
p is the total number of parameters
-
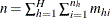 is the total number of observations in the sample
is the total number of observations in the sample
-
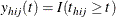 , where
, where 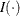 is an indicator function
is an indicator function
-
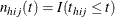 , where
, where 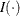 is an indicator function
is an indicator function
Let 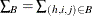 denote the summation over the set of indices such that the observation unit j in PSU i and stratum h belongs to the index set B. Typically, B is the set of all population indices that are in the sample, the risk set, or the set of all units with a failure.
denote the summation over the set of indices such that the observation unit j in PSU i and stratum h belongs to the index set B. Typically, B is the set of all population indices that are in the sample, the risk set, or the set of all units with a failure.
The first-stage sampling rate (fraction of PSUs selected for the sample) is denoted by 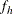 . The first-stage sampling rate is used in Taylor series variance estimation. You can specify the stratum sampling rates with
the RATE=
option. Or if you specify population totals with the TOTAL=
option, PROC SURVEYFREQ computes
. The first-stage sampling rate is used in Taylor series variance estimation. You can specify the stratum sampling rates with
the RATE=
option. Or if you specify population totals with the TOTAL=
option, PROC SURVEYFREQ computes 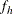 as the ratio of stratum sample size to the stratum total, in terms of PSUs. See the section Population Totals and Sampling Rates for details. If you do not specify the RATE= option or the TOTAL= option, then the procedure assumes that the stratum sampling
rates
as the ratio of stratum sample size to the stratum total, in terms of PSUs. See the section Population Totals and Sampling Rates for details. If you do not specify the RATE= option or the TOTAL= option, then the procedure assumes that the stratum sampling
rates 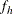 are negligible and does not use a finite population correction when computing variances.
are negligible and does not use a finite population correction when computing variances.