The SURVEYPHREG Procedure
- Overview
- Getting Started
-
Syntax
PROC SURVEYPHREG StatementBY StatementCLASS StatementCLUSTER StatementDOMAIN StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementProgramming StatementsREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement -
DetailsNotation and EstimationFailure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelSpecifying the Sample DesignMissing ValuesVariance EstimationDomain AnalysisHypothesis Tests, Confidence Intervals, and ResidualsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
-
Examples
- References
Model Fit Statistics
Suppose the model contains p estimable parameters. Then the following two criteria are displayed for model fit statistics:
-
–2 log likelihood:
![\[ -2\mbox{ Log L}=-2 \log (L(\hat{\bbeta })) \]](images/statug_surveyphreg0132.png)
where
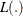is a partial pseudo-likelihood function for the corresponding TIES= option as described in the section Partial Likelihood Function for the Cox Model, and 
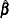is the maximum pseudo-log-likelihood estimate of the proportional hazards regression coefficients.
-
Akaike’s information criterion (AIC):
![\[ \mbox{AIC}=-2\mbox{ Log L}+2p \]](images/statug_surveyphreg0134.png)
The AIC statistic provides a different way of adjusting the log-likelihood statistic for the number of estimable parameters in the model.
Neither of these criteria is adjusted for the complex sample design, and both criteria are sensitive to the scale of the weights.