The SURVEYPHREG Procedure
- Overview
- Getting Started
-
Syntax
PROC SURVEYPHREG StatementBY StatementCLASS StatementCLUSTER StatementDOMAIN StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementProgramming StatementsREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement -
DetailsNotation and EstimationFailure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelSpecifying the Sample DesignMissing ValuesVariance EstimationDomain AnalysisHypothesis Tests, Confidence Intervals, and ResidualsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
-
Examples
- References
Hazard Ratios
The hazard ratio for a quantitative effect with regression coefficient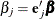 
is defined as exp
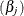, where 
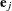denotes the jth unit vector. In general, a log-hazard ratio can be written as 
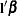, a linear combination of the regression coefficients, and the hazard ratio exp
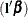is obtained by replacing 
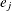with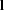 
.
The confidence intervals for hazard ratios are obtained by exponentiating the confidence limits of the corresponding linear
combination. Thus, the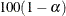 
confidence limits are
![\[ \exp \left( \mb{e}_ j’ \hat{\bbeta } \pm t_{\mi{df},\alpha /2} \sqrt {\mb{e}_ j’\hat{\mb{V}}(\hat{\bbeta })\mb{e}_ j} \right) \]](images/statug_surveyphreg0150.png)
where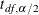 
is the 
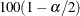percentile point of the t distribution with df degrees of freedom. See the section Degrees of Freedom for more information about df. If you use the DF=NONE
option in the MODEL statement, then the procedure uses the 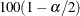percentile point of the standard normal distribution.