The ROBUSTREG Procedure

Leverage-Point and Outlier Detection

The regular variable LEVERAGE is defined as

\[ {\mbox{LEVERAGE }} = \left\{ \begin{array}{ll} 0 & {\mbox{ if }} \mr{RD}(\mb{x}_ i) \leq C(p) \\ 1 & {\mbox{ otherwise }} \end{array} \right. \]

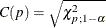where $C(p) = {\sqrt {\chi ^2_{p; 1-\alpha }}}$ is the cutoff value. 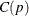$C(p)$ can be set by using the leverage CUTOFF= option, and $\alpha $ can be set by using the leverage CUTOFFALPHA= option.

If projected robust distances are computed for a data set that has a low-dimensional structure, the default cutoff value is 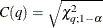$C(q) = {\sqrt {\chi ^2_{q; 1-\alpha }}}$, where q is the dimensionality of the low-dimensional space. LEVERAGE is then defined as

\[ {\mbox{LEVERAGE }} = \left\{ \begin{array}{ll} 0 & {\mbox{ if POD}}(\mb{x}_ i)=0 {\mbox{ and PRD}}(\mb{x}_ i) \leq C(q) \\ 1 & {\mbox{ if POD}}(\mb{x}_ i)=0 {\mbox{ and PRD}}(\mb{x}_ i)>C(q) {\mbox{ (called in-plane leverage)}}\\ 1 & {\mbox{ if POD}}(\mb{x}_ i)>0 {\mbox{ (called off-plane leverage)}}\\ \end{array} \right. \]

where POD is the projected off-plane distance and PRD denotes the projected robust distance. You can specify a cutoff value by using the CUTOFF= or CUTOFFALPHA= suboption of the LEVERAGE option in the MODEL statement.

Residuals 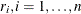$ r_ i, i=1,\ldots ,n$, based on robust regression estimates are used to detect vertical outliers. The variable OUTLIER is defined as

\[ {\mbox{OUTLIER }} = \left\{ \begin{array}{ll} 0 & {\mbox{ if }} |r_ i| \leq k{\hat\sigma } \\ 1 & {\mbox{ otherwise }} \end{array} \right. \]

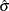where ${\hat\sigma }$ is the estimated scale in the model and the multiplier 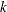$ k$ of the cutoff value is specified by the CUTOFF= option in the MODEL statement. By default, k = 3.

An ODS table called Diagnostics contains the LEVERAGE and OUTLIER variables.