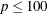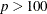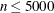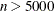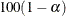The QUANTREG Procedure

PROC QUANTREG Statement

PROC QUANTREG <options>;

The PROC QUANTREG statement invokes the QUANTREG procedure. Table 95.1 summarizes the options available in the PROC QUANTREG statement.

Table 95.1: PROC QUANTREG Statement Options

Option	Description
ALGORITHM=	Specifies an algorithm to estimate the regression parameters
ALPHA=	Specifies the level of significance
CI=	Specifies a method to compute confidence intervals
DATA=	Specifies the input SAS data set
INEST=	Specifies an input SAS data set that contains initial estimates
NAMELEN=	Specifies the length of effect names
ORDER=	Specifies the order in which to sort classification variables
OUTEST=	Specifies an output SAS data set containing the parameter estimates
PLOT	Specifies options that control details of the plots

You can specify the following options in the PROC QUANTREG statement.

ALGORITHM=algorithm <( suboptions )>

specifies an algorithm for estimating the regression parameters.

You can specify one of the following four algorithms:

SIMPLEX <suboption>

uses the simplex algorithm to estimate the regression parameters. You can specify the following suboption:

MAXSTATIONARY=m: requests that the algorithm terminate if the objective function has not improved for m consecutive iterations. By default, m = 1000.

INTERIOR <( suboptions )>

uses the interior point algorithm to estimate the regression parameters. You can specify the following suboptions:

KAPPA=value: specifies the step-length parameter for the interior point algorithm. The value should be between 0 and 1. The larger the value, the faster the algorithm. However, numeric instability can occur as the value approaches 1. By default, KAPPA=0.99995. For more information, see the section Interior Point Algorithm.
MAXIT=m: sets the maximum number of iterations for the interior point algorithm. By default, MAXIT=1000.
TOLERANCE=value: specifies the tolerance for the convergence criterion of the interior point algorithm. By default, TOLERANCE=1E–8. The QUANTREG procedure uses the duality gap as the convergence criterion. For more information, see the section Interior Point Algorithm.

You can also use the PERFORMANCE statement to enable parallel computing when multiple processors are available in the hardware.

IPM <( suboptions )>

uses the efficient interior point algorithm to estimate the regression parameters. You can specify the following suboptions:

MAXIT=m: sets the maximum number of iterations for the efficient interior point algorithm. By default, MAXIT=1000.
TOLERANCE=value: specifies the tolerance for the convergence criterion of the efficient interior point algorithm. The QUANTREG procedure uses the complementarity value as the convergence criterion. By default, TOLERANCE=1E–8.

SMOOTH <suboption>

uses the smoothing algorithm to estimate the regression parameters. You can specify the following suboption:

RRATIO=value: specifies the reduction ratio for the smoothing algorithm. This ratio is used to reduce the threshold of the smoothing algorithm. The value should be between 0 and 1. In theory, the smaller the value, the faster the smoothing algorithm. However, in practice, the optimal ratio is quite dependent on the data. For more information, see the section Smoothing Algorithm.

The default algorithm depends on the number of observations (n) and the number of covariates (p) in the model estimation. See Table 95.2 for the relevant defaults.

Table 95.2: The Default Estimation Algorithm

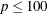
	$p\le 100$	$p>100$
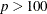
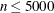
$n \le 5000$	SIMPLEX	SMOOTH
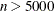
$n > 5000$	INTERIOR	SMOOTH

ALPHA=value

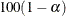specifies the level of significance $\alpha$ for $100(1-\alpha )$ % confidence intervals for regression parameters. The value must be between 0 and 1. The default is ALPHA=0.05, which corresponds to a 0.95 confidence interval.

CI=NONE | RANK | SPARSITY<(BF | HS)></IID> | RESAMPLING<(NREP=n)>

specifies a method for computing confidence intervals for regression parameters. When you specify CI=SPARSITY or CI=RESAMPLING, the QUANTREG procedure also computes standard errors, t values, and p-values for regression parameters.

Table 95.3 summarizes these methods.

Table 95.3: Options for Confidence Intervals

Value of CI=	Method	Additional Options
NONE	No confidence intervals computed
RANK	By inverting rank-score tests
RESAMPLING	By resampling	NREP
SPARSITY	By estimating sparsity function	HS, BF, and IID

By default, when there are fewer than 5,000 observations, fewer than 20 variables in the data set, and the algorithm is simplex, the QUANTREG procedure computes confidence intervals by using the inverted rank-score test method. Otherwise, the resampling method is used.

By default, confidence intervals are not computed for the quantile process, which is estimated when you specify the QUANTILE=PROCESS option in the MODEL statement. Confidence intervals for the quantile process are computed by using the sparsity or resampling methods when you specify CI=SPARSITY or CI=RESAMPLING, respectively. The rank method for confidence intervals is not available for quantile processes because it is computationally prohibitive.

When you specify the SPARSITY option, you have two suboptions for estimating the sparsity function. If you specify the IID suboption, the sparsity function is estimated by assuming that the errors in the linear model are independent and identically distributed (iid). By default, the sparsity function is estimated by assuming that the conditional quantile function is locally linear. For more information, see the section Sparsity. For both methods, two bandwidth selection methods are available: You can specify the BF suboption for the Bofinger method or the HS suboption for the Hall-Sheather method. By default, the Hall-Sheather method is used.

When you specify the RESAMPLING option, you can specify the NREP=n suboption for the number of repetitions. By default, NREP=200. The value of n must be greater than 50.

DATA=SAS-data-set

specifies the input SAS data set to be used by the QUANTREG procedure. By default, the most recently created SAS data set is used.

INEST=SAS-data-set

specifies an input SAS data set that contains initial estimates for all the parameters in the model. The interior point algorithm and the smoothing algorithm use these estimates as a start. For a detailed description of the contents of the INEST= data set, see the section INEST= Data Set.

NAMELEN=n

restricts the length of effect names in tables and output data sets to n characters, where n is a value between 20 and 200. By default, NAMELEN=20.

ORDER=DATA | FORMATTED | FREQ | INTERNAL

specifies the sort order for the levels of the classification variables (which are specified in the CLASS statement).

This option applies to the levels for all classification variables, except when you use the (default) ORDER=FORMATTED option with numeric classification variables that have no explicit format. In that case, the levels of such variables are ordered by their internal value.

The ORDER= option can take the following values:

Value of ORDER=	Levels Sorted By
DATA	Order of appearance in the input data set
FORMATTED	External formatted value, except for numeric variables with no explicit format, which are sorted by their unformatted (internal) value
FREQ	Descending frequency count; levels with the most observations come first in the order
INTERNAL	Unformatted value

By default, ORDER=FORMATTED. For ORDER=FORMATTED and ORDER=INTERNAL, the sort order is machine-dependent.

For more information about sort order, see the chapter on the SORT procedure in the Base SAS Procedures Guide and the discussion of BY-group processing in SAS Language Reference: Concepts.

OUTEST=SAS-data-set

specifies an output SAS data set to contain the parameter estimates for all quantiles. See the section OUTEST= Data Set for a detailed description of the contents of the OUTEST= data set.

PLOT | PLOTS<(global-plot-options)> <=plot-request> PLOT | PLOTS<(global-plot-options)> <=(plot-request < …plot-request > )>

specifies options that control details of the plots. These plots fall into two categories: diagnostic plots and fit plots. You can also use the PLOT= option in the MODEL statement to request the quantile process plot for any effects that are specified in the model. If you do not specify the PLOTS= option, PROC QUANTREG produces the quantile fit plot by default when a single continuous variable is specified in the model.

When you specify only one plot-request, you can omit the parentheses around the plot request.

Here are some examples:

plots=ddplot
plots=(ddplot rdplot)

ODS Graphics must be enabled before plots can be requested. For example:

ods graphics on;

proc quantreg plots=fitplot;
   model y=x1;
run;

For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.

You can specify the following global-plot-options, which apply to all plots that PROC QUANTREG generates:

MAXPOINTS=NONE | number: suppresses plots that have elements that require processing more than number points. The default is MAXPOINTS=5000. This cutoff is ignored if you specify MAXPOINTS=NONE.
ONLY: suppresses the default quantile fit plot. Only plots specifically requested are displayed.

You can specify the following plot-requests:

ALL

creates all appropriate plots.

DDPLOT<(LABEL=ALL | LEVERAGE | NONE | OUTLIER)>

creates a plot of robust distance against Mahalanobis distance. For more information about robust distance, see the section Leverage Point and Outlier Detection. The LABEL= option specifies how the points on this plot are to be labeled, as summarized by Table 95.4.

Table 95.4: Options for Label

Value of LABEL=		Label Method
ALL		Label all points
LEVERAGE		Label leverage points
NONE		No labels
OUTLIERS		Label outliers

By default, the QUANTREG procedure labels both outliers and leverage points.

If you specify ID variables in the ID statement, the values of the first ID variable are used as labels; otherwise, observation numbers are used as labels.

FITPLOT<(NOLIMITS | SHOWLIMITS | NODATA)>

creates a plot of fitted conditional quantiles against the single continuous variable that is specified in the model. This plot is produced only when the response is modeled as a function of a single continuous variable. Multiple lines or curves are drawn on this plot if you specify several quantiles with the QUANTILE= option in the MODEL statement. By default, confidence limits are added to the plot when a single quantile is requested, and the confidence limits are not shown on the plot when multiple quantiles are requested. The NOLIMITS option suppresses the display of the confidence limits. The SHOWLIMITS option adds the confidence limits when multiple quantiles are requested. The NODATA option suppresses the display of the observed data, which are superimposed on the plot by default.

HISTOGRAM

creates a histogram (based on the quantile regression estimates) for the standardized residuals. The histogram is superimposed with a normal density curve and a kernel density curve.

NONE

suppresses all plots.

QQPLOT

creates the normal quantile-quantile plot (based on the quantile regression estimates) for the standardized residuals.

RDPLOT<(LABEL=ALL | LEVERAGE | NONE | OUTLIER)>

creates the plot of standardized residual against robust distance. For more information about robust distance, see the section Leverage Point and Outlier Detection.

The LABEL= option specifies a label method for points on this plot. These label methods are described in Table 95.4.

By default, the QUANTREG procedure labels both outliers and leverage points.

If you specify ID variables in the ID statement, the values of the first ID variable are used as labels; otherwise, observation numbers are used as labels.

PP

requests preprocessing to speed up the interior point algorithm or the smoothing algorithm. The preprocessing uses a subsampling algorithm (which assumes that the data set is evenly distributed) to iteratively reduce the original problem to a smaller one. Preprocessing should be used only for very large data sets, such as data sets with more than 100,000 observations. For more information, see Portnoy and Koenker (1997).