The QUANTREG Procedure
Quantile Regression as an Optimization Problem
The model for linear quantile regression is
![\[ \mb{y} = \bA ^{\prime }\bbeta + \bepsilon \]](images/statug_qreg0058.png)
where  is the
is the 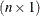 vector of responses,
vector of responses,  is the
is the  regressor matrix,
regressor matrix,  is the
is the  vector of unknown parameters, and
vector of unknown parameters, and  is the
is the 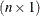 vector of unknown errors.
vector of unknown errors.
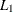 regression, also known as median regression, is a natural extension of the sample median when the response is conditioned
on the covariates. In
regression, also known as median regression, is a natural extension of the sample median when the response is conditioned
on the covariates. In 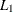 regression, the least absolute residuals estimate
regression, the least absolute residuals estimate  , referred to as the
, referred to as the 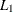 -norm estimate, is obtained as the solution of the following minimization problem:
-norm estimate, is obtained as the solution of the following minimization problem:
![\[ \min _{\bbeta \in \mb{R}^ p} \sum _{i=1}^ n | y_ i - \mb{x}_ i^{\prime }\bbeta | \]](images/statug_qreg0067.png)
More generally, for quantile regression Koenker and Bassett (1978) defined the  regression quantile,
regression quantile, 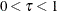 , as any solution to the following minimization problem:
, as any solution to the following minimization problem:
![\[ \min _{\bbeta \in \mb{R}^ p} \left[\sum _{i\in \{ i: y_ i\geq \mb{x}_ i^{\prime }\bbeta \} } \tau |y_ i-\mb{x}_ i^{\prime }\bbeta | + \sum _{i\in \{ i: y_ i< \mb{x}_ i^{\prime }\bbeta \} } (1-\tau ) |y_ i-\mb{x}_ i^{\prime }\bbeta |\right] \]](images/statug_qreg0068.png)
The solution is denoted as  , and the
, and the  -norm estimate corresponds to
-norm estimate corresponds to  . The
. The  regression quantile is an extension of the
regression quantile is an extension of the  sample quantile
sample quantile  , which can be formulated as the solution of
, which can be formulated as the solution of
![\[ \min _{\xi \in \mb{R}} \left[ \sum _{i\in \{ i: y_ i\geq \xi \} } \tau |y_ i-\xi | + \sum _{i\in \{ i: y_ i< \xi \} } (1-\tau ) |y_ i-\xi | \right] \]](images/statug_qreg0072.png)
If you specify weights  , with the WEIGHT statement, weighted quantile regression is carried out by solving
, with the WEIGHT statement, weighted quantile regression is carried out by solving
![\[ \min _{\bbeta _ w \in \mb{R}^ p} \left[\sum _{i\in \{ i: y_ i\geq \mb{x}_ i^{\prime }\bbeta _ w\} } w_ i \tau |y_ i-\mb{x}_ i^{\prime }\bbeta _ w| + \sum _{i\in \{ i: y_ i< \mb{x}_ i^{\prime }\bbeta _ w\} } w_ i (1-\tau ) |y_ i-\mb{x}_ i^{\prime }\bbeta _ w|\right] \]](images/statug_qreg0074.png)
Weighted regression quantiles  can be used for L-estimation (Koenker and Zhao 1994).
can be used for L-estimation (Koenker and Zhao 1994).
