The QUANTREG Procedure

Quantile Regression

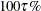Quantile regression generalizes the concept of a univariate quantile to a conditional quantile given one or more covariates. Recall that a student’s score on a test is at the $\tau $ quantile if his or her score is better than that of $100\tau \% $ of the students who took the test. The score is also said to be at the 100$\tau $th percentile.

For a random variable Y with probability distribution function

\[ F(y) = \mbox{ Prob } (Y\leq y) \]

the $\tau $ quantile of Y is defined as the inverse function

\[ Q(\tau ) = \mbox{ inf }\{ y: F(y)\geq \tau \} \]

where the quantile level $\tau $ ranges between 0 and 1. In particular, the median is $Q(1/2)$.

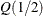For a random sample 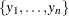$\{ y_1,\ldots ,y_ n\} $ of Y, it is well known that the sample median minimizes the sum of absolute deviations:

\[ \mbox{median} = {\arg \min }_{\xi \in \mb{R}} \sum _{i=1}^ n |y_ i-\xi | \]

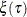Likewise, the general $\tau $ sample quantile $\xi (\tau )$, which is the analog of 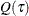$Q(\tau )$, is formulated as the minimizer

\[ \xi (\tau ) = {\arg \min }_{\xi \in \mb{R}} \sum _{i=1}^ n \rho _\tau (y_ i-\xi ) \]

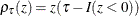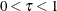where $\rho _{\tau }(z) = z(\tau -I(z<0))$, $0<\tau <1$, and where 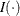$I(\cdot )$ denotes the indicator function. The loss function 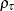$\rho _\tau $ assigns a weight of $\tau $ to positive residuals 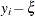$y_ i - \xi $ and a weight of 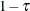$1-\tau $ to negative residuals.

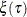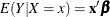Using this loss function, the linear conditional quantile function extends the $\tau $ sample quantile $\xi (\tau )$ to the regression setting in the same way that the linear conditional mean function extends the sample mean. Recall that OLS regression estimates the linear conditional mean function $E(Y|X=x) = \mb{x}^{\prime }\bbeta $ by solving for

\[ \hat\bbeta = {\arg \min }_{\bbeta \in \mb{R}^ p} \sum _{i=1}^ n(y_ i-\mb{x}_ i^{\prime }\bbeta )^2 \]

The estimated parameter 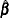$\hat\bbeta $ minimizes the sum of squared residuals in the same way that the sample mean 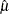$\hat\mu $ minimizes the sum of squares:

\[ \hat\mu = {\arg \min }_{\mu \in \mb{R}} \sum _{i=1}^ n(y_ i-\mu )^2 \]

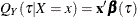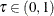Likewise, quantile regression estimates the linear conditional quantile function, $Q_ Y(\tau |X=x) = \mb{x}^{\prime }\bbeta (\tau )$, by solving the following equation for $\tau \in (0, 1)$:

\[ \hat\bbeta (\tau ) = {\arg \min }_{\bbeta \in \mb{R}^ p} \sum _{i=1}^ n\rho _\tau (y_ i- \mb{x}_ i^{\prime } \bbeta ) \]

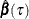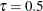The quantity $\hat\bbeta (\tau )$ is called the $\tau $ regression quantile. The case $\tau =0.5$ (which minimizes the sum of absolute residuals) corresponds to median regression (which is also known as 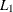$L_1$ regression).

The following set of regression quantiles is referred to as the quantile process:

\[ \{ \bbeta (\tau ): \tau \in (0, 1) \} \]

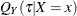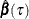The QUANTREG procedure computes the quantile function $Q_ Y(\tau |X=x)$ and conducts statistical inference on the estimated parameters $\hat\bbeta (\tau )$.