The QUANTREG Procedure
Confidence Interval
The QUANTREG procedure provides three methods to compute confidence intervals for the regression quantile parameter 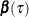 : sparsity, rank, and resampling. The sparsity method is the most direct and the fastest, but it involves estimation of the
sparsity function, which is not robust for data that are not independently and identically distributed. To deal with this
problem, the QUANTREG procedure uses a local estimate of the sparsity function to compute a Huber sandwich estimate. The rank
method, which computes confidence intervals by inverting the rank score test, does not suffer from this problem. However,
the rank method uses the simplex algorithm and is computationally expensive with large data sets. The resampling method, which
uses the bootstrap approach, addresses these problems, but at a computation cost.
: sparsity, rank, and resampling. The sparsity method is the most direct and the fastest, but it involves estimation of the
sparsity function, which is not robust for data that are not independently and identically distributed. To deal with this
problem, the QUANTREG procedure uses a local estimate of the sparsity function to compute a Huber sandwich estimate. The rank
method, which computes confidence intervals by inverting the rank score test, does not suffer from this problem. However,
the rank method uses the simplex algorithm and is computationally expensive with large data sets. The resampling method, which
uses the bootstrap approach, addresses these problems, but at a computation cost.
Based on these properties, the QUANTREG uses a combination of the resampling and rank methods as the default. For data sets that have more than either 5,000 observations or more than 20 variables, the QUANTREG procedure uses the MCMB resampling method; otherwise it uses the rank method. You can request a particular method by using the CI= option in the PROC QUANTREG statement.
Sparsity
Consider the linear model
![\[ y_ i = \mb{x}_ i^{\prime }\bbeta + \epsilon _ i \]](images/statug_qreg0209.png)
Assume that 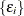 ,
, 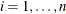 , are iid with a distribution F and a density
, are iid with a distribution F and a density 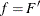 , where
, where 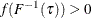 in a neighborhood of
in a neighborhood of  . Under some mild conditions,
. Under some mild conditions,
![\[ \sqrt {n}({\hat\bbeta }(\tau ) - \bbeta (\tau )) \rightarrow N(0, \omega ^2(\tau , F) \bOmega ^{-1}) \]](images/statug_qreg0214.png)
where 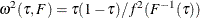 and
and 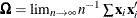 (Koenker and Bassett 1982b).
(Koenker and Bassett 1982b).
This asymptotic distribution for the regression quantile 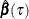 can be used to construct confidence intervals. However, the reciprocal of the density function,
can be used to construct confidence intervals. However, the reciprocal of the density function,
![\[ s(\tau ) = [f(F^{-1}(\tau ))]^{-1} \]](images/statug_qreg0218.png)
which is called the sparsity function, must first be estimated.
Because
![\[ s(t) = {\frac d{dt}} F^{-1}(t) \]](images/statug_qreg0219.png)
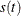 can be estimated by the difference quotient of the empirical quantile function—that is,
can be estimated by the difference quotient of the empirical quantile function—that is,
![\[ {\hat s}_ n(t) = [{\hat F}_ n^{-1}(t+h_ n) - {\hat F}_ n^{-1}(t-h_ n)] \slash 2h_ n \]](images/statug_qreg0221.png)
where 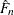 is an estimate of
is an estimate of 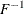 and
and 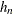 is a bandwidth that tends to 0 as
is a bandwidth that tends to 0 as 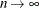 .
.
The QUANTREG procedure provides two bandwidth methods. The Bofinger bandwidth
![\[ h_ n = n^{-1\slash 5} ( {\frac{4.5s^2(t)}{(s^{(2)}(t))^2}} )^{1\slash 5} \]](images/statug_qreg0226.png)
is an optimizer of mean squared error for standard density estimation. The Hall-Sheather bandwidth
![\[ h_ n = n^{-1\slash 3} z_\alpha ^{2\slash 3} ({\frac{1.5 s(t)}{s^{(2)}(t)}} )^{1\slash 3} \]](images/statug_qreg0227.png)
is based on Edgeworth expansions for studentized quantiles, where 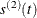 is the second derivative of
is the second derivative of 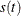 and
and 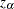 satisfies
satisfies 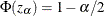 for the construction of
for the construction of 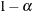 confidence intervals. The following quantity is not sensitive to f and can be estimated by assuming f is Gaussian:
confidence intervals. The following quantity is not sensitive to f and can be estimated by assuming f is Gaussian:
![\[ {\frac{s(t)}{s^{(2)}(t)}} = {\frac{f^2}{2(f^{(1)} \slash f)^2 + [(f^{(1)} \slash f)^2 - f^{(2)}\slash f ] }} \]](images/statug_qreg0231.png)
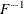 can be estimated in either of the following ways:
can be estimated in either of the following ways:
-
by the empirical quantile function of the residuals from the quantile regression fit,
![\[ {\hat F}^{-1}(t) = r_{(i)},\ {\mbox{ for }} t\in [(i-1)\slash n, i\slash n), \]](images/statug_qreg0233.png)
-
by the empirical quantile function of regression proposed by Bassett and Koenker (1982),
![\[ {\hat F}^{-1}(t) = {\bar{\mb{x}}}^{\prime } {\hat\bbeta }(t) \]](images/statug_qreg0234.png)
The QUANTREG procedure interpolates the first empirical quantile function and produces the piecewise linear version:
![\[ {\hat F}^{-1}(t) = \left\{ \begin{array}{ll} r_{(1)} & {\mbox{if }} t\in [0, 1\slash 2n) \\ \lambda r_{(i+1)} + (1-\lambda ) r_{(i)} & {\mbox{if }} t\in [(2i-1)\slash 2n, (2i+1)\slash 2n) \\ r_{(n)} & {\mbox{if }} t\in [(2n-1), 1] \\ \end{array} \right. \]](images/statug_qreg0235.png)
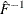 is set to a constant if
is set to a constant if 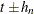 falls outside
falls outside ![$[0,1]$](images/statug_qreg0238.png) .
.
This estimator of the sparsity function is sensitive to the iid assumption. Alternately, Koenker and Machado (1999) consider the non-iid case. By assuming local linearity of the conditional quantile function 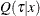 in x, they propose a local estimator of the density function by using the difference quotient. A Huber sandwich estimate of the
covariance and standard error is computed and used to construct the confidence intervals. One difficulty with this method
is the selection of the bandwidth when using the difference quotient. With a small sample size, either the Bofinger or the
Hall-Sheather bandwidth tends to be too large to assure local linearity of the conditional quantile function. The QUANTREG
procedure uses a heuristic bandwidth selection in these cases.
in x, they propose a local estimator of the density function by using the difference quotient. A Huber sandwich estimate of the
covariance and standard error is computed and used to construct the confidence intervals. One difficulty with this method
is the selection of the bandwidth when using the difference quotient. With a small sample size, either the Bofinger or the
Hall-Sheather bandwidth tends to be too large to assure local linearity of the conditional quantile function. The QUANTREG
procedure uses a heuristic bandwidth selection in these cases.
By default, the QUANTREG procedure computes non-iid confidence intervals. You can request iid confidence intervals by specifying the IID option in the PROC QUANTREG statement.
Inversion of Rank Tests
The classical theory of rank tests can be extended to test the hypothesis 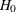 :
: 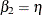 in the linear regression model
in the linear regression model 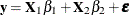 . Here,
. Here, 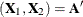 . See Gutenbrunner and Jureckova (1992) for more details. By inverting this test, confidence intervals can be computed for the regression quantiles that correspond
to
. See Gutenbrunner and Jureckova (1992) for more details. By inverting this test, confidence intervals can be computed for the regression quantiles that correspond
to 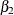 .
.
The rank score function 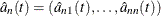 can be obtained by solving the dual problem:
can be obtained by solving the dual problem:
![\[ \max _ a \{ (\mb{y}-\bX _2\bm {\eta })^{\prime }a | \bX _1^{\prime }a = (1-t)\bX _1^{\prime }\mb{e}, \ a\in [0,1]^ n \} \]](images/statug_qreg0246.png)
For a fixed quantile  , integrating
, integrating 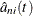 with respect to the
with respect to the  -quantile score function
-quantile score function
![\[ \varphi _\tau (t) = \tau - I(t<\tau ) \]](images/statug_qreg0248.png)
yields the  -quantile scores
-quantile scores
![\[ {\hat b}_{ni} = -\int _0^1 \varphi _\tau (t) d {\hat a}_{ni}(t) = {\hat a}_{ni}(\tau ) -(1-\tau ) \]](images/statug_qreg0249.png)
Under the null hypothesis 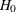 :
: 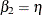 ,
,
![\[ S_ n(\eta ) = n^{-1\slash 2} \bX _2^{\prime }{\hat b}_ n(\eta ) \rightarrow N(0,\tau (1-\tau ) \bOmega _ n) \]](images/statug_qreg0250.png)
for large n, where 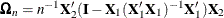 .
.
Let
![\[ T_ n(\eta ) = {\frac1{\sqrt {\tau (1-\tau )}}} S_ n(\eta ) \bOmega _ n^{-1\slash 2} \]](images/statug_qreg0252.png)
Then 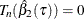 from the constraint
from the constraint 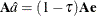 in the full model. In order to obtain confidence intervals for
in the full model. In order to obtain confidence intervals for 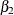 , a critical value can be specified for
, a critical value can be specified for 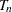 . The dual vector
. The dual vector 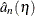 is a piecewise constant in
is a piecewise constant in 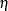 , and
, and 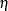 can be altered without compromising the optimality of
can be altered without compromising the optimality of 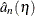 as long as the signs of the residuals in the primal quantile regression problem do not change. When
as long as the signs of the residuals in the primal quantile regression problem do not change. When 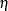 gets to such a boundary, the solution does change. But it can be restored by taking one simplex pivot. The process can continue
in this way until
gets to such a boundary, the solution does change. But it can be restored by taking one simplex pivot. The process can continue
in this way until 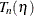 exceeds the specified critical value. Because
exceeds the specified critical value. Because 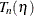 is piecewise constant, interpolation can be used to obtain the desired level of confidence interval (Koenker and d’Orey 1994).
is piecewise constant, interpolation can be used to obtain the desired level of confidence interval (Koenker and d’Orey 1994).
Resampling
The bootstrap can be implemented to compute confidence intervals for regression quantile estimates. As in other regression applications, both the residual bootstrap and the xy-pair bootstrap can be used. The former assumes iid random errors and resamples from the residuals, whereas the latter resamples xy pairs and accommodates some forms of heteroscedasticity. Koenker (1994) considered a more interesting resampling mechanism, resampling directly from the full regression quantile process, which he called the Heqf bootstrap.
In contrast with these bootstrap methods, Parzen, Wei, and Ying (1994) observed that the following estimating equation for the  regression quantile is a pivotal quantity for the
regression quantile is a pivotal quantity for the  quantile regression parameter
quantile regression parameter 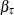 :
:
![\[ S(\bbeta ) = n^{-1\slash 2} \sum _{i=1}^ n \mb{x}_ i(\tau -I(y_ i\leq \mb{x}_ i^{\prime }\bbeta )) \]](images/statug_qreg0260.png)
In other words, the distribution of 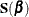 can be generated exactly by a random vector
can be generated exactly by a random vector 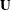 , which is a weighted sum of independent, re-centered Bernoulli variables. They further showed that for large n, the distribution of
, which is a weighted sum of independent, re-centered Bernoulli variables. They further showed that for large n, the distribution of 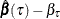 can be approximated by the conditional distribution of
can be approximated by the conditional distribution of 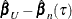 , where
, where 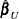 solves an augmented quantile regression problem by using n + 1 observations that have
solves an augmented quantile regression problem by using n + 1 observations that have 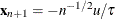 and
and 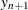 sufficiently large for a given realization of u. By exploiting the asymptotically pivotal role of the quantile regression "gradient condition," this approach also achieves
some robustness to certain heteroscedasticity.
sufficiently large for a given realization of u. By exploiting the asymptotically pivotal role of the quantile regression "gradient condition," this approach also achieves
some robustness to certain heteroscedasticity.
Although the bootstrap method by Parzen, Wei, and Ying (1994) is much simpler, it is too time-consuming for relatively large data sets, especially for high-dimensional data sets. The QUANTREG procedure implements a new, general resampling method developed by He and Hu (2002), which is called the Markov chain marginal bootstrap (MCMB). For quantile regression, the MCMB method has the advantage that it solves p one-dimensional equations instead of solving p-dimensional equations, as the previous bootstrap methods do. This greatly improves the feasibility of the resampling method in computing confidence intervals for regression quantiles.
