The POWER Procedure
- Overview
-
Getting Started

-
Syntax
 PROC POWER StatementCOXREG StatementLOGISTIC StatementMULTREG StatementONECORR StatementONESAMPLEFREQ StatementONESAMPLEMEANS StatementONEWAYANOVA StatementPAIREDFREQ StatementPAIREDMEANS StatementPLOT StatementTWOSAMPLEFREQ StatementTWOSAMPLEMEANS StatementTWOSAMPLESURVIVAL StatementTWOSAMPLEWILCOXON Statement
PROC POWER StatementCOXREG StatementLOGISTIC StatementMULTREG StatementONECORR StatementONESAMPLEFREQ StatementONESAMPLEMEANS StatementONEWAYANOVA StatementPAIREDFREQ StatementPAIREDMEANS StatementPLOT StatementTWOSAMPLEFREQ StatementTWOSAMPLEMEANS StatementTWOSAMPLESURVIVAL StatementTWOSAMPLEWILCOXON Statement -
Details

-
Examples
 One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test
One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test - References
LOGISTIC Statement
-
LOGISTIC <options>;
The LOGISTIC statement performs power and sample size analyses for the likelihood ratio chi-square test of a single predictor in binary logistic regression, possibly in the presence of one or more covariates that might be correlated with the tested predictor.
Summary of Options
Table 89.4 summarizes the options available in the LOGISTIC statement.
Table 89.4: LOGISTIC Statement Options
|
Option |
Description |
|---|---|
|
Define analysis |
|
|
Specifies the statistical analysis |
|
|
Specify analysis information |
|
|
Specifies the significance level |
|
|
Specifies the distributions of predictor variables |
|
|
Specifies the distribution of the predictor variable being tested |
|
|
Defines a distribution for a predictor variable |
|
|
Specify effects |
|
|
Specifies the multiple correlation between the predictor and the covariates |
|
|
Specifies the odds ratios for the covariates |
|
|
Specifies the regression coefficients for the covariates |
|
|
Specifies the default change in the predictor variables |
|
|
Specifies the intercept |
|
|
Specifies the response probability |
|
|
Specifies the odds ratio being tested |
|
|
Specifies the regression coefficient for the predictor variable |
|
|
Specifies the changes in the predictor variables |
|
|
Specify sample size |
|
|
Enables fractional input and output for sample sizes |
|
|
Specifies the sample size |
|
|
Specify power |
|
|
Specifies the desired power of the test |
|
|
Specify computational method |
|
|
Specifies the default number of categories for each predictor variable |
|
|
Specifies the number of categories for predictor variables |
|
|
Control ordering in output |
|
|
Controls the output order of parameters |
|
Table 89.5 summarizes the valid result parameters in the LOGISTIC statement.
Table 89.5: Summary of Result Parameters in the LOGISTIC Statement
Dictionary of Options
Restrictions on Option Combinations
To specify the intercept in the full model, choose one of the following two parameterizations:
-
intercept (using the INTERCEPT= options)
-
Prob(Y = 1) when all predictors are equal to their means (using the RESPONSEPROB= option)
To specify the effect associated with the predictor variable being tested, choose one of the following two parameterizations:
-
odds ratio (using the TESTODDSRATIO= options)
-
regression coefficient (using the TESTREGCOEFFS= option)
To describe the effects of the covariates in the full model, choose one of the following two parameterizations:
-
odds ratios (using the COVODDSRATIOS= options)
-
regression coefficients (using the COVREGCOEFFS= options)
Option Groups for Common Analyses
This section summarizes the syntax for the common analyses that are supported in the LOGISTIC statement.
Likelihood Ratio Chi-Square Test for One Predictor
You can express effects in terms of response probability and odds ratios, as in the following statements:
proc power;
logistic
vardist("x1a") = normal(0, 2)
vardist("x1b") = normal(0, 3)
vardist("x2") = poisson(7)
vardist("x3a") = ordinal((-5 0 5) : (.3 .4 .3))
vardist("x3b") = ordinal((-5 0 5) : (.4 .3 .3))
testpredictor = "x1a" "x1b"
covariates = "x2" | "x3a" "x3b"
responseprob = 0.15
testoddsratio = 1.75
covoddsratios = (2.1 1.4)
ntotal = 100
power = .;
run;
The VARDIST= options define the distributions of the predictor variables. The TESTPREDICTOR= option specifies two scenarios for the test predictor distribution, Normal(10,2) and Normal(10,3). The COVARIATES= option specifies two covariates, the first with a Poisson(7) distribution. The second covariate has an ordinal distribution on the values –5, 0, and 5 with two scenarios for the associated probabilities: (.3, .4, .3) and (.4, .3, .3). The response probability in the full model with all variables equal to zero is specified by the RESPONSEPROB= option as 0.15. The odds ratio for a unit decrease in the tested predictor is specified by the TESTODDSRATIO= option to be 1.75. Corresponding odds ratios for the two covariates in the full model are specified by the COVODDSRATIOS= option to be 2.1 and 1.4. The POWER= . option requests a solution for the power at a sample size of 100 as specified by the NTOTAL= option.
Default values of the TEST= and ALPHA= options specify a likelihood ratio test of the first predictor with a significance level of 0.05. The default of DEFAULTUNIT= 1 specifies that all odds ratios are defined in terms of unit changes in predictors. The default of DEFAULTNBINS= 10 specifies that each of the three predictor variables is discretized into a distribution with 10 categories in internal calculations.
You can also express effects in terms of regression coefficients, as in the following statements:
proc power;
logistic
vardist("x1a") = normal(0, 2)
vardist("x1b") = normal(0, 3)
vardist("x2") = poisson(7)
vardist("x3a") = ordinal((-5 0 5) : (.3 .4 .3))
vardist("x3b") = ordinal((-5 0 5) : (.4 .3 .3))
testpredictor = "x1a" "x1b"
covariates = "x2" | "x3a" "x3b"
intercept = -6.928162
testregcoeff = 0.5596158
covregcoeffs = (0.7419373 0.3364722)
ntotal = 100
power = .;
run;
The regression coefficients for the tested predictor (TESTREGCOEFF= 0.5596158) and covariates (COVREGCOEFFS= (0.7419373 0.3364722)) are determined by taking the logarithm of the corresponding odds ratios. The intercept in the full model is specified as –6.928162 by the INTERCEPT= option. This number is calculated according to the formula at the end of Analyses in the LOGISTIC Statement, which expresses the intercept in terms of the response probability, regression coefficients, and predictor means:
![\[ \mbox{Intercept} = \log \left(\frac{0.15}{1-0.15}\right) - \left(0.5596158(0) + 0.7419373(7) + 0.3364722(0) \right) \]](images/statug_power0024.png)

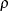





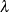

![$]$](images/statug_power0022.png)