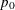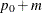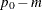The POWER Procedure

ONESAMPLEFREQ Statement

Subsections:

  • ONESAMPLEFREQ <options>;

The ONESAMPLEFREQ statement performs power and sample size analyses for exact and approximate tests (including equivalence, noninferiority, and superiority) and confidence interval precision for a single binomial proportion.

Summary of Options

Table 89.10 summarizes the options available in the ONESAMPLEFREQ statement.

Table 89.10: ONESAMPLEFREQ Statement Options

Option

Description

Define analysis

CI=

Specifies an analysis of precision of a confidence interval

TEST=

Specifies the statistical analysis

Specify analysis information

ALPHA=

Specifies the significance level

EQUIVBOUNDS=

Specifies the lower and upper equivalence bounds

LOWER=

Specifies the lower equivalence bound

MARGIN=

Specifies the equivalence or noninferiority or superiority margin

NULLPROPORTION=

Specifies the null proportion

SIDES=

Specifies the number of sides and the direction of the statistical test

UPPER=

Specifies the upper equivalence bound

Specify effect

HALFWIDTH=

Specifies the desired confidence interval half-width

PROPORTION=

Specifies the binomial proportion

Specify variance estimation

VAREST=

Specifies how the variance is computed

Specify sample size

NFRACTIONAL

Enables fractional input and output for sample sizes

NTOTAL=

Specifies the sample size

Specify power and related probabilities

POWER=

Specifies the desired power of the test

PROBWIDTH=

Specifies the probability of obtaining a confidence interval half-width less than or equal to the value specified by HALFWIDTH=

Choose computational method

METHOD=

Specifies the computational method

Control ordering in output

OUTPUTORDER=

Controls the output order of parameters


Table 89.11 summarizes the valid result parameters for different analyses in the ONESAMPLEFREQ statement.

Table 89.11: Summary of Result Parameters in the ONESAMPLEFREQ Statement

Analyses

Solve For

Syntax

CI= WILSON

Prob(width)

PROBWIDTH= .

CI= AGRESTICOULL

Prob(width)

PROBWIDTH= .

CI= JEFFREYS

Prob(width)

PROBWIDTH= .

CI= EXACT

Prob(width)

PROBWIDTH= .

CI= WALD

Prob(width)

PROBWIDTH= .

CI= WALD_CORRECT

Prob(width)

PROBWIDTH= .

TEST= ADJZ METHOD= EXACT

Power

POWER= .

TEST= ADJZ METHOD= NORMAL

Power

POWER= .

 

Sample size

NTOTAL= .

TEST= EQUIV_ADJZ METHOD= EXACT

Power

POWER= .

TEST= EQUIV_ADJZ METHOD= NORMAL

Power

POWER= .

 

Sample size

NTOTAL= .

TEST= EQUIV_EXACT

Power

POWER= .

TEST= EQUIV_Z METHOD= EXACT

Power

POWER= .

TEST= EQUIV_Z METHOD= NORMAL

Power

POWER= .

 

Sample size

NTOTAL= .

TEST= EXACT

Power

POWER= .

TEST= Z METHOD= EXACT

Power

POWER= .

TEST= Z METHOD= NORMAL

Power

POWER= .

 

Sample size

NTOTAL= .


Dictionary of Options

ALPHA=number-list

specifies the level of significance of the statistical test. The default is 0.05, which corresponds to the usual 0.05 $\times $ 100% = 5% level of significance. If the CI= and SIDES= 1 options are used, then the value must be less than 0.5. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

CI
CI=AGRESTICOULL | AC
CI=JEFFREYS
CI=EXACT | CLOPPERPEARSON | CP
CI=WALD
CI=WALD_CORRECT
CI=WILSON | SCORE

specifies an analysis of precision of a confidence interval for the sample binomial proportion.

The value of the CI= option specifies the type of confidence interval. The CI= AGRESTICOULL option is a generalization of the "Adjusted Wald / add 2 successes and 2 failures" interval of Agresti and Coull (1998) and is presented in Brown, Cai, and DasGupta (2001). It corresponds to the TABLES / BINOMIAL (AGRESTICOULL) option in PROC FREQ. The CI= JEFFREYS option specifies the equal-tailed Jeffreys prior Bayesian interval, which corresponds to the TABLES / BINOMIAL (JEFFREYS) option in PROC FREQ. The CI= EXACT option specifies the exact Clopper-Pearson confidence interval based on enumeration, which corresponds to the TABLES / BINOMIAL (EXACT) option in PROC FREQ. The CI= WALD option specifies the confidence interval based on the Wald test (also commonly called the z test or normal-approximation test), which corresponds to the TABLES / BINOMIAL (WALD) option in PROC FREQ. The CI= WALD_CORRECT option specifies the confidence interval based on the Wald test with continuity correction, which corresponds to the TABLES / BINOMIAL (CORRECT WALD) option in PROC FREQ. The CI= WILSON option (the default) specifies the confidence interval based on the score statistic, which corresponds to the TABLES / BINOMIAL (WILSON) option in PROC FREQ.

Instead of power, the relevant probability for this analysis is the probability of achieving a desired precision. Specifically, it is the probability that the half-width of the confidence interval will be at most the value specified by the HALFWIDTH= option.

EQUIVBOUNDS=grouped-number-list

specifies the lower and upper equivalence bounds, representing the same information as the combination of the LOWER= and UPPER= options but grouping them together. The EQUIVBOUNDS= option can be used only with equivalence analyses (TEST= EQUIV_ADJZ | EQUIV_EXACT | EQUIV_Z). Values must be strictly between 0 and 1. For information about specifying the grouped-number-list, see the section Specifying Value Lists in Analysis Statements.

HALFWIDTH=number-list

specifies the desired confidence interval half-width. The half-width for a two-sided interval is the length of the confidence interval divided by two. This option can be used only with the CI= analysis. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

LOWER=number-list

specifies the lower equivalence bound for the binomial proportion. The LOWER= option can be used only with equivalence analyses (TEST= EQUIV_ADJZ | EQUIV_EXACT | EQUIV_Z). Values must be strictly between 0 and 1. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

MARGIN=number-list

specifies the equivalence or noninferiority or superiority margin, depending on the analysis.

The MARGIN= option can be used with one-sided analyses (SIDES = 1 | U | L), in which case it specifies the margin added to the null proportion value in the hypothesis test, resulting in a noninferiority or superiority test (depending on the agreement between the effect and hypothesis directions and the sign of the margin). A test with a null proportion $p_0$ and a margin m is the same as a test with null proportion $p_0 + m$ and no margin.

The MARGIN= option can also be used with equivalence analyses (TEST= EQUIV_ADJZ | EQUIV_EXACT | EQUIV_Z) when the NULLPROPORTION= option is used, in which case it specifies the lower and upper equivalence bounds as $p_0 - m$ and $p_0 + m$, where $p_0$ is the value of the NULLPROPORTION= option and m is the value of the MARGIN= option.

The MARGIN= option cannot be used in conjunction with the SIDES= 2 option. (Instead, specify an equivalence analysis by using TEST= EQUIV_ADJZ or TEST= EQUIV_EXACT or TEST= EQUIV_Z). Also, the MARGIN= option cannot be used with the CI= option.

Values must be strictly between –1 and 1. In addition, the sum of NULLPROPORTION and MARGIN must be strictly between 0 and 1 for one-sided analyses, and the derived lower equivalence bound (2 * NULLPROPORTION – MARGIN) must be strictly between 0 and 1 for equivalence analyses.

For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

METHOD=EXACT | NORMAL

specifies the computational method. METHOD= EXACT (the default) computes exact results by using the binomial distribution. METHOD= NORMAL computes approximate results by using the normal approximation to the binomial distribution.

NFRACTIONAL
NFRAC

enables fractional input and output for sample sizes. This option is invalid when the METHOD= EXACT option is specified. See the section Sample Size Adjustment Options for information about the ramifications of the presence (and absence) of the NFRACTIONAL option.

NTOTAL=number-list

specifies the sample size or requests a solution for the sample size by specifying a missing value (NTOTAL= .). For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

NULLPROPORTION=number-list
NULLP=number-list

specifies the null proportion. A value of 0.5 corresponds to the sign test. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

OUTPUTORDER=INTERNAL | REVERSE | SYNTAX

controls how the input and default analysis parameters are ordered in the output. OUTPUTORDER= INTERNAL (the default) arranges the parameters in the output according to the following order of their corresponding options:

The OUTPUTORDER= SYNTAX option arranges the parameters in the output in the same order in which their corresponding options are specified in the ONESAMPLEFREQ statement. The OUTPUTORDER= REVERSE option arranges the parameters in the output in the reverse of the order in which their corresponding options are specified in the ONESAMPLEFREQ statement.

POWER=number-list

specifies the desired power of the test or requests a solution for the power by specifying a missing value (POWER= .). The power is expressed as a probability, a number between 0 and 1, rather than as a percentage. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

PROBWIDTH=number-list

specifies the desired probability of obtaining a confidence interval half-width less than or equal to the value specified by the HALFWIDTH= option. A missing value (PROBWIDTH= .) requests a solution for this probability. Values are expressed as probabilities (for example, 0.9) rather than percentages. This option can be used only with the CI= analysis. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

PROPORTION=number-list
P=number-list

specifies the binomial proportion—that is, the expected proportion of successes in the hypothetical binomial trial. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

SIDES=keyword-list

specifies the number of sides (or tails) and the direction of the statistical test. For information about specifying the keyword-list, see the section Specifying Value Lists in Analysis Statements. You can specify the following keywords:

1

specifies a one-sided test, with the alternative hypothesis in the same direction as the effect.

2

specifies a two-sided test.

U

specifies an upper one-sided test, with the alternative hypothesis indicating a proportion greater than the null value.

L

specifies a lower one-sided test, with the alternative hypothesis indicating a proportion less than the null value.

If the effect size is zero, then SIDES= 1 is not permitted; instead, specify the direction of the test explicitly in this case with either SIDES= L or SIDES= U. By default, SIDES=2.

TEST= ADJZ | EQUIV_ADJZ | EQUIV_EXACT | EQUIV_Z | EXACT | Z
TEST

specifies the statistical analysis. TEST= ADJZ specifies a normal-approximate z test with continuity adjustment. TEST= EQUIV_ADJZ specifies a normal-approximate two-sided equivalence test based on the z statistic with continuity adjustment and a TOST (two one-sided tests) procedure. TEST= EQUIV_EXACT specifies the exact binomial two-sided equivalence test based on a TOST (two one-sided tests) procedure. TEST= EQUIV_Z specifies a normal-approximate two-sided equivalence test based on the z statistic without any continuity adjustment, which is the same as the chi-square statistic, and a TOST (two one-sided tests) procedure. TEST or TEST= EXACT (the default) specifies the exact binomial test. TEST= Z specifies a normal-approximate z test without any continuity adjustment, which is the same as the chi-square test when SIDES= 2.

UPPER=number-list

specifies the upper equivalence bound for the binomial proportion. The UPPER= option can be used only with equivalence analyses (TEST= EQUIV_ADJZ | EQUIV_EXACT | EQUIV_Z). Values must be strictly between 0 and 1. For information about specifying the number-list, see the section Specifying Value Lists in Analysis Statements.

VAREST=keyword-list

specifies how the variance is computed in the test statistic for the TEST= Z, TEST= ADJZ, TEST= EQUIV_Z, and TEST= EQUIV_ADJZ analyses. For information about specifying the keyword-list, see the section Specifying Value Lists in Analysis Statements. Valid keywords are as follows:

NULL

(the default) estimates the variance by using the null proportion(s) (specified by some combination of the NULLPROPORTION= , MARGIN= , LOWER= , and UPPER= options). For TEST= Z and TEST= ADJZ, the null proportion is the value of the NULLPROPORTION= option plus the value of the MARGIN= option (if it is used). For TEST= EQUIV_Z and TEST= EQUIV_ADJZ, there are two null proportions, which correspond to the lower and upper equivalence bounds, one for each test in the TOST (two one-sided tests) procedure.

SAMPLE

estimates the variance by using the observed sample proportion.

This option is ignored if the analysis is one other than TEST= Z, TEST= ADJZ, TEST= EQUIV_Z, or TEST= EQUIV_ADJZ.

Option Groups for Common Analyses

This section summarizes the syntax for the common analyses that are supported in the ONESAMPLEFREQ statement.

Exact Test of a Binomial Proportion

The following statements demonstrate a power computation for the exact test of a binomial proportion. Defaults for the SIDES= and ALPHA= options specify a two-sided test with a 0.05 significance level. 

proc power;
   onesamplefreq test=exact
      nullproportion = 0.2
      proportion = 0.3
      ntotal = 100
      power = .;
run;
z Test

The following statements demonstrate a sample size computation for the z test of a binomial proportion. Defaults for the SIDES= , ALPHA= , and VAREST= options specify a two-sided test with a 0.05 significance level that uses the null variance estimate. 

proc power;
   onesamplefreq test=z method=normal
      nullproportion = 0.8
      proportion = 0.85
      sides = u
      ntotal = .
      power = .9;
run;
z Test with Continuity Adjustment

The following statements demonstrate a sample size computation for the z test of a binomial proportion with a continuity adjustment. Defaults for the SIDES= , ALPHA= , and VAREST= options specify a two-sided test with a 0.05 significance level that uses the null variance estimate. 

proc power;
   onesamplefreq test=adjz method=normal
      nullproportion = 0.15
      proportion = 0.1
      sides = l
      ntotal = .
      power = .9;
run;
Exact Equivalence Test for a Binomial Proportion

You can specify equivalence bounds by using the EQUIVBOUNDS= option, as in the following statements: 

proc power;
   onesamplefreq test=equiv_exact
      proportion = 0.35
      equivbounds = (0.2 0.4)
      ntotal = 50
      power = .;
run;

You can also specify the combination of NULLPROPORTION= and MARGIN= options: 

proc power;
   onesamplefreq test=equiv_exact
      proportion = 0.35
      nullproportion = 0.3
      margin = 0.1
      ntotal = 50
      power = .;
run;

Finally, you can specify the combination of LOWER= and UPPER= options: 

proc power;
   onesamplefreq test=equiv_exact
      proportion = 0.35
      lower = 0.2
      upper = 0.4
      ntotal = 50
      power = .;
run;

Note that the three preceding analyses are identical.

Exact Noninferiority Test for a Binomial Proportion

A noninferiority test corresponds to an upper one-sided test with a negative-valued margin, as demonstrated in the following statements: 

proc power;
   onesamplefreq test=exact
      sides = U
      proportion = 0.15
      nullproportion = 0.1
      margin = -0.02
      ntotal = 130
      power = .;
run;
Exact Superiority Test for a Binomial Proportion

A superiority test corresponds to an upper one-sided test with a positive-valued margin, as demonstrated in the following statements: 

proc power;
   onesamplefreq test=exact
      sides = U
      proportion = 0.15
      nullproportion = 0.1
      margin = 0.02
      ntotal = 130
      power = .;
run;
Confidence Interval Precision

The following statements performs a confidence interval precision analysis for the Wilson score-based confidence interval for a binomial proportion. The default value of the ALPHA= option specifies a confidence level of 0.95. 

proc power;
   onesamplefreq ci=wilson
      halfwidth = 0.1
      proportion = 0.3
      ntotal = 70
      probwidth = .;
run;

Restrictions on Option Combinations

To specify the equivalence bounds for TEST= EQUIV_ADJZ, TEST= EQUIV_EXACT, and TEST= EQUIV_Z, use any of these three option sets: