The POWER Procedure
- Overview
-
Getting Started

-
Syntax
 PROC POWER StatementCOXREG StatementLOGISTIC StatementMULTREG StatementONECORR StatementONESAMPLEFREQ StatementONESAMPLEMEANS StatementONEWAYANOVA StatementPAIREDFREQ StatementPAIREDMEANS StatementPLOT StatementTWOSAMPLEFREQ StatementTWOSAMPLEMEANS StatementTWOSAMPLESURVIVAL StatementTWOSAMPLEWILCOXON Statement
PROC POWER StatementCOXREG StatementLOGISTIC StatementMULTREG StatementONECORR StatementONESAMPLEFREQ StatementONESAMPLEMEANS StatementONEWAYANOVA StatementPAIREDFREQ StatementPAIREDMEANS StatementPLOT StatementTWOSAMPLEFREQ StatementTWOSAMPLEMEANS StatementTWOSAMPLESURVIVAL StatementTWOSAMPLEWILCOXON Statement -
Details

-
Examples
 One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test
One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test - References
Overview of Power Concepts
In statistical hypothesis testing, you typically express the belief that some effect exists in a population by specifying
an alternative hypothesis 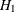 . You state a null hypothesis
. You state a null hypothesis 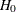 as the assertion that the effect does not exist and attempt to gather evidence to reject
as the assertion that the effect does not exist and attempt to gather evidence to reject 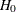 in favor of
in favor of 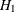 . Evidence is gathered in the form of sample data, and a statistical test is used to assess
. Evidence is gathered in the form of sample data, and a statistical test is used to assess 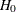 . If
. If 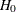 is rejected but there really is no effect, this is called a Type I error. The probability of a Type I error is usually designated "alpha" or
is rejected but there really is no effect, this is called a Type I error. The probability of a Type I error is usually designated "alpha" or  , and statistical tests are designed to ensure that
, and statistical tests are designed to ensure that  is suitably small (for example, less than 0.05).
is suitably small (for example, less than 0.05).
If there really is an effect in the population but 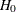 is not rejected in the statistical test, then a Type II error has been made. The probability of a Type II error is usually designated "beta" or
is not rejected in the statistical test, then a Type II error has been made. The probability of a Type II error is usually designated "beta" or 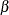 . The probability 1 –
. The probability 1 – 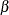 of avoiding a Type II error—that is, correctly rejecting
of avoiding a Type II error—that is, correctly rejecting 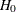 and achieving statistical significance—is called the power. (
Note: Another more general definition of power is the probability of rejecting
and achieving statistical significance—is called the power. (
Note: Another more general definition of power is the probability of rejecting 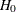 for any given set of circumstances, even those that correspond to
for any given set of circumstances, even those that correspond to 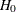 being true. The POWER procedure uses this more general definition.)
being true. The POWER procedure uses this more general definition.)
An important goal in study planning is to ensure an acceptably high level of power. Sample size plays a prominent role in power computations because the focus is often on determining a sufficient sample size to achieve a certain power, or assessing the power for a range of different sample sizes.
Some of the analyses in the POWER procedure focus on precision rather than power. An analysis of confidence interval precision is analogous to a traditional power analysis, with "CI Half-Width" taking the place of effect size and "Prob(Width)" taking the place of power. The CI Half-Width is the margin of error associated with the confidence interval, the distance between the point estimate and an endpoint. The Prob(Width) is the probability of obtaining a confidence interval with at most a target half-width.