The POWER Procedure

Agresti, A. (1980). “Generalized Odds Ratios for Ordinal Data.” Biometrics 36:59–67.

Agresti, A., and Coull, B. A. (1998). “Approximate Is Better Than 'Exact' for Interval Estimation of Binomial Proportions.” American Statistician 52:119–126.

Anderson, T. W. (1984). An Introduction to Multivariate Statistical Analysis. 2nd ed. New York: John Wiley & Sons.

Beal, S. L. (1989). “Sample Size Determination for Confidence Intervals on the Population Means and on the Difference between Two Population Means.” Biometrics 45:969–977.

Blackwelder, W. C. (1982). “'Proving the Null Hypothesis' in Clinical Trials.” Controlled Clinical Trials 3:345–353.

Brown, L. D., Cai, T. T., and DasGupta, A. (2001). “Interval Estimation for a Binomial Proportion.” Statistical Science 16:101–133.

Cantor, A. B. (1997). Extending SAS Survival Analysis Techniques for Medical Research. Cary, NC: SAS Institute Inc.

Castelloe, J. M. (2000). “Sample Size Computations and Power Analysis with the SAS System.” In Proceedings of the Twenty-Fifth Annual SAS Users Group International Conference. Cary, NC: SAS Institute Inc. http://www2.sas.com/proceedings/sugi25/25/st/25p265.pdf.

Castelloe, J. M., and O’Brien, R. G. (2001). “Power and Sample Size Determination for Linear Models.” In Proceedings of the Twenty-Sixth Annual SAS Users Group International Conference. Cary, NC: SAS Institute Inc. http://www2.sas.com/proceedings/sugi26/p240-26.pdf.

Chernick, M. R., and Liu, C. Y. (2002). “The Saw-Toothed Behavior of Power versus Sample Size and Software Solutions: Single Binomial Proportion Using Exact Methods.” American Statistician 56:149–155.

Chow, S.-C., Shao, J., and Wang, H. (2003). Sample Size Calculations in Clinical Research. Boca Raton, FL: CRC Press.

Connor, R. J. (1987). “Sample Size for Testing Differences in Proportions for the Paired-Sample Design.” Biometrics 43:207–211.

Diegert, C., and Diegert, K. V. (1981). “Note on Inversion of Casagrande-Pike-Smith Approximate Sample-Size Formula for Fisher-Irwin Test on 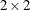Tables.” Biometrics 37:595.

Diletti, D., Hauschke, D., and Steinijans, V. W. (1991). “Sample Size Determination for Bioequivalence Assessment by Means of Confidence Intervals.” International Journal of Clinical Pharmacology, Therapy, and Toxicology 29:1–8.

DiSantostefano, R. L., and Muller, K. E. (1995). “A Comparison of Power Approximations for Satterthwaite’s Test.” Communications in Statistics—Simulation and Computation 24:583–593.

Farrington, C. P., and Manning, G. (1990). “Test Statistics and Sample Size Formulae for Comparative Binomial Trials with Null Hypothesis of Non-zero Risk Difference or Non-unity Relative Risk.” Statistics in Medicine 9:1447–1454.

Fisher, R. A. (1921). “On the 'Probable Error' of a Coefficient of Correlation Deduced from a Small Sample.” Metron 1:3–32.

Fleiss, J. L., Tytun, A., and Ury, H. K. (1980). “A Simple Approximation for Calculating Sample Sizes for Comparing Independent Proportions.” Biometrics 36:343–346.

Gatsonis, C., and Sampson, A. R. (1989). “Multiple Correlation: Exact Power and Sample Size Calculations.” Psychological Bulletin 106:516–524.

Hocking, R. R. (1985). The Analysis of Linear Models. Monterey, CA: Brooks/Cole.

Hsieh, F. Y. (1989). “Sample Size Tables for Logistic Regression.” Statistics in Medicine 8:795–802.

Hsieh, F. Y., and Lavori, P. W. (2000). “Sample-Size Calculations for the Cox Proportional Hazards Regression Model with Nonbinary Covariates.” Controlled Clinical Trials 21:552–560.

Johnson, N. L., and Kotz, S. (1970). Distributions in Statistics: Continuous Univariate Distributions. New York: John Wiley & Sons.

Johnson, N. L., Kotz, S., and Balakrishnan, N. (1994). Continuous Univariate Distributions. 2nd ed. Vol. 1. New York: John Wiley & Sons.

Johnson, N. L., Kotz, S., and Balakrishnan, N. (1995). Continuous Univariate Distributions. 2nd ed. Vol. 2. New York: John Wiley & Sons.

Johnson, N. L., Kotz, S., and Kemp, A. W. (1992). Univariate Discrete Distributions. 2nd ed. New York: John Wiley & Sons.

Jones, R. M., and Miller, K. S. (1966). “On the Multivariate Lognormal Distribution.” Journal of Industrial Mathematics 16:63–76.

Kolassa, J. E. (1995). “A Comparison of Size and Power Calculations for the Wilcoxon Statistic for Ordered Categorical Data.” Statistics in Medicine 14:1577–1581.

Kotz, S., Balakrishnan, N., and Johnson, N. L. (2000). Continuous Multivariate Distributions. 2nd ed. New York: Wiley-Interscience.

Lachin, J. M. (1992). “Power and Sample Size Evaluation for the McNemar Test with Application to Matched Case-Control Studies.” Statistics in Medicine 11:1239–1251.

Lakatos, E. (1988). “Sample Sizes Based on the Log-Rank Statistic in Complex Clinical Trials.” Biometrics 44:229–241.

Lenth, R. V. (2001). “Some Practical Guidelines for Effective Sample Size Determination.” American Statistician 55:187–193.

Maxwell, S. E. (2000). “Sample Size and Multiple Regression Analysis.” Psychological Methods 5:434–458.

Miettinen, O. S. (1968). “The Matched Pairs Design in the Case of All-or-None Responses.” Biometrics 24:339–352.

Moser, B. K., Stevens, G. R., and Watts, C. L. (1989). “The Two-Sample T Test versus Satterthwaite’s Approximate F Test.” Communications in Statistics—Theory and Methods 18:3963–3975.

Muller, K. E., and Benignus, V. A. (1992). “Increasing Scientific Power with Statistical Power.” Neurotoxicology and Teratology 14:211–219.

O’Brien, R. G., and Castelloe, J. M. (2006). “Exploiting the Link between the Wilcoxon-Mann-Whitney Test and a Simple Odds Statistic.” In Proceedings of the Thirty-First Annual SAS Users Group International Conference. Cary, NC: SAS Institute Inc. http://www2.sas.com/proceedings/sugi31/209-31.pdf.

O’Brien, R. G., and Castelloe, J. M. (2007). “Sample-Size Analysis for Traditional Hypothesis Testing: Concepts and Issues.” In Pharmaceutical Statistics Using SAS: A Practical Guide, edited by A. Dmitrienko, C. Chuang-Stein, and R. D’Agostino, 237–271. Cary, NC: SAS Institute Inc.

O’Brien, R. G., and Muller, K. E. (1993). “Unified Power Analysis for t-Tests through Multivariate Hypotheses.” In Applied Analysis of Variance in Behavioral Science, edited by L. K. Edwards, 297–344. New York: Marcel Dekker.

Owen, D. B. (1965). “A Special Case of a Bivariate Non-central t-Distribution.” Biometrika 52:437–446.

Pagano, M., and Gauvreau, K. (1993). Principles of Biostatistics. Belmont, CA: Wadsworth.

Phillips, K. F. (1990). “Power of the Two One-Sided Tests Procedure in Bioequivalence.” Journal of Pharmacokinetics and Biopharmaceutics 18:137–144.

Satterthwaite, F. E. (1946). “An Approximate Distribution of Estimates of Variance Components.” Biometrics Bulletin 2:110–114.

Schork, M. A., and Williams, G. W. (1980). “Number of Observations Required for the Comparison of Two Correlated Proportions.” Communications in Statistics—Simulation and Computation 9:349–357.

Schuirmann, D. J. (1987). “A Comparison of the Two One-Sided Tests Procedure and the Power Approach for Assessing the Equivalence of Average Bioavailability.” Journal of Pharmacokinetics and Biopharmaceutics 15:657–680.

Self, S. G., Mauritsen, R. H., and Ohara, J. (1992). “Power Calculations for Likelihood Ratio Tests in Generalized Linear Models.” Biometrics 48:31–39.

Senn, S. (1993). Cross-over Trials in Clinical Research. New York: John Wiley & Sons.

Shieh, G. (2000). “A Comparison of Two Approaches for Power and Sample Size Calculations in Logistic Regression Models.” Communications in Statistics—Simulation and Computation 29:763–791.

Shieh, G., and O’Brien, R. G. (1998). “A Simpler Method to Compute Power for Likelihood Ratio Tests in Generalized Linear Models.” In Proceedings of the Annual Joint Statistical Meetings of the American Statistical Association. Alexandria, VA: American Statistical Association.

Stuart, A., and Ord, J. K. (1994). Distribution Theory. Vol. 1 of Kendall’s Advanced Theory of Statistics. 6th ed. Baltimore: Edward Arnold Publishers.

Walters, D. E. (1979). “In Defence of the Arc Sine Approximation.” The Statistician 28:219–232.

Wellek, S. (2003). Testing Statistical Hypotheses of Equivalence. Boca Raton, FL: Chapman & Hall/CRC.