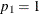The POWER Procedure

Analyses in the MULTREG Statement

Type III F Test in Multiple Regression (TEST=TYPE3)

Maxwell (2000) discusses a number of different ways to represent effect sizes (and to compute exact power based on them) in multiple regression. PROC POWER supports two of these, multiple partial correlation and 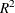$R^2$ in full and reduced models.

Let p denote the total number of predictors in the full model (excluding the intercept), and let Y denote the response variable. You are testing that the coefficients of 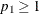$p_1 \ge 1$ predictors in a set 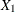$X_1$ are 0, controlling for all of the other predictors 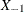$X_{-1}$ , which consists of 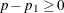$p-p_1 \ge 0$ variables.

The hypotheses can be expressed in two different ways. The first is in terms of 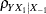$\rho _{Y X_1|X_{-1}}$ , the multiple partial correlation between the predictors in 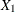$X_1$ and the response Y adjusting for the predictors in $X_{-1}$ :

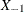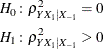
$\begin{align*} H_{0}\colon & \rho ^2_{Y X_1|X_{-1}} = 0 \\ H_{1}\colon & \rho ^2_{Y X_1|X_{-1}} > 0 \end{align*}$

The second is in terms of the multiple correlations in full (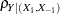 $\rho _{Y|(X_1,X_{-1})}$ ) and reduced ( 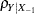$\rho _{Y|X_{-1}}$ ) nested models:

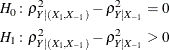
$\begin{align*} H_{0}\colon & \rho ^2_{Y|(X_1,X_{-1})} - \rho ^2_{Y|X_{-1}} = 0 \\ H_{1}\colon & \rho ^2_{Y|(X_1,X_{-1})} - \rho ^2_{Y|X_{-1}} > 0 \\ \end{align*}$

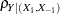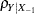Note that the squared values of $\rho _{Y|(X_1,X_{-1})}$ and $\rho _{Y|X_{-1}}$ are the population 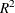$R^2$ values for full and reduced models.

The test statistic can be written in terms of the sample multiple partial correlation 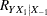$R_{Y X_1|X_{-1}}$ ,

$F = \left\{ \begin{array}{ll} (N-1-p) \frac{R^2_{Y X_1|X_{-1}}}{1 - R^2_{Y X_1|X_{-1}}}, & \mbox{intercept} \\ (N-p) \frac{R^2_{Y X_1|X_{-1}}}{1 - R^2_{Y X_1|X_{-1}}}, & \mbox{no intercept} \\ \end{array} \right. \\$

or the sample multiple correlations in full (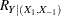 $R_{Y|(X_1,X_{-1})}$ ) and reduced ( 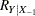$R_{Y|X_{-1}}$ ) models,

$F = \left\{ \begin{array}{ll} (N-1-p) \frac{R^2_{Y|(X_1,X_{-1})} - R^2_{Y|X_{-1}}}{1 - R^2_{Y|(X_1,X_{-1})}}, & \mbox{intercept} \\ (N-p) \frac{R^2_{Y|(X_1,X_{-1})} - R^2_{Y|X_{-1}}}{1 - R^2_{Y|(X_1,X_{-1})}}, & \mbox{no intercept} \\ \end{array} \right. \\$

The test is the usual Type III F test in multiple regression:

$\mbox{Reject} \quad H_0 \quad \mbox{if} \left\{ \begin{array}{ll} F \ge F_{1-\alpha }(p_1, N-1-p), & \mbox{intercept} \\ F \ge F_{1-\alpha }(p_1, N-p), & \mbox{no intercept} \\ \end{array} \right.$

Although the test is invariant to whether the predictors are assumed to be random or fixed, the power is affected by this assumption. If the response and predictors are assumed to have a joint multivariate normal distribution, then the exact power is given by the following formula:

$\begin{align*} \mr{power} & = \left\{ \begin{array}{ll} P\left[\left(\frac{N-1-p}{p_1}\right) \left( \frac{R^2_{Y X_1|X_{-1}}}{1 - R^2_{Y X_1|X_{-1}}} \right) \ge F_{1-\alpha }(p_1, N-1-p)\right], & \mbox{intercept} \\ P\left[\left(\frac{N-p}{p_1}\right) \left( \frac{R^2_{Y X_1|X_{-1}}}{1 - R^2_{Y X_1|X_{-1}}} \right) \ge F_{1-\alpha }(p_1, N-p)\right], & \mbox{no intercept} \\ \end{array} \right. \\ & = \left\{ \begin{array}{ll} P\left[ R^2_{Y X_1|X_{-1}} \ge \frac{F_{1-\alpha }(p_1, N-1-p)}{F_{1-\alpha }(p_1, N-1-p) + \frac{N-1-p}{p_1}} \right], & \mbox{intercept} \\ P\left[ R^2_{Y X_1|X_{-1}} \ge \frac{F_{1-\alpha }(p_1, N-p)}{F_{1-\alpha }(p_1, N-p) + \frac{N-p}{p_1}} \right], & \mbox{no intercept} \\ \end{array} \right. \\ \end{align*}$

The distribution of 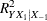$R^2_{Y X_1|X_{-1}}$ (for any 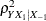$\rho ^2_{Y X_1|X_{-1}}$ ) is given in Chapter 32 of Johnson, Kotz, and Balakrishnan (1995). Sample size tables are presented in Gatsonis and Sampson (1989).

If the predictors are assumed to have fixed values, then the exact power is given by the noncentral F distribution. The noncentrality parameter is

$\lambda = N \frac{\rho ^2_{Y X_1|X_{-1}}}{1 - \rho ^2_{Y X_1|X_{-1}}}$

or equivalently,

$\lambda = N \frac{\rho ^2_{Y|(X_1,X_{-1})} - \rho ^2_{Y|X_{-1}}}{1 - \rho ^2_{Y|(X_1,X_{-1})}}$

The power is

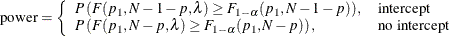
$\begin{align*} \mr{power} & = \left\{ \begin{array}{ll} P\left(F(p_1, N-1-p, \lambda ) \ge F_{1-\alpha }(p_1, N-1-p)\right), & \mbox{intercept} \\ P\left(F(p_1, N-p, \lambda ) \ge F_{1-\alpha }(p_1, N-p)\right), & \mbox{no intercept} \\ \end{array} \right. \\ \end{align*}$

The minimum acceptable input value of N depends on several factors, as shown in Table 89.32.

Table 89.32: Minimum Acceptable Sample Size Values in the MULTREG Statement

Predictor Type	Intercept in Model?	$p_1=1$ ?	Minimum N
Random	Yes	Yes	p + 3
Random	Yes	No	p + 2
Random	No	Yes	p + 2
Random	No	No	p + 1
Fixed	Yes	Yes or No	p + 2
Fixed	No	Yes or No	p + 1