The KDE Procedure

ODS Graphics

Subsections:

ODS Graph Names
Bivariate Plots
Univariate Plots
Binning of Bivariate Histogram

Statistical procedures use ODS Graphics to create graphs as part of their output. ODS Graphics is described in detail in Chapter 21: Statistical Graphics Using ODS.

Before you create graphs, ODS Graphics must be enabled (for example, by specifying the ODS GRAPHICS ON statement). For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.

The overall appearance of graphs is controlled by ODS styles. Styles and other aspects of using ODS Graphics are discussed in the section A Primer on ODS Statistical Graphics in Chapter 21: Statistical Graphics Using ODS.

ODS Graph Names

PROC KDE assigns a name to each graph it creates using the Output Delivery System (ODS). You can use these names to reference the graphs when using ODS. The names are listed in Table 66.4.

Table 66.4: Graphs Produced by PROC KDE

ODS Graph Name	Plot Description	Statement	PLOTS= Option
BivariateHistogram	Bivariate histogram of data	BIVAR	HISTOGRAM
ContourPlot	Contour plot of bivariate kernel density estimate	BIVAR	CONTOUR
ContourScatterPlot	Contour plot of bivariate kernel density estimate overlaid with scatter plot	BIVAR	CONTOURSCATTER
DensityPlot	Univariate kernel density estimate curve	UNIVAR	DENSITY
DensityOverlayPlot	Overlaid univariate kernel density estimate curves	UNIVAR	DENSITYOVERLAY
HistogramDensity	Univariate histogram overlaid with kernel density estimate curve	UNIVAR	HISTDENSITY
Histogram	Univariate histogram of data	UNIVAR	HISTOGRAM
HistogramSurface	Bivariate histogram overlaid with surface plot of bivariate kernel density estimate	BIVAR	HISTSURFACE
ScatterPlot	Scatter plot of data	BIVAR	SCATTER
SurfacePlot	Surface plot of bivariate kernel density estimate	BIVAR	SURFACE

Bivariate Plots

You can specify the PLOTS= option in the BIVAR statement to request graphical displays of bivariate kernel density estimates.

PLOTS= option1 <option2 …>: requests one or more plots of the bivariate kernel density estimate. The following table shows the available plot options.

Option	Description
ALL	all available displays
CONTOUR	contour plot of bivariate density estimate
CONTOURSCATTER	contour plot of bivariate density estimate overlaid with scatter plot of data
HISTOGRAM	bivariate histogram of data
HISTSURFACE	bivariate histogram overlaid with bivariate kernel density estimate
NONE	suppresses all plots
SCATTER	scatter plot of data
SURFACE	surface plot of bivariate kernel density estimate

By default, if ODS Graphics is enabled and you do not specify the PLOTS= option, then the BIVAR statement creates a contour plot. If you specify the PLOTS= option, you get only the requested plots.

Univariate Plots

You can specify the PLOTS= option in the UNIVAR statement to request graphical displays of univariate kernel density estimates.

PLOTS= option1 <option2 …>: requests one or more plots of the univariate kernel density estimate. The following table shows the available plot options.

Option	Description
ALL	all available displays
DENSITY	univariate kernel density estimate curve
DENSITYOVERLAY	overlaid univariate kernel density estimate curves
HISTDENSITY	univariate histogram of data overlaid with kernel density estimate curve
HISTOGRAM	univariate histogram of data
NONE	suppresses all plots

By default, if ODS Graphics is enabled and you do not specify the PLOTS= option, then the UNIVAR statement creates a histogram overlaid with a kernel density estimate. If you specify the PLOTS= option, you get only the requested plots.

Binning of Bivariate Histogram

Let 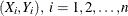$(X_{i},Y_{i}), \ i = 1,2, \ldots , n$ , be a sample of size n drawn from a bivariate distribution. For the marginal distribution of 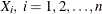$X_{i}, \ i = 1,2, \ldots , n$ , the number of bins ( 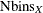$\mr{Nbins}_{X}$ ) in the bivariate histogram is calculated according to the formula

$\mr{Nbins}_{X} = \mr{ceil} \left(\mr{range}_{X} / \mr{width}_{X} \right)$

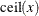where $\mr{ceil}(x)$ denotes the smallest integer greater than or equal to x,

$\mr{range}_{X} = \max _{1 \leq i \leq n}(X_ i) - \min _{1 \leq i \leq n}(X_ i)$

and the optimal bin width is obtained, following Scott (1992, p. 84), as

$\mr{width}_{X} = 3.504 \ \hat{\sigma }_{X} (1 - \hat{\rho }^{2})^{3/8} n^{-1/4}$

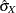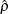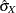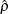Here, $\hat{\sigma }_{X}$ and $\hat{\rho }$ are the sample variance and the sample correlation coefficient, respectively. When you specify a WEIGHT variable, PROC KDE uses weighted versions of $\hat{\sigma }_{X}$ and $\hat{\rho }$ in the preceding expressions.

Similar formulas are used to compute the number of bins for the marginal distribution of 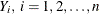$Y_{i}, \ i = 1,2, \ldots , n$ . Further details can be found in Scott (1992).

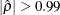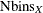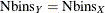Notice that if $|\hat{\rho }| > 0.99$ , then $\mr{Nbins}_{X}$ is calculated as in the univariate case (see Terrell and Scott 1985). In this case $\mr{Nbins}_{Y} = \mr{Nbins}_{X}$ .