The KDE Procedure
Kernel Density Estimates
A weighted univariate kernel density estimate involves a variable X and a weight variable W. Let 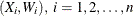 , denote a sample of X and W of size n. The weighted kernel density estimate of
, denote a sample of X and W of size n. The weighted kernel density estimate of 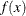 , the density of X, is as follows:
, the density of X, is as follows:
![\[ \hat{f}(x) = \frac{1}{\sum _{i=1}^{n} W_{i}} \sum _{i=1}^{n} W_{i} \varphi _{h}(x-X_{i}) \]](images/statug_kde0006.png)
where h is the bandwidth and
![\[ \varphi _{h}(x) = \frac{1}{\sqrt {2\pi }h} \exp \left( -\frac{x^{2}}{2h^{2}} \right) \]](images/statug_kde0007.png)
is the standard normal density rescaled by the bandwidth. If 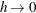 and
and 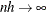 , then the optimal bandwidth is
, then the optimal bandwidth is
![\[ h_\mr {AMISE} = \left[ \frac{1}{2\sqrt {\pi } n \int (f'')^{2}} \right]^{1/5} \]](images/statug_kde0010.png)
This optimal value is unknown, and so approximations methods are required. For a derivation and discussion of these results, see Silverman (1986, Chapter 3) and Jones, Marron, and Sheather (1996).
For the bivariate case, let 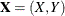 be a bivariate random element taking values in
be a bivariate random element taking values in 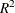 with joint density function
with joint density function
![\[ f(x,y), \ (x,y) \in R^2 \]](images/statug_kde0013.png)
and let 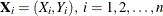 , be a sample of size n drawn from this distribution. The kernel density estimate of
, be a sample of size n drawn from this distribution. The kernel density estimate of 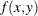 based on this sample is
based on this sample is
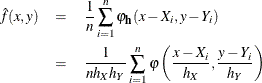
where 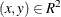 ,
, 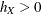 and
and 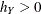 are the bandwidths, and
are the bandwidths, and 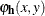 is the rescaled normal density
is the rescaled normal density
![\[ \varphi _{\mb{h}}(x,y) = \frac{1}{ h_{X}h_{Y}} \varphi \left( \frac{x}{h_{X}}, \frac{y}{h_{Y}} \right) \]](images/statug_kde0021.png)
where 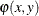 is the standard normal density function
is the standard normal density function
![\[ \varphi (x,y) = \frac{1}{2\pi } \exp \left( -\frac{x^{2}+y^{2}}{2} \right) \]](images/statug_kde0023.png)
Under mild regularity assumptions about 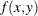 , the mean integrated squared error (MISE) of
, the mean integrated squared error (MISE) of 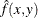 is
is
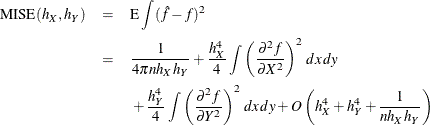
as 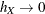 ,
, 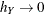 and
and 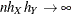 .
.
Now set
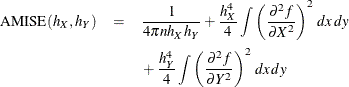
which is the asymptotic mean integrated squared error (AMISE). For fixed n, this has a minimum at 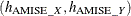 defined as
defined as
![\[ h_{\mr{AMISE}\_ X} = \left[\frac{\int (\frac{\partial ^{2}f}{\partial X^{2}})^{2}}{4n\pi }\right]^{1/6} \left[\frac{\int (\frac{\partial ^{2}f}{\partial X^{2}})^{2}}{\int (\frac{\partial ^{2}f}{\partial Y^{2}})^{2}}\right]^{2/3} \]](images/statug_kde0031.png)
and
![\[ h_{\mr{AMISE}\_ Y} = \left[\frac{\int (\frac{\partial ^{2}f}{\partial Y^{2}})^{2}}{4n\pi }\right]^{1/6} \left[\frac{\int (\frac{\partial ^{2}f}{\partial Y^{2}})^{2}}{\int (\frac{\partial ^{2}f}{\partial X^{2}})^{2}}\right]^{2/3} \]](images/statug_kde0032.png)
These are the optimal asymptotic bandwidths in the sense that they minimize MISE. However, as in the univariate case, these
expressions contain the second derivatives of the unknown density 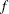 being estimated, and so approximations are required. See Wand and Jones (1993) for further details.
being estimated, and so approximations are required. See Wand and Jones (1993) for further details.
