The KDE Procedure
Fast Fourier Transform
As shown in the last subsection, kernel density estimates can be expressed as a submatrix of a certain convolution. The fast Fourier transform (FFT) is a computationally effective method for computing such convolutions. For a reference on this material, see Press et al. (1988).
The discrete Fourier transform of a complex vector 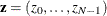 is the vector
is the vector 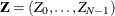 , where
, where
![\[ Z_{j}=\sum _{l=0}^{N-1}z_{l}e^{2\pi i l j/N}, \quad j=0,\ldots ,N-1 \]](images/statug_kde0087.png)
and i is the square root of –1. The vector  can be recovered from
can be recovered from 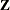 by applying the inverse discrete Fourier transform formula
by applying the inverse discrete Fourier transform formula
![\[ z_{l}=N^{-1}\sum _{j=0}^{N-1}Z_{j}e^{-2\pi i l j/N}, \quad l=0,\ldots ,N-1 \]](images/statug_kde0090.png)
Discrete Fourier transforms and their inverses can be computed quickly using the FFT algorithm, especially when N is highly composite; that is, it can be decomposed into many factors, such as a power of 2. By the discrete convolution theorem, the convolution of two vectors is the inverse Fourier transform of the element-by-element product of their Fourier transforms.
This, however, requires certain periodicity assumptions, which explains why the vectors 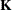 and
and 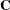 require zero-padding. This is to avoid wrap-around effects (see Press et al.; 1988, pp. 410–411). The vector
require zero-padding. This is to avoid wrap-around effects (see Press et al.; 1988, pp. 410–411). The vector 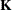 is actually mirror-imaged so that the convolution of
is actually mirror-imaged so that the convolution of 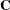 and
and 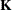 will be the vector of binned estimates. Thus, if S denotes the inverse Fourier transform of the element-by-element product of the Fourier transforms of
will be the vector of binned estimates. Thus, if S denotes the inverse Fourier transform of the element-by-element product of the Fourier transforms of 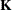 and
and 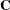 , then the first g elements of S are the estimates.
, then the first g elements of S are the estimates.
The bivariate Fourier transform of an 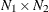 complex matrix having
complex matrix having 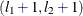 entry equal to
entry equal to 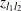 is the
is the 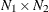 matrix with
matrix with 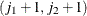 entry given by
entry given by
![\[ Z_{j_{1}j_{2}}=\sum _{l_{1}=0}^{N_{1}-1} \sum _{l_{2}=0}^{N_{2}-1} z_{l_{1}l_{2}} e^{2\pi i(l_{1}j_{1}/N_{1}+l_{2}j_{2}/N_{2})} \]](images/statug_kde0095.png)
and the formula of the inverse is
![\[ z_{l_{1}l_{2}}=(N_{1}N_{2})^{-1} \sum _{j_{1}=0}^{N_{1}-1} \sum _{j_{2}=0}^{N_{2}-1} Z_{j_{1}j_{2}} e^{-2\pi i(l_{1}j_{1}/N_{1}+l_{2}j_{2}/N_{2})} \]](images/statug_kde0096.png)
The same discrete convolution theorem applies, and zero-padding is needed for matrices 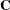 and
and 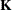 . In the case of
. In the case of 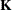 , the matrix is mirror-imaged twice. Thus, if S denotes the inverse Fourier transform of the element-by-element product of the Fourier transforms of
, the matrix is mirror-imaged twice. Thus, if S denotes the inverse Fourier transform of the element-by-element product of the Fourier transforms of 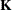 and
and 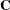 , then the upper-left
, then the upper-left 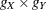 corner of S contains the estimates.
corner of S contains the estimates.
