The KDE Procedure

Binning

Binning, or assigning data to discrete categories, is an effective and fast method for large data sets (Fan and Marron 1994). When the sample size n is large, direct evaluation of the kernel estimate 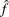$\hat f$ at any point would involve n kernel evaluations, as shown in the preceding formulas. To evaluate the estimate at each point of a grid of size g would thus require 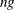$ng$ kernel evaluations. When you use g = 401 in the univariate case or 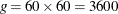$g = 60\times 60 = 3600$ in the bivariate case and 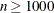$n\geq 1000$ , the amount of computation can be prohibitively large. With binning, however, the computational order is reduced to g, resulting in a much quicker algorithm that is nearly as accurate as direct evaluation.

To bin a set of weighted univariate data 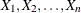$X_{1},X_{2},\ldots ,X_{n}$ to a grid 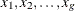$x_{1}, x_{2},\ldots ,x_{g}$ , simply assign each sample 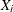$X_{i}$ , together with its weight 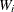$W_{i}$ , to the nearest grid point 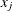$x_{j}$ (also called the bin center). When binning is completed, each grid point 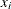$x_{i}$ has an associated number 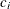$c_{i}$ , which is the sum total of all the weights that correspond to sample points that have been assigned to 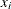$x_{i}$ . These 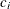$c_{i}$ s are known as the bin counts.

This procedure replaces the data 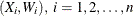$(X_{i},W_{i}), \ i=1,2,\ldots ,n$ , with the smaller set 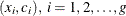$(x_{i},c_{i}), \ i = 1,2,\ldots ,g$ , and the estimation is carried out with these new data. This is so-called simple binning, versus the finer linear binning described in Wand (1994). PROC KDE uses simple binning for the sake of faster and easier implementation. Also, it is assumed that the bin centers 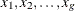$x_{1},x_{2},\ldots ,x_{g}$ are equally spaced and in increasing order. 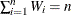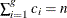In addition, assume for notational convenience that $\sum _{i=1}^ nW_{i} = n$ and, therefore, $\sum _{i=1}^ gc_{i} = n$ .

If you replace the data 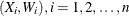$(X_{i},W_{i}), i=1,2,\ldots ,n$ , with 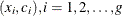$(x_{i},c_{i}), i = 1,2,\ldots ,g$ , the weighted estimator 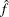$\hat{f}$ then becomes

$\hat{f}(x) = \frac{1}{n}\sum _{i=1}^{g} c_{i} \varphi _{h}(x-x_{i})$

with the same notation as used previously. To evaluate this estimator at the g points of the same grid vector 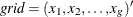$\mi{grid} = (x_{1},x_{2},\ldots ,x_{g})’$ is to calculate

$\hat{f}(x_{i}) = \frac{1}{n}\sum _{j=1}^{g} c_{j} \varphi _{h}(x_{i}-x_{j})$

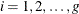for $i = 1,2,\ldots ,g$ . This can be rewritten as

$\hat{f}(x_{i}) = \frac{1}{n}\sum _{j=1}^{g} c_{j} \varphi _{h}(|i-j|\delta )$

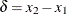where $\delta = x_{2}-x_{1}$ is the increment of the grid.

The same idea of binning works similarly with bivariate data, where you estimate 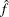$\hat{f}$ over the grid matrix 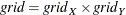$\mi{grid}=\mi{grid}_{X}\times \mi{grid}_{Y}$ as follows:

$\mi{grid} = \left[ \begin{array}{cccc} \mb{x}_{1,1} & \mb{x}_{1,2} & \ldots & \mb{x}_{1,g_{Y}} \\ \mb{x}_{2,1} & \mb{x}_{2,2} & \ldots & \mb{x}_{2,g_{Y}} \\ \vdots \\ \mb{x}_{g_{X},1} & \mb{x}_{g_{X},2} & \ldots & \mb{x}_{g_{X},g_{Y}} \end{array} \right]$

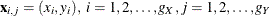where $\mb{x}_{i,j}=(x_{i},y_{i}), \ i = 1,2,\ldots ,g_{X}, j=1,2,\ldots ,g_{Y}$ , and the estimates are

$\hat{f}(\mb{x}_{i,j}) = \frac{1}{n}\sum _{k=1}^{g_{X}} \sum _{l=1}^{g_{Y}} c_{k,l}\varphi _{\mb{h}}(|i-k|\delta _{X},|j-l|\delta _{Y})$

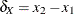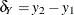where $\delta _{X} = x_{2}-x_{1}$ and $\delta _{Y} = y_{2}-y_{1}$ are the increments of the grid.