The HPQUANTSELECT Procedure

Quantile Regression

Subsections:

This section describes the basic concepts and notations for quantile regression and quantile regression model selection.

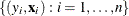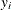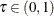Let $\{ (y_ i,\mb{x}_ i):i=1,\ldots ,n\}$ denote a data set of observations, where $y_ i$ are responses and $\mb{x}_ i$ are regressors. Koenker and Bassett (1978) define the regression quantile at quantile level $\tau \in (0,1)$ as any solution to the minimization problem

$\min _{\bbeta \in \mb{R}^ p} \sum _{i=1}^ n \rho _\tau \left(y_ i-\mb{x}_ i^{\prime }\bbeta \right)$

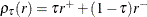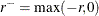where $\rho _\tau (r)=\tau r^+ +(1-\tau )r^-$ is a check loss function in which $r^+=\max (r,0)$ and $r^-=\max (-r,0)$ .

If you specify weights 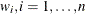$w_ i, i=1,\ldots ,n$ , in the WEIGHT statement, then weighted quantile regression is carried out by solving

$\min _{\bbeta \in \mb{R}^ p} \sum _{i=1}^ n \rho _\tau \left(w_ i(y_ i-\mb{x}_ i^{\prime }\bbeta )\right)$

The HPQUANTSELECT procedure fits a quantile regression model by using a predictor-corrector interior point algorithm, which was originally designed to solve support vector machine classifiers for large data sets (Gertz and Griffin 2005, 2010).