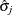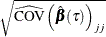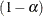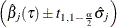The HPQUANTSELECT Procedure

More Statistics for Parameter Estimates

Let 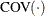$\mbox{COV}(\cdot )$ denote the covariance function matrix of a random vector. Then, the sparsity-function estimates of 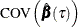$\mbox{COV}\left(\hat{\bbeta }(\tau )\right)$ is

\[ \widehat{\mbox{COV}}\left(\hat{\bbeta }(\tau )\right)=\left\{ \begin{array}{l l} \omega ^2(\tau , F)\bOmega ^{-1}/n & \mbox{for a linear model with iid errors}\\ \tau (1-\tau )\mb{H}_ n^{-}\bOmega \mb{H}_ n^{-})/n & \mbox{for a linear-in-parameter model with non-iid settings} \end{array} \right. \]

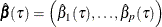where ${\hat{\bbeta }}(\tau )=\left(\hat{\beta }_1(\tau ),\ldots ,\hat{\beta }_ p(\tau )\right)$ is the vector of the parameter estimates.

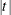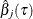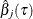If you specify the CLB option in the MODEL statement, PROC HPQUANTSELECT outputs the standard error, confidence limits, t value, and Pr > $|t|$ probability for each $\hat{\beta }_ j(\tau )$ in the parameter estimates table. Table 59.5 summarizes these statistics for $\hat{\beta }_ j(\tau )$.

Table 59.5: More Statistics for 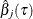$\hat{\beta }_ j(\tau )$

Statistic

  

Definition

Standard error: $\hat{\sigma }_ j$

 

$\sqrt {\widehat{\mbox{COV}}\left(\hat{\bbeta }(\tau )\right)_{jj}}$

$(1-\alpha )$% confidence limits

 

$\left(\hat{\beta }_ j(\tau )\pm t_{1,1-{\alpha \over 2}} \hat{\sigma }_ j \right)$

t value

 

$\hat{\beta }_ j(\tau ) / \hat{\sigma }_ j$

Pr > $|t|$ probability

 

p-value of the t value


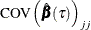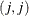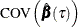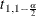Here $\mbox{COV}\left(\hat{\bbeta }(\tau )\right)_{jj}$ is the $(j,j)$ element of $\mbox{COV}\left(\hat{\bbeta }(\tau )\right)$, and $t_{1,1-{\alpha \over 2}}$ denotes the 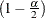$\left(1-{\alpha \over 2}\right)$-level student’s t score with 1 degree of freedom.