The HPQUANTSELECT Procedure

Linear-in-Parameter Model with Non-iid Settings

The general form of a linear quantile regression model is

$Q_ Y(\tau |\mb{x})=\mb{x}’\bbeta (\tau )$

where the iid assumption is not necessary. Under some regularity conditions, the asymptotic distribution of the general form of quantile regression estimates is

$\sqrt {n}({\hat\bbeta }(\tau ) - \bbeta (\tau )) \rightarrow N(0,\tau (1-\tau )\mb{H}_ n^{-}\bOmega \mb{H}_ n^{-})$

where $\mb{H}_ n=\lim _{n\rightarrow \infty } n^{-1}\sum \mb{x}_ i\mb{x}_ i^{\prime }f_ i(F_ i^{-1}(\tau )).$

Accordingly, the covariance matrix of 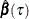${\hat\bbeta }(\tau )$ can be estimated as

$\hat{\Sigma }(\tau )=n^{-2}\tau (1-\tau ){\hat{\mb{H}}_ n^{-}}(\mb{X}’\mb{X}){\hat{\mb{H}}_ n^{-}}$

where $\hat{\mb{H}}_ n = n^{-1}\sum \left(\mb{x}_ i\mb{x}_ i^{\prime }/\hat{s}_ i(\tau )\right)$ .

The sparsity function of the ith observation, $\hat{s}_ i(\tau )$ , can be estimated as

$\hat{s}_ i(\tau )={{\hat{F}_ i^{-1}(\tau +h_ n)-\hat{F}_ i^{-1}(\tau -h_ n)} \over {2h_ n}}$

where $\hat{F}_ i^{-1}(\tau \pm h_ n)=\mb{x}_ i’\hat{\bbeta }(\tau \pm h_ n)$ are the ith predicted quantile values at quantile levels $(\tau \pm h_ n)$ .