The HPQUANTSELECT Procedure

Linear Model with iid Errors

You can specify the SPARSITY(IID) option in the MODEL statement to assume that the distribution of 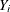$Y_ i$ conditional on $\mb{x}_ i$ follows the linear model

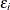\[ Y_ i = \mb{x}_ i^{\prime }\bbeta + \epsilon _ i \]

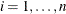where $\epsilon _ i$ for $i=1,\ldots ,n$ are iid in the distribution function F. Let 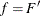$f=F^{\prime }$ denote the density function of F. Further assume that 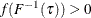$f(F^{-1}(\tau )) > 0$ in a neighborhood of $\tau $. Then, under some mild conditions, Koenker and Bassett (1982) prove that the asymptotic distribution of the quantile regression estimates is

\[ \sqrt {n}({\hat\bbeta }(\tau ) - \bbeta (\tau )) \rightarrow N(0, \omega ^2(\tau , F) \bOmega ^{-1}) \]

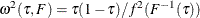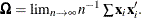where $\omega ^2(\tau , F) = \tau (1-\tau )\slash f^2(F^{-1}(\tau ))$ and $\bOmega =\lim _{n\rightarrow \infty } n^{-1}\sum \mb{x}_ i\mb{x}_ i^{\prime }.$ The reciprocal of the density function, 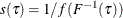$s(\tau )={1/ f(F^{-1}(\tau ))}$, is called the sparsity function.

Accordingly, the covariance matrix of 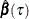${\hat\bbeta }(\tau )$ can be estimated as

\[ \hat{\Sigma }(\tau )=\tau (1-\tau )\hat{s}^2(\tau )(\mb{X}’\mb{X})^{-} \]

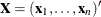where $\mb{X}=(\mb{x}_1,\ldots ,\mb{x}_ n)’$ is the design matrix and 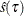$\hat{s}(\tau )$ is an estimate of 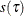$s(\tau )$. Under the iid assumption, the algorithm for computing 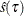$\hat{s}(\tau )$ is as follows:

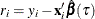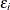  1. Fit a quantile regression model and compute the residuals. Each residual $r_ i=y_ i-\mb{x}_ i’\hat{\bbeta }(\tau )$ can be viewed as an estimated realization of the corresponding error $\epsilon _ i$.

  2. Compute the quantile level bandwidth 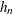$h_ n$. The HPQUANTSELECT procedure provides two bandwidth methods:

    • The Bofinger bandwidth is an optimizer of mean squared error for standard density estimation:

      \[ h_ n = n^{-1\slash 5} ( {4.5v^2(\tau )} )^{1\slash 5} \]

    • The Hall-Sheather bandwidth is based on Edgeworth expansions for studentized quantiles,

      \[ h_ n = n^{-1\slash 3} z_\alpha ^{2\slash 3} ( {1.5 v(\tau )} )^{1\slash 3} \]

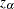      $z_\alpha $ satisfies 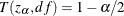$T(z_\alpha ,df) = 1- \alpha \slash 2$ for the construction of 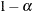$1-\alpha $ confidence intervals, where T is the cumulative distribution function for the t distribution and 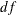$df$ is the residual degrees of freedom.

    The quantity

    \[ v(\tau ) = {\frac{s(\tau )}{s^{(2)}(\tau )}} = {\frac{f^2}{2(f^{(1)} \slash f)^2 + [(f^{(1)} \slash f)^2 - f^{(2)}\slash f ] }} \]

    is not sensitive to f and can be estimated by assuming f is Gaussian as

    \[ \hat{v}(\tau )={{\exp (-q^2)} \over 2\pi (q^2+1)} \]

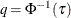    where $q=\Phi ^{-1}(\tau )$.

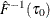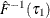  3. Compute residual quantiles $\hat{F}^{-1}(\tau _0)$ and $\hat{F}^{-1}(\tau _1)$ as follows:

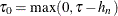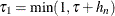    1. Set $\tau _0=\max (0,\tau -h_ n)$ and $\tau _1=\min (1,\tau +h_ n)$.

    2. Use the equation

      \[ {\hat F}^{-1}(t) = \left\{ \begin{array}{ll} r_{(1)} & {\mbox{if }} t\in [0, 1\slash 2n) \\ \lambda r_{(i+1)} + (1-\lambda ) r_{(i)} & {\mbox{if }} t\in [(i-0.5)\slash n, (i+0.5)\slash n) \\ r_{(n)} & {\mbox{if }} t\in [(2n-1), 1] \\ \end{array} \right. \]

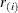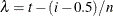      where $r_{(i)}$ is the ith smallest residual and $\lambda =t-(i-0.5)\slash n$.

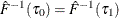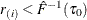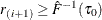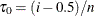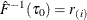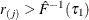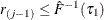    3. If ${\hat F}^{-1}(\tau _0)={\hat F}^{-1}(\tau _1)$, find i that satisfies $r_{(i)}<{\hat F}^{-1}(\tau _0)$ and $r_{(i+1)}\ge {\hat F}^{-1}(\tau _0)$. If such an i exists, reset $\tau _0=(i-0.5)/n$ so that ${\hat F}^{-1}(\tau _0)=r_{(i)}$. Also find j that satisfies $r_{(j)}>{\hat F}^{-1}(\tau _1)$ and $r_{(j-1)}\le {\hat F}^{-1}(\tau _1)$. 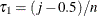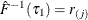If such a j exists, reset $\tau _1=(j-0.5)/n$ so that ${\hat F}^{-1}(\tau _1)=r_{(j)}$.

  4. Estimate the sparsity function 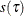$s(\tau )$ as

    \[ \hat{s}(\tau )={{\hat{F}^{-1}(\tau _1)-\hat{F}^{-1}(\tau _0)} \over {\tau _1-\tau _0}} \]