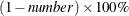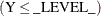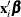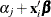The GEE Procedure

OUTPUT Statement

  • OUTPUT <OUT=SAS-data-set> <keyword=name …keyword=name>;

The OUTPUT statement creates a new SAS data set that contains all the variables in the input data set and, optionally, the estimated linear predictors (XBETA) and their standard error estimates, predicted values of the mean, and confidence limits for predicted values.

If you use the multinomial distribution with one of the cumulative link functions for ordinal data, the data set also contains variables named _ORDER_ and _LEVEL_ that indicate the levels of the ordinal response variable and the values of the variable in the input data set corresponding to the sorted levels. These variables indicate that the predicted value for a given observation is the probability that the response variable is as large as the value of the _LEVEL_ variable. Residuals and other diagnostic statistics are not available for the multinomial distribution.

The estimated linear predictor, its standard error estimate, and the predicted values and their confidence intervals are computed for all observations in which the explanatory variables are all nonmissing, even if the response is missing. By adding observations with missing response values to the input data set, you can compute these statistics for new observations or for settings of the explanatory variables not present in the data without affecting the model fit.

The following list explains specifications in the OUTPUT statement.

OUT=SAS-data-set

specifies the output data set. If you omit the OUT=option, the output data set is created and given a default name that uses the DATAn convention.

keyword=name

specifies the statistics to be included in the output data set and names the new variables that contain the statistics. Specify a keyword for each desired statistic (see the following list of keywords), an equal sign, and the name of the new variable or variables to contain the statistic.

Although you can use the OUTPUT statement without any keyword=name specifications, the output data set then contains only the original variables and, possibly, the variables Level and Value (if you use the multinomial model with ordinal data).

The keywords allowed and the statistics they represent are as follows:

LOWER | L

represents the lower confidence limit for the predicted value of the mean, or the lower confidence limit for the probability that the response is less than or equal to the value of Level or Value. The confidence coefficient is determined by the ALPHA=number option in the MODEL statement as 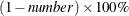$(1 - \mathit{number})\times 100\% $. The default confidence coefficient is 95%.

PREDICTED | PRED | PROB | P

represents the predicted value of the mean of the response or the predicted probability that the response variable is less than or equal to the value of _LEVEL_ if the multinomial model for ordinal data is used (in other words, Pr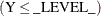$(\mr{Y} \le \mr{\_ LEVEL\_ })$, where Y is the response variable).

RESCHI

represents the Pearson (chi) residual for identifying observations that are poorly accounted for by the model. This option is not available for the multinomial distribution.

RESRAW

represents the raw residual for identifying poorly fitted observations. This option is not available for the multinomial distribution.

STDXBETA

represents the standard error estimate of XBETA (see the XBETA keyword).

UPPER | U

represents the upper confidence limit for the predicted value of the mean, or the upper confidence limit for the probability that the response is less than or equal to the value of Level or Value. The confidence coefficient is determined by the ALPHA=number option in the MODEL statement as 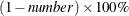$(1 - \mathit{number})\times 100\% $. The default confidence coefficient is 95%.

XBETA

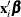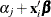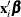represents the estimate of the linear predictor $\mb{x}_ i^\prime \bbeta $ for observation i, or ${\alpha }_ j+\mb{x}_ i^\prime \bbeta $, where j is the corresponding ordered value of the response variable for the multinomial model with ordinal data. If there is an offset, it is included in $\mb{x}_ i^\prime \bbeta $.