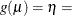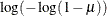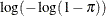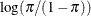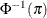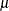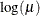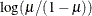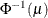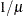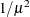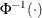The GEE Procedure

MODEL Statement

MODEL response = <effects> </ options>;

MODEL events/trials = <effects> </ options>;

The MODEL statement specifies the response (dependent variable) and the effects (explanatory variables). If you omit the explanatory variables, PROC GEE fits an intercept-only model. An intercept term is included in the model by default. You can remove the intercept by specifying the NOINT option.

You can specify the response in the form of a single variable (response) or in the form of a ratio of two variables ( events/trials). The first form is applicable to all responses. The second form is applicable only to summarized binomial response data. When each observation in the input data set contains the number of events (for example, successes) and the number of trials from a set of binomial trials, use the events/trials syntax.

In the events/trials model syntax, you specify two variables: one for the event counts and one for trial counts. These two variables are separated by a slash (/). The value of the events variable must be nonnegative, and the value of the trials variable must be equal to or greater than the value of the events variable for an observation to be valid. The events and trials variables can take non-integer values.

When each observation in the input data set contains a single trial from a binomial experiment, use the response form of the MODEL statement. The response variable can be numeric or character. The ordering of response levels is critical in these models.

Responses for the Poisson distribution must be all nonnegative, but they can be non-integer values.

The effects in the MODEL statement consist of an explanatory variable or combination of variables. Explanatory variables can be continuous or classification variables. Classification variables can be character or numeric. Explanatory variables that represent nominal (classification) data must be declared in a CLASS statement. Interactions between variables can also be included as effects. Columns of the design matrix are automatically generated for classification variables and interactions. The syntax for specifying effects is the same as for the GLM procedure. For more information, see the section Specification of Effects in Chapter 46: The GLM Procedure.

Table 43.5 summarizes the options available in the MODEL statement.

Table 43.5: MODEL Statement Options

Option	Description
ALPHA=	Sets the confidence coefficient
DIST=	Specifies the probability distribution
LINK=	Specifies the link function
NOINT	Requests no intercept term
NOSCALE	Holds the scale parameter fixed
OFFSET=	Specifies a variable in the input data set to be used as an offset
SCALE=	Specifies the value used for the scale

You can specify the following options after a slash (/).

ALPHA=number

sets the confidence coefficient for parameter confidence intervals to 1–number. The value of number must be between 0 and 1. The default value of number is 0.05.

DIST=keyword D=keyword ERROR=keyword ERR=keyword

specifies the built-in probability distribution to use in the model. If you specify the DIST= option and you omit the LINK= option, a default link function is chosen as displayed in Table 43.6. If you specify neither the DIST= option nor the LINK= option, then the GEE procedure defaults to the normal distribution with the identity link function.

Table 43.6: Distributions and Default Link Functions

DIST=	Distribution	Default Link Function
BINOMIAL \| BIN \| B	Binomial	Logit
GAMMA \| GAM \| G	Gamma	Reciprocal
IGAUSSIAN \| IG	Inverse Gaussian	Reciprocal square
MULTINOMIAL \| MULT	Multinomial	Cumulative logit
NEGBIN \| NB	Negative binomial	Log
NORMAL \| NOR \| N	Normal	Identity
POISSON \| POI \| P	Poisson	Log

LINK=keyword

specifies the link function in the model. You can specify the keywords shown in Table 43.7.

Table 43.7: Built-In Link Functions of the GEE Procedure

	Link
LINK=	Function	$g(\mu ) =\eta =$
CLOGLOG \| CLL	Complementary log-log	$\log (-\log (1-\mu ))$
CUMCLL \| CCLL	Cumulative complementary log-log	$\log (-\log (1-\pi ))$
CUMLOGIT\| CLOGIT	Cumulative logit	$\log (\pi /(1-\pi ))$
CUMPROBIT \| CPROBIT	Cumulative probit	$\Phi ^{-1}(\pi )$
GLOGIT	Generalized logit
IDENTITY \| ID	Identity	$\mu$
LOG	Log	$\log (\mu )$
LOGIT	Logit	$\log (\mu /(1-\mu ))$
PROBIT	Probit	$\Phi ^{-1}(\mu )$
INVERSE \| RECIPROCAL	Reciprocal	$1/\mu$
POWERMINUS2	Power with exponent –2	$1/\mu ^2$

For the probit and cumulative probit links, $\Phi ^{-1}(\cdot )$ denotes the quantile function of the standard normal distribution. If you do not specify the LINK= option, then by default the canonical link function is used if you specify the DIST= option. Otherwise, if you omit the DIST= option, the identity link function is used.

The cumulative link functions are appropriate only for the multinomial distribution with ordinal responses, with cumulative probabilities indicated by $\pi$ . The GLOGIT link function is appropriate only for the multinomial distribution with nominal responses.

NOINT

requests that no intercept term be included in the model. An intercept is included unless this option is specified.

NOSCALE

holds the scale parameter fixed. Otherwise, for the normal, inverse Gaussian, and gamma distributions, the scale parameter is estimated by maximum likelihood. If you omit the SCALE= option, the scale parameter is fixed at the value 1.

OFFSET=variable

specifies a variable in the input data set to be used as an offset variable. This variable cannot be a CLASS variable, the response variable, or any of the explanatory variables.

SCALE=number SCALE=PEARSON | P PSCALE SCALE=DEVIANCE | D DSCALE

specifies the value used for the scale parameter when the NOSCALE option is used. For the binomial and Poisson distributions, which have no free scale parameter, this can be used to specify an overdispersed model. If the NOSCALE option is not specified, then number is used as an initial estimate of the scale parameter.

Specifying SCALE=PEARSON or SCALE=P is the same as specifying the PSCALE option. This fixes the scale parameter at the value 1 in the estimation procedure. After the parameter estimates are determined, the exponential family dispersion parameter is assumed to be given by Pearson’s chi-square statistic divided by the degrees of freedom, and all statistics such as standard errors are adjusted appropriately.

Specifying SCALE=DEVIANCE or SCALE=D is the same as specifying the DSCALE option. This fixes the scale parameter at a value of 1 in the estimation procedure.