The GEE Procedure
Alternating Logistic Regression
If the responses are binary (that is, they take only two values), then there is an alternative method to account for the association
among the measurements. The alternating logistic regressions (ALR) algorithm of Carey, Zeger, and Diggle (1993) models the association between pairs of responses by using log odds ratios instead of using correlations, as ordinary GEEs
do. The ALR algorithm of Heagerty and Zeger (1996) extends the method to GEEs that have ordinal multinomial responses (that is, they fall into one of 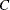 ordered categories).
ordered categories).
ALR for Binary Data
For binary data, the correlation between the jth and kth response is, by definition,
![\[ \mr{Corr}(Y_{ij},Y_{ik}) = \frac{\Pr (Y_{ij}=1,Y_{ik}=1)-\mu _{ij}\mu _{ik}}{\sqrt {\mu _{ij}(1-\mu _{ij})\mu _{ik}(1-\mu _{ik})}} \]](images/statug_gee0088.png)
The joint probability in the numerator satisfies the following bounds, by elementary properties of probability, because 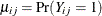 :
:
![\[ \max (0,\mu _{ij}+\mu _{ik}-1) \leq \Pr (Y_{ij}=1,Y_{ik}=1) \leq \min ( \mu _{ij},\mu _{ik}) \]](images/statug_gee0090.png)
Therefore, the correlation is constrained to be within limits that depend in a complicated way on the means of the data.
The odds ratio, defined as
![\[ \mr{OR}(Y_{ij},Y_{ik}) = \frac{\Pr (Y_{ij}=1,Y_{ik}=1)\Pr (Y_{ij}=0,Y_{ik}=0)}{\Pr (Y_{ij}=1,Y_{ik}=0)\Pr (Y_{ij}=0,Y_{ik}=1)} \]](images/statug_gee0091.png)
is not constrained by the means and is preferred, in some cases, to correlations for binary data.
The ALR algorithm seeks to model the logarithm of the odds ratio, 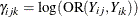 , as
, as
![\[ \gamma _{ijk} = \mb{z}_{ijk}’\balpha \]](images/statug_gee0093.png)
where  is a
is a 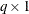 vector of regression parameters and
vector of regression parameters and 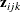 is a fixed, specified vector of coefficients.
is a fixed, specified vector of coefficients.
The parameter 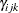 can take any value in
can take any value in 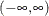 , with
, with 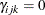 corresponding to no association.
corresponding to no association.
The log odds ratio, when modeled in this way with a regression model, can take different values in subgroups defined by 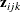 . For example,
. For example, 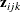 can define subgroups within clusters, or it can define "block effects" between clusters.
can define subgroups within clusters, or it can define "block effects" between clusters.
You specify a GEE model for binary data that uses log odds ratios by specifying a model for the mean, as in ordinary GEEs, and by specifying a model for the log odds ratios. You can use any of the link functions appropriate for binary data in the model for the mean, such as logistic, probit, or complementary log-log.
ALR for Ordinal Multinomial Data
For ordinal multinomial data, let 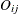 ,
, 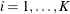 ,
, 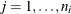 , denote the jth measurement on the ith subject. To apply the ALR algorithm, the responses
, denote the jth measurement on the ith subject. To apply the ALR algorithm, the responses 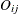 are represented by a vector
are represented by a vector ![$\mb{Y}_{ij}=\left[Y_{ij1},\dots ,Y_{ijC-1}\right]’$](images/statug_gee0102.png) of cumulative indicator variables
of cumulative indicator variables 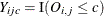 . You model the cumulative probabilities
. You model the cumulative probabilities 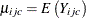 by using a cumulative link function,
by using a cumulative link function,
![\[ g\left( \mu _{ijc} \right)= \bbeta _ c +\mb{x}’_{ij}\bbeta , \mbox{ for } c=1,\dots ,C-1 \]](images/statug_gee0105.png)
where 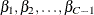 are increasing intercept terms that depend only on the level c. Let the binary vector that represents the responses of the ith subject be
are increasing intercept terms that depend only on the level c. Let the binary vector that represents the responses of the ith subject be ![$\mb{Y}_ i=\left[\mb{Y}_{i1},\dots ,\mb{Y}_{in_ i}\right]’$](images/statug_gee0107.png) with corresponding means
with corresponding means ![$\bmu _ i=\left[\mu _{i1},\dots ,\mu _{in_ i}\right]’$](images/statug_gee0108.png) .
.
The log odds ratio between two indicator variables 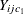 and
and 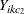 is modeled as
is modeled as
![\[ \gamma _{i(jk)(c_1c_2)}=\log (\mr{OR}(Y_{ijc_1},Y_{ikc_2}))=\mb{z}_{i(jk)(c_1c_2)}’\balpha \]](images/statug_gee0111.png)
for 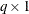 regression parameters
regression parameters  and fixed coefficients
and fixed coefficients 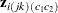 . As in Carey, Zeger, and Diggle (1993),
. As in Carey, Zeger, and Diggle (1993),  then provides a vector of regression parameters in a logistic model for the conditional expectation
then provides a vector of regression parameters in a logistic model for the conditional expectation 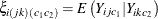 . To estimate
. To estimate  , the conditional expectation is considered for all pairs
, the conditional expectation is considered for all pairs 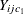 and
and 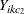 with
with 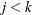 . Let
. Let
![\[ \begin{array}{l} \bxi _{i(jk)}=\left[\xi _{i(jk)(11)},\xi _{i(jk)(12)},\dots ,\xi _{i(jk)(21)},\dots ,\xi _{i(jk)(C-1,C-1)}\right]’ \vspace{2mm} \\ \bxi _{i}=\left[\bxi _{i(12)},\bxi _{i(13)},\dots ,\bxi _{i(23)},\dots ,\bxi _{i(n_ i-1n_ i)} \right]’ \vspace{2mm} \\ \mb{Y}^*_ i=\Big[ \overbrace{Y_{i1} \otimes e_{C-1},\dots ,Y_{i1} \otimes e_{C-1}}^\text {$n_ i-1$},\underbrace{Y_{i2} \otimes e_{C-1},\dots ,Y_{i2} \otimes e_{C-1}}_\text {$n_ i-2$},\dots ,\overbrace{Y_{in_ i-1} \otimes e_{C-1}}^\text {1} \Big]’ \end{array} \]](images/statug_gee0115.png)
where 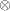 denotes the Kronecker product and
denotes the Kronecker product and 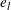 denotes a vector of dimension l composed of ones. The difference
denotes a vector of dimension l composed of ones. The difference 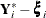 represents the residuals of the model for the conditional expectation.
represents the residuals of the model for the conditional expectation.
For both binary and multinomial data, the ALR estimates for 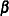 and
and  are the simultaneous solutions to the estimating equations
are the simultaneous solutions to the estimating equations
![\[ \begin{array}{l} \mb{S}_1(\bbeta ,\balpha )=\sum \limits _{i=1}^ K \frac{\partial \bmu _ i}{\partial \bbeta }’ \mb{V}_{i11}^{-1}\left(\mb{Y}_ i-\bmu _ i(\bbeta )\right)=\mb{0}\\ \mb{S}_2(\bbeta ,\balpha )=\sum \limits _{i=1}^ K \frac{\partial \bxi _ i}{\partial \balpha }’\mb{V}_{i33}^{-1}\left(\mb{Y}^*_ i-\bxi _ i \right)=\mb{0} \end{array} \]](images/statug_gee0119.png)
where 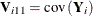 and
and ![$\mb{V}_{i33}=\mbox{diag}\left[\bxi _ i\left(1- \bxi _ i\right) \right]$](images/statug_gee0121.png) . The fitting algorithm alternates between a GEE step to update the model for the mean and a logistic regression step to update
the log odds ratio model. Upon convergence, the ALR algorithm provides estimates of the regression parameters for the mean,
. The fitting algorithm alternates between a GEE step to update the model for the mean and a logistic regression step to update
the log odds ratio model. Upon convergence, the ALR algorithm provides estimates of the regression parameters for the mean,
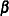 ; the regression parameters for the log odds ratios,
; the regression parameters for the log odds ratios,  ; their standard errors; and their covariances.
; their standard errors; and their covariances.
Specifying Log Odds Ratio Models
Specifying a regression model for the log odds ratio requires you to specify the rows of the matrix  . For binary data, there is a row
. For binary data, there is a row 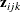 for each cluster i and within-cluster pair
for each cluster i and within-cluster pair 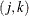 . For ordinal multinomial data, there is a row
. For ordinal multinomial data, there is a row 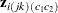 for each cluster i, within-cluster pair
for each cluster i, within-cluster pair 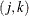 , and choice of levels
, and choice of levels 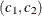 .
.
For ordinal multinomial data, the GEE procedure supports only the ALR method that uses a fully exchangeable regression structure
for the log odds ratio. In a fully exchangeable model, the log odds ratio is constant for all clusters i, within-cluster pair 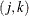 , and levels
, and levels 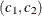 . You select a fully exchangeable model for the log odds ratio by specifying LOGOR=EXCH.
. You select a fully exchangeable model for the log odds ratio by specifying LOGOR=EXCH.
For binary data, the GEE procedure provides several methods of specifying 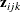 . You apply these methods by specifying LOGOR=keyword and associated options in the REPEATED statement. The supported keywords and the resulting log odds ratio models are described as follows:
. You apply these methods by specifying LOGOR=keyword and associated options in the REPEATED statement. The supported keywords and the resulting log odds ratio models are described as follows:
- EXCH
-
specifies exchangeable log odds ratios. In this model, the log odds ratio is a constant for all clusters i and pairs
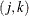 . The parameter
. The parameter  is the common log odds ratio.
is the common log odds ratio.
![\[ \mb{z}_{ijk} = 1 \; \; \mbox{ for all } \; \; i, j, k \]](images/statug_gee0124.png)
- FULLCLUST
-
specifies fully parameterized clusters. Each cluster is parameterized in the same way, and there is a parameter for each unique pair within clusters. If a complete cluster is of size n, then there are
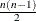 parameters in the vector
parameters in the vector  . For example, if a full cluster is of size 4, then there are
. For example, if a full cluster is of size 4, then there are 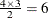 parameters, and the
parameters, and the  matrix is of the form
matrix is of the form
![\[ \bZ = \left[ \begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right] \]](images/statug_gee0127.png)
The elements of
 correspond to log odds ratios for cluster pairs in the following order:
correspond to log odds ratios for cluster pairs in the following order:
|
Pair |
Parameter |
|---|---|
|
(1,2) |
Alpha1 |
|
(1,3) |
Alpha2 |
|
(1,4) |
Alpha3 |
|
(2.3) |
Alpha4 |
|
(2,4) |
Alpha5 |
|
(3,4) |
Alpha6 |
- LOGORVAR(variable)
-
specifies log odds ratios by cluster. The argument variable is a variable name that defines the "block effects" between clusters. The log odds ratios are constant within clusters, but they take a different value for each different value of the variable. For example, if
Centeris a variable in the input data set that takes a different value for k treatment centers, then when you specify LOGOR=LOGORVAR(Center), you get a model that has different log odds ratios for each of the k centers, constant within center. - NESTK
-
specifies k-nested log odds ratios. You must also specify the SUBCLUST=variable option to define subclusters within clusters. Within each cluster, PROC GEE computes a log odds ratio parameter for pairs that have the same value of variable for both members of the pair and one log odds ratio parameter for each unique combination of different values of variable.
- NEST1
-
specifies 1-nested log odds ratios. You must also specify the SUBCLUST=variable option to define subclusters within clusters. There are two log odds ratio parameters for this model. Pairs that have the same value of variable correspond to one parameter; pairs that have different values of variable correspond to the other parameter. For example, if patients are clustered by hospital and subclusters are the wards within those hospitals, then the outcomes of patients within the same ward have one log odds ratio parameter, and the outcomes of patients from different wards have the other parameter.
- ZFULL
-
specifies the full
 matrix. You must also specify a SAS data set that contains the
matrix. You must also specify a SAS data set that contains the  matrix by using the ZDATA=data-set-name option. Each observation in the data set corresponds to one row of the
matrix by using the ZDATA=data-set-name option. Each observation in the data set corresponds to one row of the  matrix. You must specify the ZDATA data set as if all clusters are complete—that is, as if all clusters are the same size
and there are no missing observations. The ZDATA data set has
matrix. You must specify the ZDATA data set as if all clusters are complete—that is, as if all clusters are the same size
and there are no missing observations. The ZDATA data set has ![$K [n_{\mathit{max}}(n_{\mathit{max}}-1)/2]$](images/statug_gee0128.png) observations, where K is the number of clusters and
observations, where K is the number of clusters and 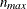 is the maximum cluster size. If the members of cluster i are ordered as
is the maximum cluster size. If the members of cluster i are ordered as 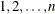 , then the rows of the
, then the rows of the  matrix must be specified for pairs in the order
matrix must be specified for pairs in the order 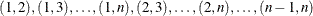 . The variables that you specify in the REPEATED statement for the SUBJECT effect must also be present in the ZDATA= data
set to identify clusters. You must specify variables in the data set that define the columns of the
. The variables that you specify in the REPEATED statement for the SUBJECT effect must also be present in the ZDATA= data
set to identify clusters. You must specify variables in the data set that define the columns of the  matrix by using the ZROW=variable-list option. If there are q columns (q variables in variable-list), then there are q log odds ratio parameters. You can optionally specify variables that indicate the cluster pairs corresponding to each row
of the
matrix by using the ZROW=variable-list option. If there are q columns (q variables in variable-list), then there are q log odds ratio parameters. You can optionally specify variables that indicate the cluster pairs corresponding to each row
of the  matrix by using the YPAIR=(variable1, variable2) option. If you specify this option, the data from the ZDATA data set are sorted within each cluster by variable1 and variable2. See Example 43.4 for an example of specifying a full
matrix by using the YPAIR=(variable1, variable2) option. If you specify this option, the data from the ZDATA data set are sorted within each cluster by variable1 and variable2. See Example 43.4 for an example of specifying a full  matrix.
matrix.
- ZREP
-
specifies a replicated
 matrix. You specify
matrix. You specify  matrix data exactly as you do for the ZFULL option case, except that you specify only one complete cluster. The
matrix data exactly as you do for the ZFULL option case, except that you specify only one complete cluster. The  matrix for the one cluster is replicated for each cluster. The number of observations in the ZDATA data set is
matrix for the one cluster is replicated for each cluster. The number of observations in the ZDATA data set is 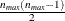 , where
, where 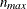 is the size of a complete cluster (a cluster with no missing observations).
is the size of a complete cluster (a cluster with no missing observations).
- ZREP(matrix)
-
specifies direct input of the replicated
 matrix. You specify the
matrix. You specify the  matrix for one cluster by using the syntax LOGOR=ZREP (
matrix for one cluster by using the syntax LOGOR=ZREP ( 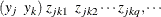 ), where
), where 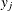 and
and 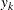 are numbers that represent a pair of observations from the ith cluster and the values
are numbers that represent a pair of observations from the ith cluster and the values 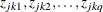 make up the corresponding row
make up the corresponding row 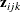 of the
of the  matrix. The number of specified rows is
matrix. The number of specified rows is 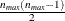 , where
, where 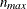 is the size of a complete cluster (a cluster with no missing observations). For example,
is the size of a complete cluster (a cluster with no missing observations). For example,
logor = zrep((1 2) 1 0, (1 3) 1 0, (1 4) 1 0, (2 3) 1 1, (2 4) 1 1, (3 4) 1 1)specifies the
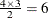 rows of the
rows of the  matrix for a cluster of size 4 with q = 2 log odds ratio parameters. The log odds ratio for the pairs (1 2), (1 3), (1 4) is
matrix for a cluster of size 4 with q = 2 log odds ratio parameters. The log odds ratio for the pairs (1 2), (1 3), (1 4) is 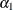 , and the log odds ratio for the pairs (2 3), (2 4), (3 4) is
, and the log odds ratio for the pairs (2 3), (2 4), (3 4) is 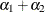 .
.
