The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression - References
This example illustrates the use of cumulative residuals to assess the adequacy of a normal linear regression model. Neter et al. (1996, Section 8.2) describe a study of 54 patients undergoing a certain kind of liver operation in a surgical unit. The data consist of the survival time and certain covariates. After a model selection procedure, they arrived at the following model:
where Y is the logarithm (base 10) of the survival time; ![]() ,
, ![]() ,
, ![]() are blood-clotting score, prognostic index, and enzyme function, respectively; and
are blood-clotting score, prognostic index, and enzyme function, respectively; and ![]() is a normal error term. A listing of the SAS data set containing the data is shown in Output 42.8.1. The variables
is a normal error term. A listing of the SAS data set containing the data is shown in Output 42.8.1. The variables Y, X1, X2, and X3 correspond to Y, ![]() ,
, ![]() , and
, and ![]() , and
, and LogX1 is log(![]() ). The PROC GENMOD fit of the model is shown in Output 42.8.2. The analysis first focuses on the adequacy of the functional form of
). The PROC GENMOD fit of the model is shown in Output 42.8.2. The analysis first focuses on the adequacy of the functional form of ![]() , blood-clotting score.
, blood-clotting score.
Output 42.8.1: Surgical Unit Example Data
| Obs | Y | X1 | X2 | X3 | LogX1 |
|---|---|---|---|---|---|
| 1 | 2.3010 | 6.7 | 62 | 81 | 0.82607 |
| 2 | 2.0043 | 5.1 | 59 | 66 | 0.70757 |
| 3 | 2.3096 | 7.4 | 57 | 83 | 0.86923 |
| 4 | 2.0043 | 6.5 | 73 | 41 | 0.81291 |
| 5 | 2.7067 | 7.8 | 65 | 115 | 0.89209 |
| 6 | 1.9031 | 5.8 | 38 | 72 | 0.76343 |
| 7 | 1.9031 | 5.7 | 46 | 63 | 0.75587 |
| 8 | 2.1038 | 3.7 | 68 | 81 | 0.56820 |
| 9 | 2.3054 | 6.0 | 67 | 93 | 0.77815 |
| 10 | 2.3075 | 3.7 | 76 | 94 | 0.56820 |
| 11 | 2.5172 | 6.3 | 84 | 83 | 0.79934 |
| 12 | 1.8129 | 6.7 | 51 | 43 | 0.82607 |
| 13 | 2.9191 | 5.8 | 96 | 114 | 0.76343 |
| 14 | 2.5185 | 5.8 | 83 | 88 | 0.76343 |
| 15 | 2.2253 | 7.7 | 62 | 67 | 0.88649 |
| 16 | 2.3365 | 7.4 | 74 | 68 | 0.86923 |
| 17 | 1.9395 | 6.0 | 85 | 28 | 0.77815 |
| 18 | 1.5315 | 3.7 | 51 | 41 | 0.56820 |
| 19 | 2.3324 | 7.3 | 68 | 74 | 0.86332 |
| 20 | 2.2355 | 5.6 | 57 | 87 | 0.74819 |
| 21 | 2.0374 | 5.2 | 52 | 76 | 0.71600 |
| 22 | 2.1335 | 3.4 | 83 | 53 | 0.53148 |
| 23 | 1.8451 | 6.7 | 26 | 68 | 0.82607 |
| 24 | 2.3424 | 5.8 | 67 | 86 | 0.76343 |
| 25 | 2.4409 | 6.3 | 59 | 100 | 0.79934 |
| 26 | 2.1584 | 5.8 | 61 | 73 | 0.76343 |
| 27 | 2.2577 | 5.2 | 52 | 86 | 0.71600 |
| 28 | 2.7589 | 11.2 | 76 | 90 | 1.04922 |
| 29 | 1.8573 | 5.2 | 54 | 56 | 0.71600 |
| 30 | 2.2504 | 5.8 | 76 | 59 | 0.76343 |
| 31 | 1.8513 | 3.2 | 64 | 65 | 0.50515 |
| 32 | 1.7634 | 8.7 | 45 | 23 | 0.93952 |
| 33 | 2.0645 | 5.0 | 59 | 73 | 0.69897 |
| 34 | 2.4698 | 5.8 | 72 | 93 | 0.76343 |
| 35 | 2.0607 | 5.4 | 58 | 70 | 0.73239 |
| 36 | 2.2648 | 5.3 | 51 | 99 | 0.72428 |
| 37 | 2.0719 | 2.6 | 74 | 86 | 0.41497 |
| 38 | 2.0792 | 4.3 | 8 | 119 | 0.63347 |
| 39 | 2.1790 | 4.8 | 61 | 76 | 0.68124 |
| 40 | 2.1703 | 5.4 | 52 | 88 | 0.73239 |
| 41 | 1.9777 | 5.2 | 49 | 72 | 0.71600 |
| 42 | 1.8751 | 3.6 | 28 | 99 | 0.55630 |
| 43 | 2.6840 | 8.8 | 86 | 88 | 0.94448 |
| 44 | 2.1847 | 6.5 | 56 | 77 | 0.81291 |
| 45 | 2.2810 | 3.4 | 77 | 93 | 0.53148 |
| 46 | 2.0899 | 6.5 | 40 | 84 | 0.81291 |
| 47 | 2.4928 | 4.5 | 73 | 106 | 0.65321 |
| 48 | 2.5999 | 4.8 | 86 | 101 | 0.68124 |
| 49 | 2.1987 | 5.1 | 67 | 77 | 0.70757 |
| 50 | 2.4914 | 3.9 | 82 | 103 | 0.59106 |
| 51 | 2.0934 | 6.6 | 77 | 46 | 0.81954 |
| 52 | 2.0969 | 6.4 | 85 | 40 | 0.80618 |
| 53 | 2.2967 | 6.4 | 59 | 85 | 0.80618 |
| 54 | 2.4955 | 8.8 | 78 | 72 | 0.94448 |
In order to assess the adequacy of the fitted multiple regression model, the ASSESS statement in the following SAS statements
is used to create the plots of cumulative residuals against X1 shown in Output 42.8.3 and Output 42.8.4 and the summary table in Output 42.8.5:
ods graphics on;
proc genmod data=Surg;
model Y = X1 X2 X3 / scale=Pearson;
assess var=(X1) / resample=10000
seed=603708000
crpanel;
run;
Output 42.8.2: Regression Model for Linear X1
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |
| Intercept | 1 | 0.4836 | 0.0426 | 0.4001 | 0.5672 | 128.71 | <.0001 |
| X1 | 1 | 0.0692 | 0.0041 | 0.0612 | 0.0772 | 288.17 | <.0001 |
| X2 | 1 | 0.0093 | 0.0004 | 0.0085 | 0.0100 | 590.45 | <.0001 |
| X3 | 1 | 0.0095 | 0.0003 | 0.0089 | 0.0101 | 966.07 | <.0001 |
| Scale | 0 | 0.0469 | 0.0000 | 0.0469 | 0.0469 | ||
| Note: | The scale parameter was estimated by the square root of Pearson's Chi-Square/DOF. |
See Lin, Wei, and Ying (2002) for details about model assessment that uses cumulative residual plots. The RESAMPLE= keyword specifies that a p-value be computed based on a sample of 10,000 simulated residual paths. A random number seed is specified by the SEED= keyword for reproducibility. If you do not specify the seed, one is derived from the time of day. The keyword CRPANEL specifies that the panel of four cumulative residual plots shown in Output 42.8.4 be created, each with two simulated paths. The single residual plot with 20 simulated paths in Output 42.8.3 is created by default.
To request these graphs, ODS Graphics must be enabled and you must specify the ASSESS statement. For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS. For specific information about the graphics available in the GENMOD procedure, see the section ODS Graphics.
Output 42.8.5: Summary of Model Assessment
| Assessment Summary | ||||
|---|---|---|---|---|
| Assessment Variable |
Maximum Absolute Value |
Replications | Seed | Pr > MaxAbsVal |
| X1 | 0.0380 | 10000 | 603708000 | 0.1084 |
The p-value of 0.1084 reported on Output 42.8.3 and Output 42.8.5 suggests that a more adequate model might be possible. The observed cumulative residuals in Output 42.8.3 and Output 42.8.4, represented by the heavy lines, seem atypical of the simulated curves, represented by the light lines, reinforcing the conclusion
that a more appropriate functional form for X1 is possible.
The cumulative residual plots in Output 42.8.6 provide guidance in determining a more appropriate functional form. The four curves were created from simple forms of model misspecification by using simulated data. The mean models of the data and the fitted model are shown in Table 42.19.
The observed cumulative residual pattern in Output 42.8.3 and Output 42.8.4 most resembles the behavior of the curve in plot (a) of Output 42.8.6, indicating that log(![]() ) might be a more appropriate term in the model than
) might be a more appropriate term in the model than ![]() .
.
The following SAS statements fit a model with LogX1 in place of X1 and request a model assessment:
proc genmod data=Surg;
model Y = LogX1 X2 X3 / scale=Pearson;
assess var=(LogX1) / resample=10000
seed=603708000;
run;
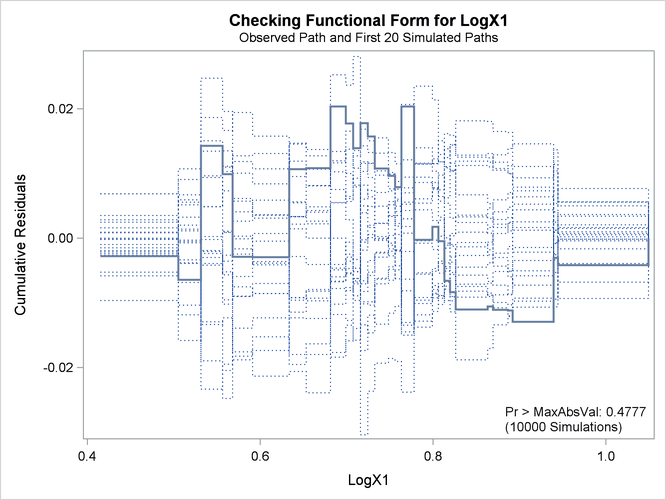
The revised model fit is shown in Output 42.8.7, the p-value from the simulation is 0.4777, and the cumulative residuals plotted in Output 42.8.8 show no systematic trend. The log transformation for X1 is more appropriate. Under the revised model, the p-values for testing the functional forms of X2 and X3 are 0.20 and 0.63, respectively; and the p-value for testing the linearity of the model is 0.65. Thus, the revised model seems reasonable.
Output 42.8.7: Multiple Regression Model with Log(X1)
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |
| Intercept | 1 | 0.1844 | 0.0504 | 0.0857 | 0.2832 | 13.41 | 0.0003 |
| LogX1 | 1 | 0.9121 | 0.0491 | 0.8158 | 1.0083 | 345.05 | <.0001 |
| X2 | 1 | 0.0095 | 0.0004 | 0.0088 | 0.0102 | 728.62 | <.0001 |
| X3 | 1 | 0.0096 | 0.0003 | 0.0090 | 0.0101 | 1139.73 | <.0001 |
| Scale | 0 | 0.0434 | 0.0000 | 0.0434 | 0.0434 | ||
| Note: | The scale parameter was estimated by the square root of Pearson's Chi-Square/DOF. |