The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG Statement ASSESS Statement BASELINE Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement ESTIMATE Statement FREQ Statement HAZARDRATIO Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements RANDOM Statement STRATA Statement SLICE Statement STORE Statement TEST Statement WEIGHT Statement
PROC PHREG Statement ASSESS Statement BASELINE Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement ESTIMATE Statement FREQ Statement HAZARDRATIO Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements RANDOM Statement STRATA Statement SLICE Statement STORE Statement TEST Statement WEIGHT Statement -
Details
 Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Counting Process Style of Input Left-Truncation of Failure Times The Multiplicative Hazards Model The Frailty Model Hazard Ratios Specifics for Classical Analysis Specifics for Bayesian Analysis Computational Resources Input and Output Data Sets Displayed Output ODS Table Names ODS Graphics
Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Counting Process Style of Input Left-Truncation of Failure Times The Multiplicative Hazards Model The Frailty Model Hazard Ratios Specifics for Classical Analysis Specifics for Bayesian Analysis Computational Resources Input and Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples
 Stepwise Regression Best Subset Selection Modeling with Categorical Predictors Firth’s Correction for Monotone Likelihood Conditional Logistic Regression for m:n Matching Model Using Time-Dependent Explanatory Variables Time-Dependent Repeated Measurements of a Covariate Survivor Function Estimates for Specific Covariate Values Analysis of Residuals Analysis of Recurrent Events Data Analysis of Clustered Data Model Assessment Using Cumulative Sums of Martingale Residuals Bayesian Analysis of the Cox Model Bayesian Analysis of Piecewise Exponential Model
Stepwise Regression Best Subset Selection Modeling with Categorical Predictors Firth’s Correction for Monotone Likelihood Conditional Logistic Regression for m:n Matching Model Using Time-Dependent Explanatory Variables Time-Dependent Repeated Measurements of a Covariate Survivor Function Estimates for Specific Covariate Values Analysis of Residuals Analysis of Recurrent Events Data Analysis of Clustered Data Model Assessment Using Cumulative Sums of Martingale Residuals Bayesian Analysis of the Cox Model Bayesian Analysis of Piecewise Exponential Model - References
Example 66.3 Modeling with Categorical Predictors
Consider the data for the Veterans Administration lung cancer trial presented in Appendix 1 of Kalbfleisch and Prentice (1980). In this trial, males with advanced inoperable lung cancer were randomized to a standard therapy and a test chemotherapy. The primary endpoint for the therapy comparison was time to death in days, represented by the variable Time. Negative values of Time are censored values. The data include information about a number of explanatory variables: Therapy (type of therapy: standard or test), Cell (type of tumor cell: adeno, large, small, or squamous), Prior (prior therapy: 0=no, 10=yes), Age (age, in years), Duration (months from diagnosis to randomization), and Kps (Karnofsky performance scale). A censoring indicator variable, Censor, is created from the data, with the value 1 indicating a censored time and the value 0 indicating an event time. The following DATA step saves the data in the data set VALung.
proc format;
value yesno 0='no' 10='yes';
run;
data VALung;
drop check m;
retain Therapy Cell;
infile cards column=column;
length Check $ 1;
label Time='time to death in days'
Kps='Karnofsky performance scale'
Duration='months from diagnosis to randomization'
Age='age in years'
Prior='prior therapy'
Cell='cell type'
Therapy='type of treatment';
format Prior yesno.;
M=Column;
input Check $ @@;
if M>Column then M=1;
if Check='s'|Check='t' then do;
input @M Therapy $ Cell $;
delete;
end;
else do;
input @M Time Kps Duration Age Prior @@;
Status=(Time>0);
Time=abs(Time);
end;
datalines;
standard squamous
72 60 7 69 0 411 70 5 64 10 228 60 3 38 0 126 60 9 63 10
118 70 11 65 10 10 20 5 49 0 82 40 10 69 10 110 80 29 68 0
314 50 18 43 0 -100 70 6 70 0 42 60 4 81 0 8 40 58 63 10
144 30 4 63 0 -25 80 9 52 10 11 70 11 48 10
standard small
30 60 3 61 0 384 60 9 42 0 4 40 2 35 0 54 80 4 63 10
13 60 4 56 0 -123 40 3 55 0 -97 60 5 67 0 153 60 14 63 10
59 30 2 65 0 117 80 3 46 0 16 30 4 53 10 151 50 12 69 0
22 60 4 68 0 56 80 12 43 10 21 40 2 55 10 18 20 15 42 0
139 80 2 64 0 20 30 5 65 0 31 75 3 65 0 52 70 2 55 0
287 60 25 66 10 18 30 4 60 0 51 60 1 67 0 122 80 28 53 0
27 60 8 62 0 54 70 1 67 0 7 50 7 72 0 63 50 11 48 0
392 40 4 68 0 10 40 23 67 10
standard adeno
8 20 19 61 10 92 70 10 60 0 35 40 6 62 0 117 80 2 38 0
132 80 5 50 0 12 50 4 63 10 162 80 5 64 0 3 30 3 43 0
95 80 4 34 0
standard large
177 50 16 66 10 162 80 5 62 0 216 50 15 52 0 553 70 2 47 0
278 60 12 63 0 12 40 12 68 10 260 80 5 45 0 200 80 12 41 10
156 70 2 66 0 -182 90 2 62 0 143 90 8 60 0 105 80 11 66 0
103 80 5 38 0 250 70 8 53 10 100 60 13 37 10
test squamous
999 90 12 54 10 112 80 6 60 0 -87 80 3 48 0 -231 50 8 52 10
242 50 1 70 0 991 70 7 50 10 111 70 3 62 0 1 20 21 65 10
587 60 3 58 0 389 90 2 62 0 33 30 6 64 0 25 20 36 63 0
357 70 13 58 0 467 90 2 64 0 201 80 28 52 10 1 50 7 35 0
30 70 11 63 0 44 60 13 70 10 283 90 2 51 0 15 50 13 40 10
test small
25 30 2 69 0 -103 70 22 36 10 21 20 4 71 0 13 30 2 62 0
87 60 2 60 0 2 40 36 44 10 20 30 9 54 10 7 20 11 66 0
24 60 8 49 0 99 70 3 72 0 8 80 2 68 0 99 85 4 62 0
61 70 2 71 0 25 70 2 70 0 95 70 1 61 0 80 50 17 71 0
51 30 87 59 10 29 40 8 67 0
test adeno
24 40 2 60 0 18 40 5 69 10 -83 99 3 57 0 31 80 3 39 0
51 60 5 62 0 90 60 22 50 10 52 60 3 43 0 73 60 3 70 0
8 50 5 66 0 36 70 8 61 0 48 10 4 81 0 7 40 4 58 0
140 70 3 63 0 186 90 3 60 0 84 80 4 62 10 19 50 10 42 0
45 40 3 69 0 80 40 4 63 0
test large
52 60 4 45 0 164 70 15 68 10 19 30 4 39 10 53 60 12 66 0
15 30 5 63 0 43 60 11 49 10 340 80 10 64 10 133 75 1 65 0
111 60 5 64 0 231 70 18 67 10 378 80 4 65 0 49 30 3 37 0
;
The following statements use the PHREG procedure to fit the Cox proportional hazards model to these data. The variables Prior, Cell, and Therapy, which are categorical variables, are declared in the CLASS statement. By default, PROC PHREG parameterizes the CLASS variables by using the reference coding with the last category as the reference category. However, you can explicitly specify the reference category of your choice. Here, Prior=no is chosen as the reference category for prior therapy, Cell=large is chosen as the reference category for type of tumor cell, and Therapy=standard is chosen as the reference category for the type of therapy. In the MODEL statement, the term Prior|Therapy is just another way of specifying the main effects Prior, Therapy, and the Prior*Therapy interaction.
proc phreg data=VALung; class Prior(ref='no') Cell(ref='large') Therapy(ref='standard'); model Time*Status(0) = Kps Duration Age Cell Prior|Therapy; run;
Coding of the CLASS variables is displayed in Output 66.3.1. There is one dummy variable for Prior and one for Therapy, since both variables are binary. The dummy variable has a value of 0 for the reference category (Prior=no, Therapy=standard). The variable Cell has four categories and is represented by three dummy variables. Note that the reference category, Cell=large, has a value of 0 for all three dummy variables.
| Class Level Information | ||||
|---|---|---|---|---|
| Class | Value | Design Variables | ||
| Prior | no | 0 | ||
| yes | 1 | |||
| Cell | adeno | 1 | 0 | 0 |
| large | 0 | 0 | 0 | |
| small | 0 | 1 | 0 | |
| squamous | 0 | 0 | 1 | |
| Therapy | standard | 0 | ||
| test | 1 | |||
The test results of individual model effects are shown in Output 66.3.2. There is a strong prognostic effect of Kps on patient’s survivivorship (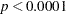 ), and the survival times for patients of different Cell types differ significantly (
), and the survival times for patients of different Cell types differ significantly (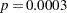 ). The Prior*Therapy interaction is marginally significant (p=0.0416)—that is, prior therapy might play a role in whether one treatment is more effective than the other.
). The Prior*Therapy interaction is marginally significant (p=0.0416)—that is, prior therapy might play a role in whether one treatment is more effective than the other.
| Type 3 Tests | |||
|---|---|---|---|
| Effect | DF | Wald Chi-Square | Pr > ChiSq |
| Kps | 1 | 35.5051 | <.0001 |
| Duration | 1 | 0.1159 | 0.7335 |
| Age | 1 | 1.9772 | 0.1597 |
| Cell | 3 | 18.5339 | 0.0003 |
| Prior | 1 | 2.5296 | 0.1117 |
| Therapy | 1 | 5.2349 | 0.0221 |
| Prior*Therapy | 1 | 4.1528 | 0.0416 |
In the Cox proportional hazards model, the effects of the covariates are to act multiplicatively on the hazard of the survival time, and therefore it is a little easier to interpret the corresponding hazard ratios than the regression parameters. For a parameter that corresponds to a continuous variable, the hazard ratio is the ratio of hazard rates for a increase of one unit of the variable. From Output 66.3.3, the hazard ratio estimate for Kps is 0.968, meaning that an increase of 10 units in Karnofsky performance scale will shrink the hazard rate by 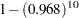 =28%. For a CLASS variable parameter, the hazard ratio presented in the Output 66.3.3 is the ratio of the hazard rates between the given category and the reference category. The hazard rate of Cell=adeno is 219% that of Cell=large, the hazard rate of Cell=small is 62% that of Cell=large, and the hazard rate of Cell=squamous is only 66% that of Cell=large. Hazard ratios for Prior and Therapy are missing since the model contains the Prior*Therapy interaction. You can use the HAZARDRATIO statement to obtain the hazard ratios for a main effect in the presence of interaction as shown later in this example.
=28%. For a CLASS variable parameter, the hazard ratio presented in the Output 66.3.3 is the ratio of the hazard rates between the given category and the reference category. The hazard rate of Cell=adeno is 219% that of Cell=large, the hazard rate of Cell=small is 62% that of Cell=large, and the hazard rate of Cell=squamous is only 66% that of Cell=large. Hazard ratios for Prior and Therapy are missing since the model contains the Prior*Therapy interaction. You can use the HAZARDRATIO statement to obtain the hazard ratios for a main effect in the presence of interaction as shown later in this example.
| Analysis of Maximum Likelihood Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Parameter Estimate |
Standard Error |
Chi-Square | Pr > ChiSq | Hazard Ratio |
Label | ||
| Kps | 1 | -0.03300 | 0.00554 | 35.5051 | <.0001 | 0.968 | Karnofsky performance scale | ||
| Duration | 1 | 0.00323 | 0.00949 | 0.1159 | 0.7335 | 1.003 | months from diagnosis to randomization | ||
| Age | 1 | -0.01353 | 0.00962 | 1.9772 | 0.1597 | 0.987 | age in years | ||
| Cell | adeno | 1 | 0.78356 | 0.30382 | 6.6512 | 0.0099 | 2.189 | cell type adeno | |
| Cell | small | 1 | 0.48230 | 0.26537 | 3.3032 | 0.0691 | 1.620 | cell type small | |
| Cell | squamous | 1 | -0.40770 | 0.28363 | 2.0663 | 0.1506 | 0.665 | cell type squamous | |
| Prior | yes | 1 | 0.45914 | 0.28868 | 2.5296 | 0.1117 | . | prior therapy yes | |
| Therapy | test | 1 | 0.56662 | 0.24765 | 5.2349 | 0.0221 | . | type of treatment test | |
| Prior*Therapy | yes | test | 1 | -0.87579 | 0.42976 | 4.1528 | 0.0416 | . | prior therapy yes * type of treatment test |
The following PROC PHREG statements illustrate the use of the backward elimination process to identify the effects that affect the survivorship of the lung cancer patients. The option SELECTION=BACKWARD is specified to carry out the backward elimination. The option SLSTAY=0.1 specifies the significant level for retaining the effects in the model.
proc phreg data=VALung;
class Prior(ref='no') Cell(ref='large') Therapy(ref='standard');
model Time*Status(0) = Kps Duration Age Cell Prior|Therapy
/ selection=backward slstay=0.1;
run;
Results of the backward elimination process are summarized in Output 66.3.4. The effect Duration was eliminated first and was followed by Age.
| Summary of Backward Elimination | ||||||
|---|---|---|---|---|---|---|
| Step | Effect Removed |
DF | Number In |
Wald Chi-Square |
Pr > ChiSq | Effect Label |
| 1 | Duration | 1 | 6 | 0.1159 | 0.7335 | months from diagnosis to randomization |
| 2 | Age | 1 | 5 | 2.0458 | 0.1526 | age in years |
Output 66.3.5 shows the Type 3 analysis of effects and the maximum likelihood estimates of the regression coefficients of the model. Without controlling for Age and Duration, KPS and Cell remain significant, but the Prior*Therapy interaction is less prominent than before (p=0.0871) though still significant at 0.1 level.
| Type 3 Tests | |||
|---|---|---|---|
| Effect | DF | Wald Chi-Square | Pr > ChiSq |
| Kps | 1 | 35.9218 | <.0001 |
| Cell | 3 | 17.4134 | 0.0006 |
| Prior | 1 | 2.3113 | 0.1284 |
| Therapy | 1 | 3.8030 | 0.0512 |
| Prior*Therapy | 1 | 2.9269 | 0.0871 |
| Analysis of Maximum Likelihood Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Parameter Estimate |
Standard Error |
Chi-Square | Pr > ChiSq | Hazard Ratio |
Label | ||
| Kps | 1 | -0.03111 | 0.00519 | 35.9218 | <.0001 | 0.969 | Karnofsky performance scale | ||
| Cell | adeno | 1 | 0.74907 | 0.30465 | 6.0457 | 0.0139 | 2.115 | cell type adeno | |
| Cell | small | 1 | 0.44265 | 0.26168 | 2.8614 | 0.0907 | 1.557 | cell type small | |
| Cell | squamous | 1 | -0.41145 | 0.28309 | 2.1125 | 0.1461 | 0.663 | cell type squamous | |
| Prior | yes | 1 | 0.41755 | 0.27465 | 2.3113 | 0.1284 | . | prior therapy yes | |
| Therapy | test | 1 | 0.45670 | 0.23419 | 3.8030 | 0.0512 | . | type of treatment test | |
| Prior*Therapy | yes | test | 1 | -0.69443 | 0.40590 | 2.9269 | 0.0871 | . | prior therapy yes * type of treatment test |
Finally, the following statements refit the previous model and computes hazard ratios at settings beyond those displayed in the "Analysis of Maximum Likelihood Estimates" table. You can use either the HAZARDRATIO statement or the CONTRAST statement to obtain hazard ratios. Using the CONTRAST statement to compute hazard ratios for CLASS variables can be a daunting task unless you are familiar with the parameterization schemes (see the section Parameterization of Model Effects of Chapter 19, Shared Concepts and Topics, for details), but you have control over which specific hazard ratios you want to compute. HAZARDRATIO statements, on the other hand, are designed specifically to provide hazard ratios. They are easy to use and you can also request both the Wald confidence limits and the profile-likelihood confidence limits; the latter is not available for the CONTRAST statements. Three HAZARDRATIO statements are specified; each has the CL=BOTH option to request both the Wald confidence limits and the profile-likelihood limits. The first HAZARDRATIO statement, labeled ’H1’, estimates the hazard ratio for an increase of 10 units in the KPS; the UNITS= option specifies the number of units increase. The second HAZARDRATIO statement, labeled ’H2’ computes the hazard ratios for comparing any pairs of tumor Cell types. The third HAZARDRATIO statement, labeled ’H3’, compares the test therapy with the standard therapy. The DIFF=REF option specifies that each nonreference category is compared to the reference category. The purpose of using DIFF=REF here is to ensure that the hazard ratio is comparing the test therapy to the standard therapy instead of the other way around. Three CONTRAST statements, labeled ’C1’, ’C2’, and ’C3’, parallel to the HAZARDRATIO statements ’H1’, ’H2’, and ’H3’, respectively, are specified. The ESTIMATE=EXP option specifies that the linear predictors be estimated in the exponential scale, which are precisely the hazard ratios.
proc phreg data=VALung;
class Prior(ref='no') Cell(ref='large') Therapy(ref='standard');
model Time*Status(0) = Kps Cell Prior|Therapy;
hazardratio 'H1' Kps / units=10 cl=both;
hazardratio 'H2' Cell / cl=both;
hazardratio 'H3' Therapy / diff=ref cl=both;
contrast 'C1' Kps 10 / estimate=exp;
contrast 'C2' cell 1 0 0, /* adeno vs large */
cell 1 -1 0, /* adeno vs small */
cell 1 0 -1, /* adeno vs squamous */
cell 0 -1 0, /* large vs small */
cell 0 0 -1, /* large vs Squamous */
cell 0 1 -1 /* small vs squamous */
/ estimate=exp;
contrast 'C3' Prior 0 Therapy 1 Prior*Therapy 0,
Prior 0 Therapy 1 Prior*Therapy 1 / estimate=exp;
run;
Output 66.3.6 displays the results of the three HAZARDRATIO statements in separate tables. Results of the three CONTRAST statements are shown in one table in Output 66.3.7. However, point estimates and the Wald confidence limits for the hazard ratio agree in between the two outputs.
| H1: Hazard Ratios for Kps | |||||
|---|---|---|---|---|---|
| Description | Point Estimate | 95% Wald Confidence Limits | 95% Profile Likelihood Confidence Limits |
||
| Kps Unit=10 | 0.733 | 0.662 | 0.811 | 0.662 | 0.811 |
| H2: Hazard Ratios for Cell | |||||
|---|---|---|---|---|---|
| Description | Point Estimate | 95% Wald Confidence Limits | 95% Profile Likelihood Confidence Limits |
||
| Cell adeno vs large | 2.115 | 1.164 | 3.843 | 1.162 | 3.855 |
| Cell adeno vs small | 1.359 | 0.798 | 2.312 | 0.791 | 2.301 |
| Cell adeno vs squamous | 3.192 | 1.773 | 5.746 | 1.770 | 5.768 |
| Cell large vs small | 0.642 | 0.385 | 1.073 | 0.380 | 1.065 |
| Cell large vs squamous | 1.509 | 0.866 | 2.628 | 0.863 | 2.634 |
| Cell small vs squamous | 2.349 | 1.387 | 3.980 | 1.399 | 4.030 |
| H3: Hazard Ratios for Therapy | |||||
|---|---|---|---|---|---|
| Description | Point Estimate | 95% Wald Confidence Limits | 95% Profile Likelihood Confidence Limits |
||
| Therapy test vs standard At Prior=no | 1.579 | 0.998 | 2.499 | 0.998 | 2.506 |
| Therapy test vs standard At Prior=yes | 0.788 | 0.396 | 1.568 | 0.390 | 1.560 |
| Contrast Estimation and Testing Results by Row | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Contrast | Type | Row | Estimate | Standard Error |
Alpha | Confidence Limits | Wald Chi-Square |
Pr > ChiSq | |
| C1 | EXP | 1 | 0.7326 | 0.0380 | 0.05 | 0.6618 | 0.8111 | 35.9218 | <.0001 |
| C2 | EXP | 1 | 2.1150 | 0.6443 | 0.05 | 1.1641 | 3.8427 | 6.0457 | 0.0139 |
| C2 | EXP | 2 | 1.3586 | 0.3686 | 0.05 | 0.7982 | 2.3122 | 1.2755 | 0.2587 |
| C2 | EXP | 3 | 3.1916 | 0.9575 | 0.05 | 1.7727 | 5.7462 | 14.9629 | 0.0001 |
| C2 | EXP | 4 | 0.6423 | 0.1681 | 0.05 | 0.3846 | 1.0728 | 2.8614 | 0.0907 |
| C2 | EXP | 5 | 1.5090 | 0.4272 | 0.05 | 0.8664 | 2.6282 | 2.1125 | 0.1461 |
| C2 | EXP | 6 | 2.3493 | 0.6318 | 0.05 | 1.3868 | 3.9797 | 10.0858 | 0.0015 |
| C3 | EXP | 1 | 1.5789 | 0.3698 | 0.05 | 0.9977 | 2.4985 | 3.8030 | 0.0512 |
| C3 | EXP | 2 | 0.7884 | 0.2766 | 0.05 | 0.3964 | 1.5680 | 0.4593 | 0.4980 |