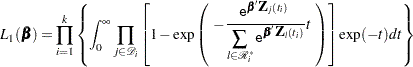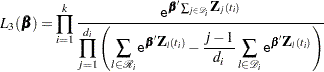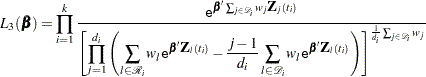The PHREG Procedure
- Overview
-
Getting Started
-
Syntax
PROC PHREG Statement ASSESS Statement BASELINE Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement ESTIMATE Statement FREQ Statement HAZARDRATIO Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements RANDOM Statement STRATA Statement SLICE Statement STORE Statement TEST Statement WEIGHT Statement
-
Details
Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Counting Process Style of Input Left-Truncation of Failure Times The Multiplicative Hazards Model The Frailty Model Hazard Ratios Specifics for Classical Analysis Specifics for Bayesian Analysis Computational Resources Input and Output Data Sets Displayed Output ODS Table Names ODS Graphics
-
Examples
Stepwise Regression Best Subset Selection Modeling with Categorical Predictors Firth’s Correction for Monotone Likelihood Conditional Logistic Regression for m:n Matching Model Using Time-Dependent Explanatory Variables Time-Dependent Repeated Measurements of a Covariate Survivor Function Estimates for Specific Covariate Values Analysis of Residuals Analysis of Recurrent Events Data Analysis of Clustered Data Model Assessment Using Cumulative Sums of Martingale Residuals Bayesian Analysis of the Cox Model Bayesian Analysis of Piecewise Exponential Model
- References
| Partial Likelihood Function for the Cox Model |
Let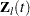 
denote the vector explanatory variables for the 
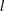th individual at time 
. Let 
denote the 
distinct, ordered event times. Let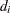 
denote the multiplicity of failures at 
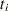; that is, 
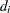is the size of the set 
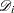of individuals that fail a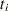t . Let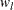 
be the weight associated with the 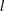th individual. Using this notation, the likelihood functions used in PROC PHREG to estimate 
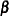are described in the following sections.
Continuous Time Scale
Let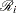 
denote the risk set just before the ith ordered event time 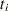. Let 
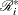denote the set of individuals whose event or censored times exceed 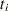or whose censored times are equal to .
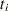Discrete Time Scale
Let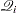 
denote the set of all subsets of 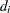individuals from the risk set 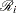. For each 
, 
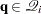is a 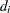-tuple 
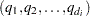of individuals who might have failed at .
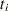Discrete Logistic Likelihood
 |
The computation of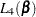 
and its derivatives is based on an adaptation of the recurrence algorithm of Gail, Lubin, and Rubinstein (1981) to the logarithmic scale. When there are no ties on the event times (that is, 
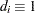), all four likelihood functions 
, 
, 
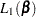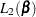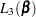, and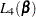 
reduce to the same expression. In a stratified analysis, the partial likelihood is the product of the partial likelihood functions for the individual strata.