The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG Statement ASSESS Statement BASELINE Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement ESTIMATE Statement FREQ Statement HAZARDRATIO Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements RANDOM Statement STRATA Statement SLICE Statement STORE Statement TEST Statement WEIGHT Statement
PROC PHREG Statement ASSESS Statement BASELINE Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement ESTIMATE Statement FREQ Statement HAZARDRATIO Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements RANDOM Statement STRATA Statement SLICE Statement STORE Statement TEST Statement WEIGHT Statement -
Details
 Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Counting Process Style of Input Left-Truncation of Failure Times The Multiplicative Hazards Model The Frailty Model Hazard Ratios Specifics for Classical Analysis Specifics for Bayesian Analysis Computational Resources Input and Output Data Sets Displayed Output ODS Table Names ODS Graphics
Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Counting Process Style of Input Left-Truncation of Failure Times The Multiplicative Hazards Model The Frailty Model Hazard Ratios Specifics for Classical Analysis Specifics for Bayesian Analysis Computational Resources Input and Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples
 Stepwise Regression Best Subset Selection Modeling with Categorical Predictors Firth’s Correction for Monotone Likelihood Conditional Logistic Regression for m:n Matching Model Using Time-Dependent Explanatory Variables Time-Dependent Repeated Measurements of a Covariate Survivor Function Estimates for Specific Covariate Values Analysis of Residuals Analysis of Recurrent Events Data Analysis of Clustered Data Model Assessment Using Cumulative Sums of Martingale Residuals Bayesian Analysis of the Cox Model Bayesian Analysis of Piecewise Exponential Model
Stepwise Regression Best Subset Selection Modeling with Categorical Predictors Firth’s Correction for Monotone Likelihood Conditional Logistic Regression for m:n Matching Model Using Time-Dependent Explanatory Variables Time-Dependent Repeated Measurements of a Covariate Survivor Function Estimates for Specific Covariate Values Analysis of Residuals Analysis of Recurrent Events Data Analysis of Clustered Data Model Assessment Using Cumulative Sums of Martingale Residuals Bayesian Analysis of the Cox Model Bayesian Analysis of Piecewise Exponential Model - References
| ESTIMATE Statement |
- ESTIMATE <'label'> estimate-specification <(divisor=n)>
<, <'label'> estimate-specification <(divisor=n)> > <, ...>
< / options> ;
The ESTIMATE statement provides a mechanism for obtaining custom hypothesis tests. Estimates are formed as linear estimable functions of the form 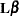 . You can perform hypothesis tests for the estimable functions, construct confidence limits, and obtain specific nonlinear transformations.
. You can perform hypothesis tests for the estimable functions, construct confidence limits, and obtain specific nonlinear transformations.
Table 66.4 summarizes important options in the ESTIMATE statement. If the BAYES statement is specified, the ADJUST=, STEPDOWN, TESTVALUE, LOWER, UPPER, and JOINT options are ignored. The PLOTS= option is not available for the maximum likelihood anaysis. It is available only for the Bayesian analysis.
Option |
Description |
|---|---|
Construction and Computation of Estimable Functions |
|
Specifies a list of values to divide the coefficients |
|
Suppresses the automatic fill-in of coefficients for higher-order effects |
|
Tunes the estimability checking difference |
|
Degrees of Freedom and p-values |
|
Determines the method for multiple comparison adjustment of estimates |
|
Determines the confidence level ( |
|
Performs one-sided, lower-tailed inference |
|
Adjusts multiplicity-corrected p-values further in a step-down fashion |
|
Specifies values under the null hypothesis for tests |
|
Performs one-sided, upper-tailed inference |
|
Statistical Output |
|
Constructs confidence limits |
|
Displays the correlation matrix of estimates |
|
Displays the covariance matrix of estimates |
|
Prints the |
|
Produces a joint |
|
Requests ODS statistical graphics if the analysis is sampling-based |
|
Specifies the seed for computations that depend on random numbers |
|
For details about the syntax of the ESTIMATE statement, see the section ESTIMATE Statement of Chapter 19, Shared Concepts and Topics.

 )
) 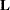 matrix
matrix 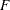 or chi-square test for the estimable functions
or chi-square test for the estimable functions