The NLIN Procedure

For unconstrained estimates (no active bounds), the covariance matrix of the parameter estimates is

for the gradient, Marquardt, and Gauss methods and

for the Newton method. Recall that 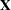is the matrix of the first partial derivatives of the nonlinear model with respect to the parameters. The matrices are evaluated at the final parameter estimates. The mean squared error, the estimate of the residual variance 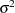, is computed as

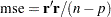where is the number of nonmissing (used) observations and is the number of estimable parameters. The standard error reported for the parameter estimates is the square root of the corresponding diagonal element of this matrix. If you specify a value for the residual variance with the SIGSQ= option, then that value replaces 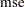in the preceding expressions.

Now suppose that restrictions or bounds are active. Equality restrictions can be written as a vector function, . Inequality restrictions are either active or inactive. When an inequality restriction is active, it is treated as an equality restriction.

Assume that the vector 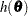contains the current active restrictions. The constraint matrix 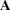is then

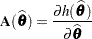The covariance matrix for the restricted parameter estimates is computed as

where is the Hessian (or approximation to the Hessian) and 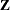collects the last 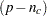columns of from an LQ factorization of the constraint matrix. Further, 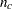is the number of active constraints, and denotes the number of parameters. See Gill, Murray, and Wright (1981) for more details about the LQ factorization. The covariance matrix for the Lagrange multipliers is computed as