The NLIN Procedure

The NLIN procedure performs univariate nonlinear regression by using the least squares method. Nonlinear regression analysis is indicated when the functional relationship between the response variable and the predictor variables is nonlinear. Nonlinearity in this context refers to a nonlinear relationship in the parameters. Many linear regression models exhibit a relationship in the regressor (predictor) variables that is not simply a straight line. This does not make the models nonlinear. A model is nonlinear in the parameters if the derivative of the model with respect to a parameter depends on this or other parameters.

Consider, for example the models

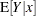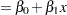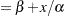In these expressions, denotes the expected value of the response variable 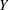at the fixed value of . (The conditioning on simply indicates that the predictor variables are assumed to be non-random in models fit by the NLIN procedure. Conditioning is often omitted for brevity in this chapter.)

Only the third model is a nonlinear model. The first model is a simple linear regression. It is linear in the parameters 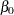and 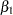since the model derivatives do not depend on unknowns:

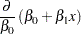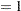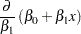The model is also linear in its relationship with (a straight line). The second model is also linear in the parameters, since

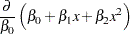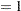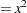It is a curvilinear model since it exhibits a curved relationship when plotted against . The third model, finally, is a nonlinear model since

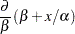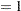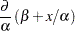The second of these derivatives depends on a parameter . A model is nonlinear if it is not linear in at least one parameter.