| The POWER Procedure |
| Summary of Analyses |
Table 68.27 gives a summary of the analyses supported in the POWER procedure. The name of the analysis statement reflects the type of data and design. The TEST=, CI=, and DIST= options specify the focus of the statistical hypothesis (in other words, the criterion on which the research question is based) and the test statistic to be used in data analysis.
Analysis |
Statement |
Options |
|---|---|---|
Logistic regression: likelihood ratio chi-square test |
||
Multiple linear regression: Type III |
||
Correlation: Fisher’s |
DIST=FISHERZ |
|
Correlation: |
||
Binomial proportion: exact test |
TEST=EXACT |
|
Binomial proportion: |
||
Binomial proportion: |
TEST=ADJZ |
|
Binomial proportion: exact equivalence test |
TEST=EQUIV_EXACT |
|
Binomial proportion: |
TEST=EQUIV_Z |
|
Binomial proportion: |
TEST=EQUIV_ADJZ |
|
Binomial proportion: confidence interval |
CI=AGRESTICOULL |
|
CI=JEFFREYS |
||
CI=EXACT |
||
CI=WALD |
||
CI=WALD_CORRECT |
||
CI=WILSON |
||
One-sample |
||
One-sample |
||
One-sample equivalence test for mean of normal data |
TEST=EQUIV |
|
One-sample equivalence test for mean of lognormal data |
||
Confidence interval for a mean |
CI=T |
|
One-way ANOVA: one-degree-of-freedom contrast |
TEST=CONTRAST |
|
One-way ANOVA: overall |
TEST=OVERALL |
|
McNemar exact conditional test |
||
McNemar normal approximation test |
DIST=NORMAL |
|
Paired |
TEST=DIFF |
|
Paired |
TEST=RATIO |
|
Paired additive equivalence of mean difference with normal data |
TEST=EQUIV_DIFF |
|
Paired multiplicative equivalence of mean ratio with lognormal data |
TEST=EQUIV_RATIO |
|
Confidence interval for mean of paired differences |
CI=DIFF |
|
Pearson chi-square test for two independent proportions |
TEST=PCHI |
|
Fisher’s exact test for two independent proportions |
TEST=FISHER |
|
Likelihood ratio chi-square test for two independent proportions |
TEST=LRCHI |
|
Two-sample |
TEST=DIFF |
|
Two-sample Satterthwaite |
TEST=DIFF_SATT |
|
Two-sample pooled |
TEST=RATIO |
|
Two-sample additive equivalence of mean difference with normal data |
TEST=EQUIV_DIFF |
|
Two-sample multiplicative equivalence of mean ratio with lognormal data |
TEST=EQUIV_RATIO |
|
Two-sample confidence interval for mean difference |
CI=DIFF |
|
Log-rank test for comparing two survival curves |
TEST=LOGRANK |
|
Gehan rank test for comparing two survival curves |
TEST=GEHAN |
|
Tarone-Ware rank test for comparing two survival curves |
TEST=TARONEWARE |
|
Wilcoxon-Mann-Whitney (rank-sum) test |
Copyright © SAS Institute, Inc. All Rights Reserved.
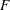 test
test  test
test  test
test