PROC POWER: TWOSAMPLEMEANS Statement :: SAS/STAT(R) 9.22 User's Guide

The POWER Procedure

TWOSAMPLEMEANS Statement

TWOSAMPLEMEANS <options> ;

The TWOSAMPLEMEANS statement performs power and sample size analyses for pooled and unpooled $\text{[math]}$ tests, equivalence tests, and confidence interval precision involving two independent samples.

Summary of Options

Table 68.21 summarizes categories of options available in the TWOSAMPLEMEANS statement.

Table 68.21 Summary of Options in the TWOSAMPLEMEANS Statement
Task	Options
Define analysis	CI=
	DIST=
	TEST=
Specify analysis information	ALPHA=
	LOWER=
	NULLDIFF=
	NULLRATIO=
	SIDES=
	UPPER=
Specify effects	HALFWIDTH=
	GROUPMEANS=
	MEANDIFF=
	MEANRATIO=
Specify variability	CV=
	GROUPSTDDEVS==
	STDDEV=
Specify sample size and allocation	GROUPNS=
	GROUPWEIGHTS=
	NPERGROUP=
	NTOTAL=
Specify power and related	POWER=
probabilities	PROBTYPE=
	PROBWIDTH=
Control sample size rounding	NFRACTIONAL
Control ordering in output	OUTPUTORDER=

Table 68.22 summarizes the valid result parameters for different analyses in the TWOSAMPLEMEANS statement.

Table 68.22 Summary of Result Parameters in the TWOSAMPLEMEANS Statement
Analyses	Solve For	Syntax
TEST=DIFF	Power	POWER=.
	Sample size	NTOTAL=.
		NPERGROUP=.
	Group sample size	GROUPNS= n1 \| .
		GROUPNS=. \| n2
		GROUPNS= (n1 .)
		GROUPNS= (. n2)
	Group weight	GROUPWEIGHTS= w1 \| .
		GROUPWEIGHTS=. \| w2
		GROUPWEIGHTS= (w1 .)
		GROUPWEIGHTS= (. w2)
	Alpha	ALPHA=.
	Group mean	GROUPMEANS= mean1 \| .
		GROUPMEANS=. \| mean2
		GROUPMEANS= (mean1 .)
		GROUPMEANS= (. mean2)
	Mean difference	MEANDIFF=.
	Standard deviation	STDDEV=.
TEST=DIFF_SATT	Power	POWER=.
	Sample size	NTOTAL=.
		NPERGROUP=.
TEST=RATIO	Power	POWER=.
	Sample size	NTOTAL=.
		NPERGROUP=.
TEST=EQUIV_DIFF	Power	POWER=.
	Sample size	NTOTAL=.
		NPERGROUP=.
TEST=EQUIV_RATIO	Power	POWER=.
	Sample size	NTOTAL=.
		NPERGROUP=.
CI=DIFF	Prob(width)	PROBWIDTH=.
	Sample size	NTOTAL=.
		NPERGROUP=.

Dictionary of Options

ALPHA=number-list

specifies the level of significance of the statistical test or requests a solution for alpha with a missing value (ALPHA=.). The default is 0.05, corresponding to the usual 0.05 $\text{[math]}$ 100% = 5% level of significance. If the CI= and SIDES=1 options are used, then the value must be less than 0.5. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

CI

CI=DIFF

specifies an analysis of precision of the confidence interval for the mean difference, assuming equal variances. Instead of power, the relevant probability for this analysis is the probability that the interval half-width is at most the value specified by the HALFWIDTH= option. If neither the TEST= option nor the CI= option is used, the default is TEST=DIFF.

CV=number-list

specifies the coefficient of variation assumed to be common to both groups. The coefficient of variation is defined as the ratio of the standard deviation to the mean. You can use this option only with DIST=LOGNORMAL. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

DIST=LOGNORMAL

DIST=NORMAL

specifies the underlying distribution assumed for the test statistic. NORMAL corresponds the normal distribution, and LOGNORMAL corresponds to the lognormal distribution. The default value (also the only acceptable value in each case) is NORMAL for TEST=DIFF, TEST=DIFF_SATT, TEST=EQUIV_DIFF, and CI=DIFF; and LOGNORMAL for TEST=RATIO and TEST=EQUIV_RATIO.

GROUPMEANS=grouped-number-list

GMEANS=grouped-number-list

specifies the two group means or requests a solution for one group mean given the other. Means are in the original scale. They are arithmetic if DIST=NORMAL and geometric if DIST=LOGNORMAL. This option cannot be used with the CI=DIFF analysis. When TEST=EQUIV_DIFF, the means are interpreted as the reference mean (first) and the treatment mean (second). See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-number-list.

GROUPNS=grouped-number-list

GNS=grouped-number-list

specifies the two group sample sizes or requests a solution for one group sample size given the other. See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-number-list.

GROUPSTDDEVS=grouped-number-list

GSTDDEVS=grouped-number-list

GROUPSTDS=grouped-number-list

GSTDS=grouped-number-list

specifies the standard deviation of each group. Unlike the STDDEV= option, the GROUPSTDDEVS== option supports different values for each group. It is valid only for the Satterthwaite $\text{[math]}$ test (TEST=DIFF_SATT DIST=NORMAL). See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-number-list.

GROUPWEIGHTS=grouped-number-list

GWEIGHTS=grouped-number-list

specifies the sample size allocation weights for the two groups, or requests a solution for one group weight given the other. This option controls how the total sample size is divided between the two groups. Each pair of values for the two groups represents relative allocation weights. Additionally, if the NFRACTIONAL option is not used, the total sample size is restricted to be equal to a multiple of the sum of the two group weights (so that the resulting design has an integer sample size for each group while adhering exactly to the group allocation weights). Values must be integers unless the NFRACTIONAL option is used. The default value is (1 1), a balanced design with a weight of 1 for each group. See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-number-list.

HALFWIDTH=number-list

specifies the desired confidence interval half-width. The half-width is defined as the distance between the point estimate and a finite endpoint. This option can be used only with the CI=DIFF analysis. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

LOWER=number-list

specifies the lower equivalence bound for the mean difference or mean ratio, in the original scale (whether DIST=NORMAL or DIST=LOGNORMAL). Values must be greater than 0 when DIST=LOGNORMAL. This option can be used only with the TEST=EQUIV_DIFF and TEST=EQUIV_RATIO analyses. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

MEANDIFF=number-list

specifies the mean difference, defined as 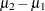$\text{[math]}$ , or requests a solution for the mean difference with a missing value (MEANDIFF=.). This option can be used only with the TEST=DIFF, TEST=DIFF_SATT, and TEST=EQUIV_DIFF analyses. When TEST=EQUIV_DIFF, the mean difference is interpreted as the treatment mean minus the reference mean. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

MEANRATIO=number-list

specifies the geometric mean ratio, defined as 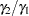$\text{[math]}$ . This option can be used only with the TEST=RATIO and TEST=EQUIV_RATIO analyses. When TEST=EQUIV_RATIO, the mean ratio is interpreted as the treatment mean divided by the reference mean. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

NFRACTIONAL

NFRAC

enables fractional input and output for sample sizes. See the section Sample Size Adjustment Options for information about the ramifications of the presence (and absence) of the NFRACTIONAL option.

NPERGROUP=number-list

NPERG=number-list

specifies the common sample size per group or requests a solution for the common sample size per group with a missing value (NPERGROUP=.). Use of this option implicitly specifies a balanced design. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

NTOTAL=number-list

specifies the sample size or requests a solution for the sample size with a missing value (NTOTAL=.). See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

NULLDIFF=number-list

NULLD=number-list

specifies the null mean difference. The default value is 0. This option can be used only with the TEST=DIFF and TEST=DIFF_SATT analyses. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

NULLRATIO=number-list

NULLR=number-list

specifies the null mean ratio. The default value is 1. This option can be used only with the TEST=RATIO analysis. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

OUTPUTORDER=INTERNAL

OUTPUTORDER=REVERSE

OUTPUTORDER=SYNTAX

controls how the input and default analysis parameters are ordered in the output. OUTPUTORDER=INTERNAL (the default) arranges the parameters in the output according to the following order of their corresponding options:

The OUTPUTORDER=SYNTAX option arranges the parameters in the output in the same order in which their corresponding options are specified in the TWOSAMPLEMEANS statement. The OUTPUTORDER=REVERSE option arranges the parameters in the output in the reverse of the order in which their corresponding options are specified in the TWOSAMPLEMEANS statement.

POWER=number-list

specifies the desired power of the test or requests a solution for the power with a missing value (POWER=.). The power is expressed as a probability, a number between 0 and 1, rather than as a percentage. This option cannot be used with the CI=DIFF analysis. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

PROBTYPE=keyword-list

specifies the type of probability for the PROBWIDTH= option. A value of CONDITIONAL (the default) indicates the conditional probability that the confidence interval half-width is at most the value specified by the HALFWIDTH= option, given that the true mean difference is captured by the confidence interval. A value of UNCONDITIONAL indicates the unconditional probability that the confidence interval half-width is at most the value specified by the HALFWIDTH= option. you can use the alias GIVENVALIDITY for CONDITIONAL. The PROBTYPE= option can be used only with the CI=DIFF analysis. See the section Specifying Value Lists in Analysis Statements for information about specifying the keyword-list.

CONDITIONAL: width probability conditional on interval containing the mean
UNCONDITIONAL: unconditional width probability

PROBWIDTH=number-list

specifies the desired probability of obtaining a confidence interval half-width less than or equal to the value specified by the HALFWIDTH= option. A missing value (PROBWIDTH=.) requests a solution for this probability. The type of probability is controlled with the PROBTYPE= option. Values are expressed as probabilities (for example, 0.9) rather than percentages. This option can be used only with the CI=DIFF analysis. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

SIDES=keyword-list

specifies the number of sides (or tails) and the direction of the statistical test or confidence interval. See the section Specifying Value Lists in Analysis Statements for information about specifying the keyword-list. Valid keywords and their interpretation for the TEST= analyses are as follows:

1: one-sided with alternative hypothesis in same direction as effect
2: two-sided
U: upper one-sided with alternative greater than null value
L: lower one-sided with alternative less than null value

For confidence intervals, SIDES=U refers to an interval between the lower confidence limit and infinity, and SIDES=L refers to an interval between minus infinity and the upper confidence limit. For both of these cases and SIDES=1, the confidence interval computations are equivalent. The SIDES= option cannot be used with the TEST=EQUIV_DIFF and TEST=EQUIV_RATIO analyses. The default value is 2.

STDDEV=number-list

STD=number-list

specifies the standard deviation assumed to be common to both groups, or requests a solution for the common standard deviation with a missing value (STDDEV=.). This option can be used only with DIST=NORMAL. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

TEST

TEST=DIFF

TEST=DIFF_SATT

TEST=EQUIV_DIFF

TEST=EQUIV_RATIO

TEST=RATIO

specifies the statistical analysis. TEST or TEST=DIFF (the default) specifies a pooled $\text{[math]}$ test on the mean difference, assuming equal variances. TEST=DIFF_SATT specifies a Satterthwaite unpooled $\text{[math]}$ test on the mean difference, assuming unequal variances. TEST=EQUIV_DIFF specifies an additive equivalence test of the mean difference by using a two one-sided tests (TOST) analysis (Schuirman 1987). TEST=EQUIV_RATIO specifies a multiplicative equivalence test of the mean ratio by using a TOST analysis. TEST=RATIO specifies a pooled $\text{[math]}$ test on the mean ratio, assuming equal coefficients of variation. If neither the TEST= option nor the CI= option is used, the default is TEST=DIFF.

UPPER=number-list

specifies the upper equivalence bound for the mean difference or mean ratio, in the original scale (whether DIST=NORMAL or DIST=LOGNORMAL). This option can be used only with the TEST=EQUIV_DIFF and TEST=EQUIV_RATIO analyses. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.

Restrictions on Option Combinations

To define the analysis, choose one of the following parameterizations:

a statistical test (by using the TEST= option)
confidence interval precision (by using the CI= option)

To specify the means, choose one of the following parameterizations:

individual group means (by using the GROUPMEANS= option)
mean difference (by using the MEANDIFF= option)
mean ratio (by using the MEANRATIO= option)

To specify standard deviations in the Satterthwaite $\text{[math]}$ test (TEST=DIFF_SATT), choose one of the following parameterizations:

common standard deviation (by using the STDDEV= option)
individual group standard deviations (by using the GROUPSTDDEVS== option)

To specify the sample sizes and allocation, choose one of the following parameterizations:

sample size per group in a balanced design (by using the NPERGROUP= option)
total sample size and allocation weights (by using the NTOTAL= and GROUPWEIGHTS= options)
individual group sample sizes (by using the GROUPNS= option)

Option Groups for Common Analyses

This section summarizes the syntax for the common analyses supported in the TWOSAMPLEMEANS statement.

Two-Sample t Test Assuming Equal Variances

You can use the NPERGROUP= option in a balanced design and express effects in terms of the mean difference, as in the following statements. Default values for the DIST=, SIDES=, NULLDIFF=, and ALPHA= options specify a two-sided test for no difference with a normal distribution and a significance level of 0.05.

proc power;
   twosamplemeans test=diff
      meandiff = 7
      stddev = 12
      npergroup = 50
      power = .;
run;

You can also specify an unbalanced design by using the NTOTAL= and GROUPWEIGHTS= options and express effects in terms of individual group means:

proc power;
   twosamplemeans test=diff
      groupmeans = 8 | 15
      stddev = 4
      groupweights = (2 3)
      ntotal = .
      power = 0.9;
run;

Another way to specify the sample sizes is with the GROUPNS= option:

proc power;
   twosamplemeans test=diff
      groupmeans = 8 | 15
      stddev = 4
      groupns = (25 40)
      power = .;
run;

Two-Sample Satterthwaite t Test Assuming Unequal Variances

The following statements demonstrate a power computation for the two-sample Satterthwaite t test allowing unequal variances. Default values for the DIST=, SIDES=, NULLDIFF=, and ALPHA= options specify a two-sided test for no difference with a normal distribution and a significance level of 0.05.

proc power;
   twosamplemeans test=diff_satt
      meandiff = 3
      groupstddevs = 5 | 8
      groupweights = (1 2)
      ntotal = 60
      power = .;
run;

Two-Sample Pooled t Test of Mean Ratio with Lognormal Data

The following statements demonstrate a power computation for the pooled t test of a lognormal mean ratio. Default values for the DIST=, SIDES=, NULLRATIO=, and ALPHA= options specify a two-sided test of mean ratio = 1 assuming a lognormal distribution and a significance level of 0.05.

proc power;
   twosamplemeans test=ratio
      meanratio = 7
      cv = 0.8
      groupns = 50 | 70
      power = .;
run;

Additive Equivalence Test for Mean Difference with Normal Data

The following statements demonstrate a sample size computation for the TOST equivalence test for a normal mean difference. A default value of GROUPWEIGHTS=(1 1) specifies a balanced design. Default values for the DIST= and ALPHA= options specify a significance level of 0.05 and an assumption of normally distributed data.

proc power;
   twosamplemeans test=equiv_diff
      lower = 2
      upper = 5
      meandiff = 4
      stddev = 8
      ntotal = .
      power = 0.9;
run;

Multiplicative Equivalence Test for Mean Ratio with Lognormal Data

The following statements demonstrate a power computation for the TOST equivalence test for a lognormal mean ratio. Default values for the DIST= and ALPHA= options specify a significance level of 0.05 and an assumption of lognormally distributed data.

proc power;
   twosamplemeans test=equiv_ratio
      lower = 3
      upper = 7
      meanratio = 5
      cv = 0.75
      npergroup = 50
      power = .;
run;

Confidence Interval for Mean Difference

By default CI=DIFF analyzes the conditional probability of obtaining the desired precision, given that the interval contains the true mean difference, as in the following statements. The defaults of SIDES=2 and ALPHA=0.05 specify a two-sided interval with a confidence level of 0.95.

proc power;
   twosamplemeans ci = diff
      halfwidth = 4
      stddev = 8
      groupns = (30 35)
      probwidth = .;
run;

Top of Page