| The POWER Procedure |
| LOGISTIC Statement |
The LOGISTIC statement performs power and sample size analyses for the likelihood ratio chi-square test of a single predictor in binary logistic regression, possibly in the presence of one or more covariates. All predictor variables are assumed to be independent of each other. So, this analysis is not applicable to studies with correlated predictors—for example, most observational studies (as opposed to randomized studies).
Summary of Options
Table 68.2 summarizes categories of options available in the LOGISTIC statement.
Task |
Options |
|---|---|
Define analysis |
|
Specify analysis information |
|
Specify effects |
|
Specify sample size |
|
Specify power |
|
Control sample size rounding |
|
Specify computational method |
|
Control ordering in output |
Table 68.3 summarizes the valid result parameters in the LOGISTIC statement.
Analyses |
Solve For |
Syntax |
|---|---|---|
TEST=LRCHI |
Power |
|
Sample size |
Dictionary of Options
- ALPHA=number-list
specifies the level of significance of the statistical test. The default is 0.05, corresponding to the usual 0.05
 100% = 5% level of significance. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.
100% = 5% level of significance. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list. - COVARIATES=grouped-name-list
specifies the distributions of any predictor variables in the model but not being tested, using labels specified with the VARDIST= option. The distributions are assumed to be independent of each other and of the tested predictor. If this option is omitted, then the tested predictor specified by the TESTEDPREDICTOR= option is assumed to be the only predictor in the model. See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-name-list.
- COVODDSRATIOS=grouped-number-list
specifies the odds ratios for the covariates in the full model (including variables in the TESTPREDICTOR= and COVARIATES= options). The ordering of the values corresponds to the ordering in the COVARIATES= option. If the response variable is coded as
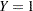 for success and
for success and 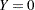 for failure, then the odds ratio for each covariate
for failure, then the odds ratio for each covariate  is the odds of
is the odds of 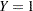 when
when 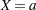 divided by the odds of
divided by the odds of 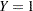 when
when 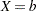 , where
, where  and
and 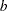 are determined from the DEFAULTUNIT= and UNITS= options. Values must be greater than zero. See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-number-list.
are determined from the DEFAULTUNIT= and UNITS= options. Values must be greater than zero. See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-number-list. - COVREGCOEFFS=grouped-number-list
specifies the regression coefficients for the covariates in the full model including the test predictor (as specified by the TESTPREDICTOR= option). The ordering of the values corresponds to the ordering in the COVARIATES= option. See the section Specifying Value Lists in Analysis Statements for information about specifying the grouped-number-list.
- DEFAULTNBINS=number
specifies the default number of categories (or "bins") into which the distribution for each predictor variable is divided in internal calculations. Higher values increase computational time and memory requirements but generally lead to more accurate results. Each test predictor or covariate that is absent from the NBINS= option derives its bin number from the DEFAULTNBINS= option. The default value is DEFAULTNBINS=10.
There are two variable distributions for which the number of bins can be overridden internally:
For an ordinal distribution, the number of ordinal values is always used as the number of bins.
For a binomial distribution, if the requested number of bins is larger than
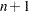 , where n is the sample size parameter of the binomial distribution, then exactly
, where n is the sample size parameter of the binomial distribution, then exactly 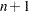 bins are used.
bins are used.
- DEFAULTUNIT=change-spec
specifies the default change in the predictor variables assumed for odds ratios specified with the COVODDSRATIOS= and TESTODDSRATIO= options. Each test predictor or covariate that is absent from the UNITS= option derives its change value from the DEFAULTUNIT= option. The value must be nonzero. The default value is DEFAULTUNIT=1. This option can be used only if at least one of the COVODDSRATIOS= and TESTODDSRATIO= options is used.
Valid specifications for change-spec are as follows:
- number
defines the odds ratio as the ratio of the response variable odds when
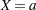 to the odds when
to the odds when  for any constant
for any constant  .
. - <+ | ->SD
defines the odds ratio as the ratio of the odds when
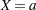 to the odds when
to the odds when 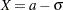 (or
(or 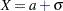 , if SD is preceded by a minus sign (–)) for any constant
, if SD is preceded by a minus sign (–)) for any constant  , where
, where  is the standard deviation of
is the standard deviation of  (as determined from the VARDIST= option).
(as determined from the VARDIST= option). - multiple*SD
defines the odds ratio as the ratio of the odds when
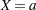 to the odds when
to the odds when  for any constant
for any constant  , where
, where  is the standard deviation of
is the standard deviation of  (as determined from the VARDIST= option).
(as determined from the VARDIST= option). - PERCENTILES(p1, p2)
defines the odds ratio as the ratio of the odds when
 is equal to its
is equal to its 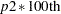 percentile to the odds when
percentile to the odds when  is equal to its
is equal to its  percentile (where the percentiles are determined from the distribution specified in the VARDIST= option). Values for p1 and p2 must be strictly between 0 and 1.
percentile (where the percentiles are determined from the distribution specified in the VARDIST= option). Values for p1 and p2 must be strictly between 0 and 1.
- INTERCEPT=number-list
specifies the intercept in the full model (including variables in the TESTPREDICTOR= and COVARIATES= options). See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.
- NBINS=("name" = number <..."name" = number>)
specifies the number of categories (or "bins") into which the distribution for each predictor variable (identified by its name from the VARDIST= option) is divided in internal calculations. Higher values increase computational time and memory requirements but generally lead to more accurate results. Each predictor variable that is absent from the NBINS= option derives its bin number from the DEFAULTNBINS= option.
There are two variable distributions for which the NBINS= value can be overridden internally:
For an ordinal distribution, the number of ordinal values is always used as the number of bins.
For a binomial distribution, if the requested number of bins is larger than
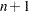 , where n is the sample size parameter of the binomial distribution, then exactly
, where n is the sample size parameter of the binomial distribution, then exactly 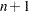 bins are used.
bins are used.
- NFRACTIONAL
- NFRAC
enables fractional input and output for sample sizes. See the section Sample Size Adjustment Options for information about the ramifications of the presence (and absence) of the NFRACTIONAL option.
- NTOTAL=number-list
specifies the sample size or requests a solution for the sample size with a missing value (NTOTAL=.). Values must be at least one. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.
- OUTPUTORDER=INTERNAL
- OUTPUTORDER=REVERSE
- OUTPUTORDER=SYNTAX
controls how the input and default analysis parameters are ordered in the output. OUTPUTORDER=INTERNAL (the default) arranges the parameters in the output according to the following order of their corresponding options:
The OUTPUTORDER=SYNTAX option arranges the parameters in the output in the same order in which their corresponding options are specified in the LOGISTIC statement. The OUTPUTORDER=REVERSE option arranges the parameters in the output in the reverse of the order in which their corresponding options are specified in the LOGISTIC statement.
- POWER=number-list
specifies the desired power of the test or requests a solution for the power with a missing value (POWER=.). The power is expressed as a probability, a number between 0 and 1, rather than as a percentage. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.
- RESPONSEPROB=number-list
specifies the response probability in the full model when all predictor variables (including variables in the TESTPREDICTOR= and COVARIATES= options) are equal to their means. The log odds of this probability are equal to the intercept in the full model where all predictor are centered at their means. If the response variable is coded as
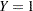 for success and
for success and 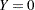 for failure, then this probability is equal to the mean of
for failure, then this probability is equal to the mean of 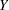 in the full model when all Xs are equal to their means. Values must be strictly between zero and one. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.
in the full model when all Xs are equal to their means. Values must be strictly between zero and one. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list. - TEST=LRCHI
specifies the likelihood ratio chi-square test of a single model parameter in binary logistic regression. This is the default test option.
- TESTODDSRATIO=number-list
specifies the odds ratio for the predictor variable being tested in the full model (including variables in the TESTPREDICTOR= and COVARIATES= options). If the response variable is coded as
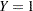 for success and
for success and 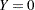 for failure, then the odds ratio for the
for failure, then the odds ratio for the  being tested is the odds of
being tested is the odds of 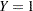 when
when 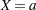 divided by the odds of
divided by the odds of 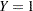 when
when 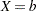 , where
, where  and
and 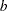 are determined from the DEFAULTUNIT= and UNITS= options. Values must be greater than zero. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.
are determined from the DEFAULTUNIT= and UNITS= options. Values must be greater than zero. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list. - TESTPREDICTOR=name-list
specifies the distribution of the predictor variable being tested, using labels specified with the VARDIST= option. This distribution is assumed to be independent of the distributions of the covariates as defined in the COVARIATES= option. See the section Specifying Value Lists in Analysis Statements for information about specifying the name-list.
- TESTREGCOEFF=number-list
specifies the regression coefficient for the predictor variable being tested in the full model including the covariates specified by the COVARIATES= option. See the section Specifying Value Lists in Analysis Statements for information about specifying the number-list.
- UNITS=("name" = change-spec <..."name" = change-spec>)
specifies the changes in the predictor variables assumed for odds ratios specified with the COVODDSRATIOS= and TESTODDSRATIO= options. Each predictor variable whose name (from the VARDIST= option) is absent from the UNITS option derives its change value from the DEFAULTUNIT= option. This option can be used only if at least one of the COVODDSRATIOS= and TESTODDSRATIO= options is used.
Valid specifications for change-spec are as follows:
- number
defines the odds ratio as the ratio of the response variable odds when
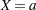 to the odds when
to the odds when  for any constant
for any constant  .
. - <+ | ->SD
defines the odds ratio as the ratio of the odds when
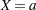 to the odds when
to the odds when 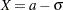 (or
(or 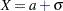 , if SD is preceded by a minus sign (–)) for any constant
, if SD is preceded by a minus sign (–)) for any constant  , where
, where  is the standard deviation of
is the standard deviation of  (as determined from the VARDIST= option).
(as determined from the VARDIST= option). - multiple*SD
defines the odds ratio as the ratio of the odds when
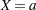 to the odds when
to the odds when  for any constant
for any constant  , where
, where  is the standard deviation of
is the standard deviation of  (as determined from the VARDIST= option).
(as determined from the VARDIST= option). - PERCENTILES(p1, p2)
defines the odds ratio as the ratio of the odds when
 is equal to its
is equal to its 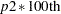 percentile to the odds when
percentile to the odds when  is equal to its
is equal to its  percentile (where the percentiles are determined from the distribution specified in the VARDIST= option). Values for p1 and p2 must be strictly between 0 and 1.
percentile (where the percentiles are determined from the distribution specified in the VARDIST= option). Values for p1 and p2 must be strictly between 0 and 1.
Each unit value must be nonzero.
- VARDIST("label")=distribution (parameters)
defines a distribution for a predictor variable.
For the VARDIST= option,
- label
identifies the variable distribution in the output and with the COVARIATES= and TESTPREDICTOR= options.
- distribution
specifies the distributional form of the variable.
- parameters
specifies one or more parameters associated with the distribution.
Choices for distributional forms and their parameters are as follows:
- ORDINAL ((values) : (probabilities))
is an ordered categorical distribution. The values are any numbers separated by spaces. The probabilities are numbers between 0 and 1 (inclusive) separated by spaces. Their sum must be exactly 1. The number of probabilities must match the number of values.
- BETA (a, b <, l, r >)
is a beta distribution with shape parameters
 and
and 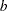 and optional location parameters
and optional location parameters  and
and  . The values of
. The values of  and
and 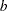 must be greater than 0, and
must be greater than 0, and  must be less than
must be less than  . The default values for
. The default values for  and
and  are 0 and 1, respectively.
are 0 and 1, respectively. - BINOMIAL (p, n)
is a binomial distribution with probability of success
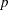 and number of independent Bernoulli trials
and number of independent Bernoulli trials  . The value of
. The value of 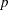 must be greater than 0 and less than 1, and
must be greater than 0 and less than 1, and  must be an integer greater than 0.
must be an integer greater than 0. - EXPONENTIAL (
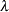 )
) is an exponential distribution with scale
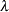 , which must be greater than 0.
, which must be greater than 0. - GAMMA (a,
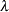 )
) is a gamma distribution with shape
 and scale
and scale 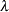 . The values of
. The values of  and
and 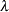 must be greater than 0.
must be greater than 0. - LAPLACE (
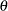 ,
, 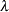 )
) is a Laplace distribution with location
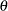 and scale
and scale 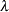 . The value of
. The value of 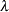 must be greater than 0.
must be greater than 0. - LOGISTIC (
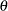 ,
, 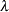 )
) is a logistic distribution with location
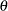 and scale
and scale 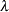 . The value of
. The value of 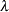 must be greater than 0.
must be greater than 0. - LOGNORMAL (
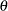 ,
, 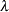 )
) is a lognormal distribution with location
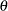 and scale
and scale 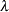 . The value of
. The value of 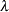 must be greater than 0.
must be greater than 0. - NORMAL (
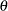 ,
, 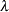 )
) is a normal distribution with mean
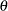 and standard deviation
and standard deviation 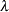 . The value of
. The value of 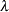 must be greater than 0.
must be greater than 0. - POISSON (m)
is a Poisson distribution with mean
 . The value of
. The value of  must be greater than 0.
must be greater than 0. - UNIFORM (l, r)
is a uniform distribution on the interval
 , where
, where  .
.
Restrictions on Option Combinations
To specify the intercept in the full model, choose one of the following two parameterizations:
intercept (using the INTERCEPT= options)
Prob(
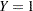 ) when all predictors are equal to their means (using the RESPONSEPROB= option)
) when all predictors are equal to their means (using the RESPONSEPROB= option)
To specify the effect associated with the predictor variable being tested, choose one of the following two parameterizations:
odds ratio (using the TESTODDSRATIO= options)
regression coefficient (using the TESTREGCOEFFS= option)
To describe the effects of the covariates in the full model, choose one of the following two parameterizations:
odds ratios (using the COVODDSRATIOS= options)
regression coefficients (using the COVREGCOEFFS= options)
Option Groups for Common Analyses
This section summarizes the syntax for the common analyses supported in the LOGISTIC statement.
Likelihood Ratio Chi-Square Test for One Predictor
You can express effects in terms of response probability and odds ratios, as in the following statements:
proc power;
logistic
vardist("x1a") = normal(0, 2)
vardist("x1b") = normal(0, 3)
vardist("x2") = poisson(7)
vardist("x3a") = ordinal((-5 0 5) : (.3 .4 .3))
vardist("x3b") = ordinal((-5 0 5) : (.4 .3 .3))
testpredictor = "x1a" "x1b"
covariates = "x2" | "x3a" "x3b"
responseprob = 0.15
testoddsratio = 1.75
covoddsratios = (2.1 1.4)
ntotal = 100
power = .;
run;
The VARDIST= options define the distributions of the predictor variables. The TESTPREDICTOR= option specifies two scenarios for the test predictor distribution, Normal(10,2) and Normal(10,3). The COVARIATES= option specifies two covariates, the first with a Poisson(7) distribution. The second covariate has an ordinal distribution on the values –5, 0, and 5 with two scenarios for the associated probabilities: (.3, .4, .3) and (.4, .3, .3). The response probability in the full model with all variables equal to zero is specified by the RESPONSEPROB= option as 0.15. The odds ratio for a unit decrease in the tested predictor is specified by the TESTODDSRATIO= option to be 1.75. Corresponding odds ratios for the two covariates in the full model are specified by the COVODDSRATIOS= option to be 2.1 and 1.4. The POWER=. option requests a solution for the power at a sample size of 100 as specified by the NTOTAL= option.
Default values of the TEST= and ALPHA= options specify a likelihood ratio test of the first predictor with a significance level of 0.05. The default of DEFAULTUNIT=1 specifies that all odds ratios are defined in terms of unit changes in predictors. The default of DEFAULTNBINS=10 specifies that each of the three predictor variables is discretized into a distribution with 10 categories in internal calculations.
You can also express effects in terms of regression coefficients, as in the following statements:
proc power;
logistic
vardist("x1a") = normal(0, 2)
vardist("x1b") = normal(0, 3)
vardist("x2") = poisson(7)
vardist("x3a") = ordinal((-5 0 5) : (.3 .4 .3))
vardist("x3b") = ordinal((-5 0 5) : (.4 .3 .3))
testpredictor = "x1a" "x1b"
covariates = "x2" | "x3a" "x3b"
intercept = -6.928162
testregcoeff = 0.5596158
covregcoeffs = (0.7419373 0.3364722)
ntotal = 100
power = .;
run;
The regression coefficients for the tested predictor (TESTREGCOEFF=0.5596158) and covariates (COVREGCOEFFS=(0.7419373 0.3364722)) are determined by taking the logarithm of the corresponding odds ratios. The intercept in the full model is specified as –6.928162 by the INTERCEPT= option. This number is calculated according to the forumula at the end of Analyses in the LOGISTIC Statement, which expresses the intercept in terms of the response probability, regression coefficients, and predictor means:
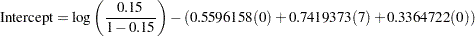 |
Copyright © SAS Institute, Inc. All Rights Reserved.