| The POWER Procedure |
Analyses in the LOGISTIC Statement
Likelihood Ratio Chi-Square Test for One Predictor (TEST=LRCHI)
The power computing formula is based on Shieh and O’Brien (1998), Shieh (2000), and Self, Mauritsen, and Ohara (1992).
Define the following notation for a logistic regression analysis:
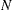 |
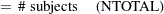 |
|||
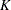 |
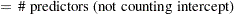 |
|||
 |
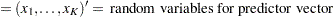 |
|||
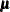 |
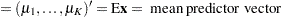 |
|||
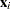 |
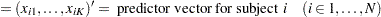 |
|||
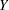 |
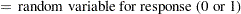 |
|||
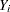 |
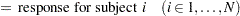 |
|||
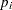 |
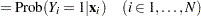 |
|||
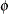 |
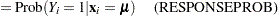 |
|||
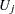 |
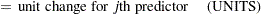 |
|||
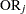 |
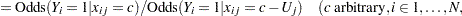 |
|||
 |
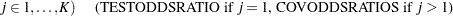 |
|||
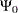 |
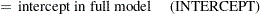 |
|||
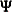 |
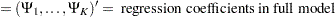 |
|||
 |
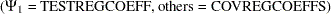 |
|||
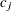 |
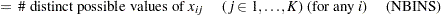 |
|||
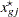 |
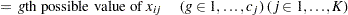 |
|||
 |
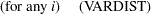 |
|||
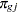 |
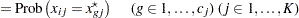 |
|||
 |
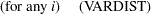 |
|||
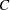 |
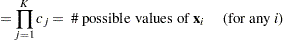 |
|||
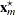 |
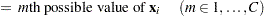 |
|||
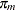 |
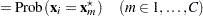 |
The logistic regression model is
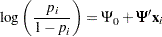 |
The hypothesis test of the first predictor variable is
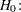 |
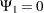 |
|||
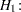 |
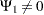 |
Assuming independence among all predictor variables, 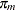 is defined as follows:
is defined as follows:
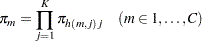 |
where 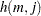 is calculated according to the following algorithm:
is calculated according to the following algorithm:
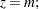 |
|||||
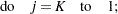 |
|||||
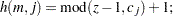 |
|||||
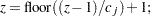 |
|||||
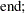 |
|||||
This algorithm causes the elements of the transposed vector 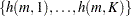 to vary fastest to slowest from right to left as
to vary fastest to slowest from right to left as  increases, as shown in the following table of
increases, as shown in the following table of 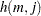 values:
values:
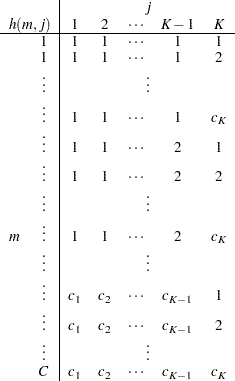 |
The 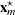 values are determined in a completely analogous manner.
values are determined in a completely analogous manner.
The discretization is handled as follows (unless the distribution is ordinal, or binomial with sample size parameter at least as large as requested number of bins): for 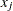 , generate
, generate 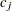 quantiles at evenly spaced probability values such that each such quantile is at the midpoint of a bin with probability
quantiles at evenly spaced probability values such that each such quantile is at the midpoint of a bin with probability 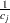 . In other words,
. In other words,
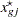 |
 |
|||
 |
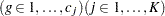 |
|||
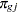 |
 |
The primary noncentrality for the power computation is
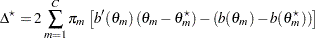 |
where
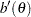 |
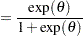 |
|||
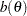 |
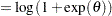 |
|||
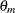 |
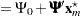 |
|||
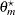 |
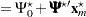 |
where
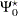 |
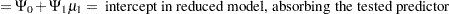 |
|||
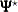 |
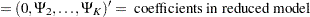 |
The power is
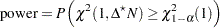 |
Alternative input parameterizations are handled by the following transformations:
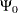 |
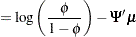 |
|||
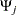 |
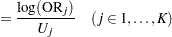 |
Copyright © SAS Institute, Inc. All Rights Reserved.