The HPQUANTSELECT Procedure
Example 14.1 Simulation Study
This example is based on Simulation Study in SAS/STAT 14.1 User's Guide. This simulation study shows how you can use the forward selection method to select quantile regression models for single quantile levels. The following statements simulate a data set from a naive instrumental model (Chernozhukov and Hansen 2008):
%let seed=321;
%let p=20;
%let n=3000;
data analysisData;
array x{&p} x1-x&p;
do i=1 to &n;
U = ranuni(&seed);
x1 = ranuni(&seed);
x2 = ranexp(&seed);
x3 = abs(rannor(&seed));
y = x1*(U-0.1) + x2*(U*U-0.25) + x3*(exp(U)-exp(0.9));
do j=4 to &p;
x{j} = ranuni(&seed);
end;
output;
end;
run;
Variable U in the data set indicates the true quantile level of the response y conditional on 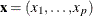 .
.
Let 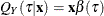 denote the underlying quantile regression model, where
denote the underlying quantile regression model, where 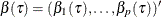 . Then, the true parameter functions are
. Then, the true parameter functions are
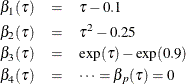
It is easy to see that, at 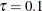 , only
, only 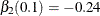 and
and 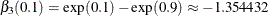 are nonzero parameters. Therefore, an effective effect-selection method should select
are nonzero parameters. Therefore, an effective effect-selection method should select x2 and x3 and drop all the other effects in this data set at 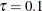 . By the same rationale,
. By the same rationale, x1 and x3 should be selected at 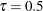 with
with 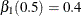 and
and 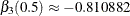 , and
, and x1 and x2 should be selected at 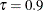 with
with 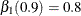 and
and 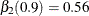 .
.
The following statements use PROC HPQUANTSELECT with the forward selection method. The STB option and the CLB option in the MODEL statement request the standardized parameter estimates and the confidence limits of parameter estimates, respectively.
proc hpquantselect data=analysisData; model y= x1-x&p / quantile=0.1 0.5 0.9 stb clb; selection method=forward; output out=out p=pred; run;
Output 14.1.1 shows that, by default, the CHOOSE= and STOP= options are both set to SBC.
Output 14.1.1: Model Information
Output 14.1.2, Output 14.1.3, and Output 14.1.4 display the selected effects and the parameter estimates for 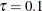 ,
, 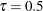 , and
, and 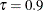 , respectively. You can see that the forward selection method correctly selects active effects for all three quantile levels.
, respectively. You can see that the forward selection method correctly selects active effects for all three quantile levels.
Output 14.1.2: Parameter Estimates at 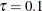
| Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standardized Estimate |
Standard Error |
95% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | 0.01179 | 0 | 0.01192 | -0.01158 | 0.03516 | 0.99 | 0.3225 |
| x2 | 1 | -0.22871 | -0.21829 | 0.00946 | -0.24725 | -0.21017 | -24.19 | <.0001 |
| x3 | 1 | -1.37991 | -0.78452 | 0.01556 | -1.41042 | -1.34939 | -88.67 | <.0001 |
Output 14.1.3: Parameter Estimates at 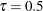
Output 14.1.4: Parameter Estimates at